the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Seasonal flow forecasting in Africa; exploratory studies for large lakes
Kevin Sene
Wlodek Tych
For many applications, it would be extremely useful to have insights into river flows at timescales of a few weeks to months ahead. However, seasonal predictions of this type are necessarily probabilistic which raises challenges both in generating forecasts and their interpretation. Despite this, an increasing number of studies have shown promising results and this is an active area for research. In this paper, we discuss insights gained from previous studies using a novel combined water balance and data-driven approach for two of Africa's largest lakes, Lake Victoria and Lake Malawi. Factors which increased predictability included the unusually long hydrological response times and statistically significant links to ocean-atmosphere processes such as the Indian Ocean Dipole. Other lessons learned included the benefits of data assimilation and the need for care in the choice of performance metrics.
- Article
(866 KB) - Full-text XML
- BibTeX
- EndNote
Seasonal river flow forecasts aim to provide useful information for operations and planning from weeks to months ahead. Potential applications include water supply planning, hydropower generation and irrigation scheduling. This is a developing area both in terms of the technical approaches used and interpretation of the outputs provided.
The forecasting techniques potentially available include statistical approaches, ensemble streamflow prediction, and the direct input of ensemble rainfall forecasts into hydrological models. However, forecast skill depends on several factors, including seasonal influences and the catchment size, location and antecedent conditions (e.g. Greuell et al., 2019; Mendoza et al., 2017; Robertson and Wang, 2012; Sene, 2016). Often a key challenge is that the required forecast lead times exceed hydrological response times, requiring a greater reliance on long-range rainfall forecasts, with the many uncertainties that entails.
One situation which can improve predictability is when there is considerable storage in a catchment, such as from snowpack, groundwater or large lakes and reservoirs. The Rift Valley lakes of east and southern Africa provide one such example, and due to their huge size, offer considerable potential for deriving seasonal forecasts over operationally useful timescales.
Here we describe insights gained from previous studies by the authors into two of Africa's largest lakes, Lake Victoria and Lake Malawi. These flow into the White Nile and Shire River respectively. A novel water balance and statistical approach was used, building on stochastic transfer function modelling techniques previously applied in a wide range of environmental applications (e.g. Young, 2011; Tych and Young, 2012). The approaches used are only briefly outlined here, but are described in more detail in Sene et al. (2017, 2018) and Sene and Tych (2018).
In contrast, most previous studies have focussed on developing statistical links between river flows and external drivers such as climate indices. For example, Siam and Eltahir (2015) describe a Bayesian model for the Nile incorporating Indian and Pacific Ocean climate indices, while Elganiny and Eldwer (2018) used Artificial Neural Network and ARMA approaches. Gehad et al. (2017) have also compared forecast skill with ensemble approaches for the Blue Nile. For the Shire River, Jury and Gwazantini (2002) describe a seasonal forecasting model for Lake Malawi using a statistical model including climate indices, and Jury (2014) describes a detailed statistical analysis of links between climate and hydrology using atmospheric model reanalyses and satellite data.
In this paper, other topics discussed include the potential for real-time updating of model outputs using techniques similar to those used in real-time flood forecasting, and the choice of performance metrics to deal with a statistically non-stationary response over timescales of months or more. An analytical approach also provided useful insights. Finally, some priorities for future research are considered in this challenging area, including the prospects for seasonal forecasting for smaller lakes and river basins.
2.1 The study area
Lake Victoria lies on the equator and its catchment spans six countries: Burundi, the Democratic Republic of the Congo, Kenya, Rwanda, Tanzania and Uganda (Fig. 1). It plays an important role in hydropower generation, irrigation and water supply in the region. The lake has some of the longest hydrological records in Africa starting with routine observations of levels in the 1890s and rainfall a decade later, albeit initially with a sparse network of rain gauges. Regular observations of outflows began in the 1940s, and flows have been regulated for hydropower production since 1953. The lake is the largest in Africa with surface and catchment areas of about 68 000 and 194 000 km2.
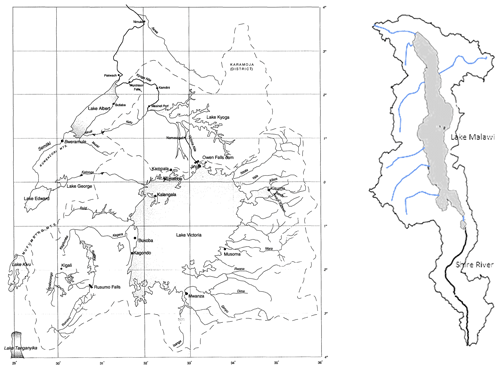
Figure 1Map of the Lake Victoria region (Source: IAHS Press and Sutcliffe and Parks, 1999) (left) and Lake Malawi (right).
Lake Malawi, also shown in Fig. 1, lies several hundred kilometres to the south and its catchment is mainly in Malawi and Tanzania, with a smaller contribution from Mozambique. Level observations also began in the 1890s with regular outflow observations since 1948. The lake has been regulated for hydropower production since 1965. Its surface and catchment areas are about 28 750 and 95 570 km2.
For both lakes, regional rainfall is affected by the annual passage of the Intertropical Convergence Zone (ITCZ). For Lake Victoria, this results in two main rainfall seasons, which are typically between March and May and October and December. In contrast, Lake Malawi lies near the southernmost end of ITCZ excursions and much of the catchment experiences a single main rainfall season from November to April or May.
The datasets used for these studies are described in Sene et al. (2017, 2018) and included rainfall, lake level and lake outflow records. To provide the best possible data coverage, extensive use was made of previously validated and infilled values, many of which themselves relied on observations and record extension techniques developed during an unusually intensive period of monitoring in the 1970s and 1980s (WMO, 1982, 1983). This meant that monthly data availability and completeness was particularly good and allowed the focus to be on issues related to model structure and performance, rather than trying to resolve issues due to sparse data. Nevertheless, the records included some of the most extreme flood and drought periods on record. The periods chosen for analysis were 1925 to 1990 for Lake Victoria and 1954 to 1980 for Lake Malawi.
Several climate indices were considered for use in the analyses. Exploratory work typically suggested a weak correspondence with rainfall for El Niño indices at lag times of a few months and a rather stronger correspondence with an index for the Indian Ocean Dipole. Based on these studies, the indices chosen for use in the simulations were NINO34 (Trenberth, 1997) and JAMSTEC's estimates for the Dipole Model Index (DMI) and illustrative results are discussed later. More detailed studies into links to global and regional climate typically suggest lag times of about two months for Shire River flows (Jury, 2014) and values up to several months for east Africa at a seasonal timescale (Nicholson, 2017), although there are many factors and variables to consider when interpreting these findings.
2.2 Simulation techniques
The studies used an innovative approach to estimating lake outflows, based on a combination of water balance and transfer function techniques. Only brief details are given here while the full methodology is described in Sene et al. (2017, 2018).
The starting point for the analyses was the water balance for a lake, which can be expressed as:
where h is the water level, N is the net inflow, Qo is the outflow, A is the surface area, and t is time. Based on previous studies (e.g. Piper et al., 1986) the lake areas were assumed to be constant and the lake outflows were estimated from an equation of the form Qo=ahb.
The net inflow is normally expressed in the following form:
where P and E are the lake rainfall and evaporation and Qi is the tributary inflow. Any additional terms which are difficult to measure or estimate, such as groundwater seepage, were considered to contribute to the overall model uncertainty.
To simulate the water balance, a data-driven stochastic framework was adopted which has proven useful in many other environmental applications, such as real-time flood forecasting and assessing the long-term variability in climate records (Beven, 2009; Young, 2013). Some advantages of this approach are that few assumptions are required about the statistical characteristics of the datasets used and the relationships between them, and that estimates for the uncertainty in model outputs are intrinsic to the approach.
A transfer function solution was sought, inspired by the observation by Young (2011) that for the linear case (b=1) Eq. (1) can be solved in this form without further approximation. The following more generalised form was adopted, allowing for both serial dependence in model inputs and the influence of external variables (ut), such as climate drivers:
Here, A, B, C and D are polynomial functions and z−1 is the backward shift operator .
The parameter values were estimated using a stochastic recursive estimation approach, which also provides estimates for the uncertainty in parameter values and how they vary over time. Tych and Young (2012) and Young (2013) provide more details.
2.3 Results and discussion
Similar techniques were applied to both Lake Victoria and Lake Malawi and, again, the results are described in detail in Sene et al. (2017, 2018). Here we draw out some key insights which may be relevant to future studies of these two lakes and to other large lakes in Africa.
2.3.1 Net inflows
The net inflows were estimated from the outflow terms in Eq. (2) since, in principle, lake levels and outflows can be measured and infilled with greater precision than the lake rainfall and tributary inflows. This approach has been widely used in previous studies (e.g. Piper et al., 1986) and avoided the need to estimate the individual inflow terms for which there can often be many uncertainties, particularly when as here catchments are large and monitoring networks are sparse. As a further refinement, values were expressed in standardised form to focus on the underlying climate signals, thereby helping to reduce the influence of bias in observations.
For Lake Victoria, cross correlation analyses suggested that r2 coefficients with lake rainfall were highest (> 0.8) for no time delay but still statistically significant with a 1 month delay, whilst autocorrelation coefficients were highest for a 1 month delay. This provides an indication of the potential forecasting lead times for net inflow from rainfall variability alone whilst, in contrast, linkages with tributary inflows were considerably less. Similar results were obtained for Lake Malawi and helped to inform the overall structure of the model in Eq. (3).
2.3.2 Data assimilation
When forecasting river flows at short timescales, such as in real-time flood forecasting, one widely used approach is to update model outputs based on telemetry data. This approach is called data assimilation and is effective over timescales comparable with the hydrological response time of a catchment. Clearly, this is unlikely to be the case in many seasonal forecasting applications, but for a large lake like Lake Victoria, given the huge storage influences it is potentially an option, and the use of this approach was a novel aspect of these studies. Various formulations were explored for the assimilation component, including an error prediction approach and multiple regression models for the forecast model residuals.
The best forecast skill was obtained by incorporating both El Niño and Indian Ocean Dipole indices into the regression models at lag times of 5–7 months for Lake Victoria, and 6–9 months and 3–5 months respectively for Lake Malawi. This gave better forecast skill than the more usual approach of developing statistical relationships between rainfall and climate indices. In contrast, an Autoregressive Regressive Moving Average (ARMA) approach for the residuals alone only provided benefits at lead times of 2–3 months.
2.3.3 Performance metrics
The data assimilation studies highlighted another important issue, which was the choice of performance metrics to use.
The reason for this was that, for large lakes such as Lake Victoria and Lake Malawi, one characteristic of the lake level and outflow series is that, due to the huge storage, there can be underlying longer term influences superimposed on the daily and seasonal variations due to rainfall. This non-stationary response requires special consideration and for this study it was considered most important to focus on the annual peaks in levels and outflows.
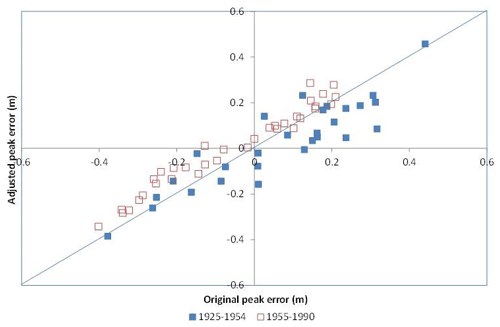
Figure 2 shows an example of this type of output, showing the improvements in peak level estimates when climate indices were included in the data assimilation component. This example was for Lake Victoria and in future studies, a further refinement would be to consider the timing errors in peaks as well. Many other measures could be considered and this is a worthwhile area for future research.
2.3.4 Analytical approaches
In some hydrological situations, an analytical approach can also give useful insights, and for a lake it is possible to solve Eq. (1) analytically for some integer values of b in the outflow term.
These analyses provided some useful additional insights into the key timescales for lake response; for example, suggesting that, following a sudden increase in net inflows, such as during heavy rainfall, for both lakes an approximately exponential decay in levels might be expected over timescales of 4–5 years, if inflows revert to their long-term mean values.
This provided further evidence of a non-stationary response, and an indication of lake response times due to storage, albeit for a highly idealized situation. Similar idealized solutions might be sought in other seasonal forecasting applications although normally, of course, a numerical solution is required for further insights.
2.4 Conclusions
This study has highlighted some methodological issues arising from exploratory studies into seasonal flow forecasting using a data-driven approach. Some issues to consider in developing models for other lakes include the potential role of climate indices in data assimilation, the choice of suitable performance metrics and the value of simple analytical solutions to explore the response.
Future studies might also consider the forecast skill gained from including seasonal rainfall and air temperature forecasts as model inputs for comparison with an ensemble streamflow prediction approach. The use of spatially varying (grid-based) climate indices might also be considered and, for smaller lakes, more consideration given to the spatial relationships between tributary inflows, perhaps at a daily time step. The modelling framework described here might also be developed further using a so-called State Dependent Parameter approach to integrate the dynamic input-output model and data assimilation components into a single modelling framework, using a unified State Space form and estimated (forecast) using Kalman Filter tools.
One key objective of studies such as these is to develop techniques that could be used operationally. For large lakes, perhaps the longest-established systems are for the Great Lakes in the USA and Canada. These combine empirical and physically based models, with precipitation and air temperature outlooks and ensemble forecasts (Gronewold et al., 2011; Bolinger et al., 2017). A Nile Basin Flow Forecasting System is also at the planning stage and the Eastern Nile Technical Regional Office (ENTRO) issues a Flood Preparedness and Early Warning Bulletin during the flood season, based on short to medium-range meteorological forecasts. The WMO Hydrological Status and Outlooks (HydroSOS) initiative (http://www.wmo.int, last access: 4 November 2021) is also considering Lake Victoria.
No data sets were used in this article.
This paper draws on previous research by the authors on seasonal flow forecasting using modelling techniques developed jointly by the two co-authors (KS, WT), making use of a software framework described in Tych and Young (2012). The manuscript was prepared by KS with expert contributions from WT.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “Hydrology of Large River Basins of Africa”. It is a result of the 4th International Conference on the “Hydrology of the Great Rivers of Africa”, Cotonou, Benin, 13–20 November 2021.
We would like to thank the Centre for Ecology and Hydrology for permission to use the datasets for Lake Victoria referred to in this paper; also Michael Kizza for providing additional independently derived records for comparison. The WMO (1983) study was led by Chris Kidd and provides a valued contribution to understanding of the hydrology of Lake Malawi.
Beven, K.: Environmental Modelling: An Uncertain Future?, CRC Press, UK, 2009.
Bolinger, R. A., Gronewold, A. D., Kompoltowicz, K., and Fry, L. M.: Application of the NMME in the development of a new Regional Seasonal Climate Forecast Tool, B. Am. Meteorol. Soc., 2017, 555–564, 2017.
Elganiny, M. and Eldwer, A.: Enhancing the Forecasting of Monthly Streamflow in the Main Key Stations of the River Nile Basin, Water Resour., 45, 660–671, 2018.
Gehad, N., Doaa, A., Shokry, A., and Tahani, Y.: Flow forecasting and skill assessment in the Blue Nile Basin, Nile Water Sci. Eng. J., 10, 29–37, 2017.
Gronewold, A. D., Clites, A. H., Hunter, T. S., and Stow, C. A.: An appraisal of the Great Lakes advanced hydrologic prediction system, J. Great Lakes Res., 37, 577–583, 2011.
Greuell, W., Franssen, W. H. P., and Hutjes, R. W. A.: Seasonal streamflow forecasts for Europe – Part 2: Sources of skill, Hydrol. Earth Syst. Sci., 23, 371–391, https://doi.org/10.5194/hess-23-371-2019, 2019.
Jury, M. R.: Malawi's Shire River Fluctuations and Climate, J. Hydrometeorol., 15, 2039–2049, 2014.
Jury, M. R. and Gwazantini, M. E.: Climate variability in Malawi, part 2: sensitivity and prediction of lake levels, Int. J. Climatol., 22, 1303–1312, 2002.
Mendoza, P. A., Wood, A. W., Clark, E., Rothwell, E., Clark, M. P., Nijssen, B., Brekke, L. D., and Arnold, J. R.: An intercomparison of approaches for improving operational seasonal streamflow forecasts, Hydrol. Earth Syst. Sci., 21, 3915–3935, https://doi.org/10.5194/hess-21-3915-2017, 2017.
Nicholson, S. E.: Climate and climatic variability of rainfall over eastern Africa, Rev. Geophys., 55, 590–635, https://doi.org/10.1002/2016RG000544, 2017.
Piper, B. S., Plinston, D. T., and Sutcliffe, J. V.: The water balance of Lake Victoria, Hydrolog. Sci. J., 31, 25–37, 1986.
Robertson, D. E. and Wang, Q. J.: A Bayesian Approach to Predictor Selection for Seasonal Streamflow Forecasting, J. Hydrometeorol., 13, 155–171, 2012.
Sene, K.: Hydrometeorology: Forecasting and Applications, 2nd Edn., Springer, Dordrecht, 427 pp., 2016.
Sene, K. and Tych, W.: Some challenges in seasonal forecasting for large lakes and reservoirs, Seasonal Forecasting: Meeting User Needs, British Hydrological Society National Meeting, Loughborough, UK, 2018.
Sene, K., Piper, B., Wykeham, D., McSweeney, R., Tych, W., and Beven, K.: Long-term variations in the net inflow record for Lake Malawi, Hydrol. Res., 48, 851–866, 2017.
Sene, K., Tych, W., and Beven, K.: Exploratory studies into seasonal flow forecasting potential for large lakes, Hydrol. Earth Syst. Sci., 22, 127–141, https://doi.org/10.5194/hess-22-127-2018, 2018.
Siam, M. S. and Eltahir, E. A. B.: Explaining and forecasting interannual variability in the flow of the Nile River, Hydrol. Earth Syst. Sci., 19, 1181–1192, https://doi.org/10.5194/hess-19-1181-2015, 2015.
Sutcliffe, J. V. and Parks, Y. P.: The Hydrology of the Nile, IAHS Special Publication no. 5, IAHS Press, Wallingford, ISBN 978-1-901502-75-6, 192 pp., 1999.
Trenberth, K. E.: The Definition of El Niño, B. Am. Meteorol. Soc., 78, 2771–2777, 1997.
Tych, W. and Young, P. C.: A Matlab software framework for dynamic model emulation, Environ. Model. Softw., 34, 19–29, 2012.
WMO: Hydrometeorological Survey of the Catchments of Lake Victoria, Kyoga and Mobutu Sese Seko, WMO Report, 1982.
WMO: A Water Resources Evaluation of Lake Malawi and the Shire River, WMO Report No. MLW/77/012, 1983.
Young, P. C.: Recursive Estimation and Time-Series Analysis: An introduction for the student and practitioner, 2nd Edn., Springer, 2011.
Young, P. C.: Hypothetico-inductive data-based mechanistic modeling of hydrological systems, Water Resour. Res., 49, 915–935, 2013.