Estimating extreme dry spell risk in Ichkeul Lake Basin (Northern Tunisia): a comparative analysis of annual maxima series with a Gumbel distribution

This paper analyses a 42 year time series of daily precipitation in Ichkeul Lake Basin (northern Tunisia) in order to predict extreme dry-spell risk. Dry events are considered as a sequence of dry days separated by rainfall events from each other. Thus the rainy season is defined as a series of rainfall and subsequent dry events. Rainfall events are defined as the uninterrupted sequence of rainy days, when at last on one day more than a threshold amount of rainfall has been observed. A comparison of observed and estimated maximum dry events (42 year return period) showed that Gumbel distribution fitted to annual maximum series gives better results than the exponential (E) distribution combined with partial duration series (PDS). Indeed, the classical Gumbel approach slightly underestimated the empirical duration of dry events. The AMS–G approach was successfully applied in the study of extreme hydro-climatic variable values. The results reported here could be applied in estimating climatic drought risks in other geographical areas.

1 Introduction

A proper simulation of precipitation is important. Precipitation is a very important element of climate that affects both the natural environment and human society. Events ranging from prolonged droughts to short-term, high intensity floods are often associated with devastating impacts both to society and the environment (Hui et al., 2005). An alternative to the Markov chain process which is typically used to simulate the occurrence of precipitation is to use a wet-dry spell model or alternating renewal model, that is, to simulate wet and dry spells separately by fitting their durations to an appropriate probability distribution. Among the study using the wet-dry spell approach one can cite, for example, Bogardi and Duckstein (1993); Wilks (1999); Mathlouthi (2009); Mathlouthi and Lebdi (2008, 2009, 2017); Dunxian et al. (2015); Konjit et al., 2016.

It is well known that dry spells cause major economic and human losses, and numerous studies have highlighted the need for drought prevention and mitigation plans (Vicente-Serrano and Beguería, 2003). The spatial and temporal assessment of dry spells is necessary in order to protect agriculture, water resources and other socio economic concerns, and areas at risk from droughts of long duration and great intensity need to be determined. Sivakumar (1992) point up the importance of admitting partial patterns of extreme drought, which can then be used in the management of cultivated areas (crop selection, irrigation planning, etc.) and water resources management.

The analysis of extremes in dry-spell series has been examined classically using annual maximum series (AMS) adjusted to a Gumbel distribution (Gupta and Duckstein, 1975; Lana and Burgueño, 1998). The AMS are constructed by determining the maximum dry spell for each year, so the series length equals the number of years for which records are available. However, the main drawback is the loss of the second, third, etc. largest annual dry spells, which might exceed the maximum dry spells of other years. An option approach is the partial duration series (PDS), which is constructed using the values above a selected threshold regardless of the year in which they occurred (Hershfield, 1973; Vicente-Serrano and Beguería, 2003). Typically, the generalized Pareto (GP) distribution has been used to model PDS (Bobée and Rasmussen, 1995). Although the PDS approach has obvious advantages over the AMS approach (Cunnane, 1973), it has been used only infrequently in precipitation dry-spell analysis (Vicente-Serrano and Beguería, 2003).

In virtue, this paper is focused on the modelling of rainfall occurrences under Mediterranean climate by wet-dry spell approach. The intended objective is to determine whether the use of AMS with the Gumbel distribution (AMS–G approach) is suitable for modelling extreme dry-spell risk; to analyse if PDS with a probability distribution, that best fits the data set, is adequate for modelling extreme dry-spell risk and finally to compare both approaches with the observed maximum dry spells to determine the most suitable estimation of drought risk.

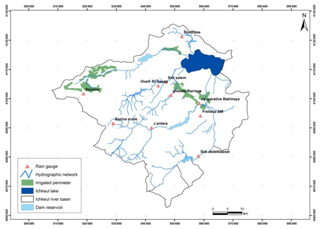
The study area is the Ichkeul basin (Northern Tunisia) with several dams for irrigation, drinking water and water transfer to other regions of the country. The precipitation irregularity and the frequent dry spells are major restrictive factors in crop growth and water demand satisfaction imposed on dams. For this reason, this area is particularly suitable for examining this approach.

2 Data

Daily precipitation records at rain gauges in the basin of Ichkeul Lake located in Northern Tunisia were used in this analysis (Fig. 1). The total area of this region calculated by GIS is 2120 km². The rainy season starting at September and lasting until the beginning of May. The mean of annual rainfall is 600 mm; the coefficient of variation is 0.25. The climate of this area is classified as sub-humid; the average annual rainfall is below 40 % of the total annual potential evaporation. Except in occasional wet years, most precipitation is confined to the winter months in this basin. The dry season lasts from May to August. Daily values of precipitation are quite variable. There is also considerable variation from year to year. Ten time series of daily precipitation exist for the period from 1968 to 2010.

Figure 1 Study area.

3 Method

3.1 Extract series of dry and rainfall events

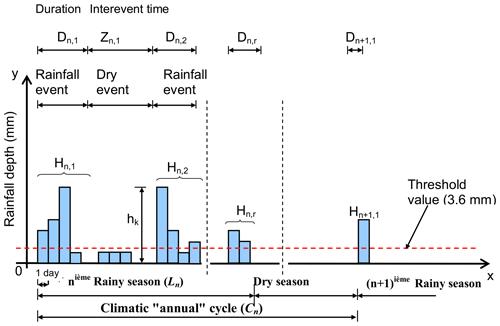
In the wet-dry spell approach, the time-axis is split up into intervals called wet periods and dry periods. A rainfall event is an uninterrupted sequence of wets periods. The definition of event is associated with a rainfall threshold value which defines wet (Fig. 2). As this limit 3.6 mm d⁻¹ has been selected. This amount of water corresponds to the expected daily evapotranspiration rate, marking the lowest physical limit for considering rainfall that may produce utilizable surface water resources. In this approach, the process of rainfall occurrences is specified by the probability laws of the length of the wet periods, and the length of the dry periods (time between storms or inter-event time).

Figure 2 Event representation of the climatic cycle.

The rainfall event r in a given rainy season n will be characterized by its duration D_n,r, the temporal position within the rainy season, the dry event or inter-event time Z_n,r and by the cumulative rainfall amounts of H_n,r of D_n,r rainy days (Fig. 2).

$$\begin{array}{}\text{(1)}& r=f(D_{n,r},H_{n,r},Z_{n,r})\end{array}$$

Where f is the function defined on $R_{+}^{\ast }$, which to each event r associates a value D, H and Z themselves, real discrete random variables.

$$\begin{array}{}\text{(2)}& {\displaystyle }{Z}_{n,r}=x_{n,r}-x_{n,r-\mathrm{1}}\text{(3)}& {\displaystyle }{H}_{n,r}=\sum _{k=\mathrm{1}}^{D_{n,r}}{h}_k\end{array}$$

Where h_k represents the total daily rainfall in mm. Let h_k>0 and at least a value of h_k>3.6 mm.

The varying duration of the events requires that the cumulative rainfall amounts corresponding to each event should be conditioned by the duration of the event. The identification and fitting of conditional probability distributions to rainfall amounts may be problem especially in the case of short records and for events with extreme (long) durations (Foufoula-Georgiou and Georgakakos, 1991). The number of rainfall events per rainy season n is N_n and the length L_n of this last, of random duration, is defined as the time span between the start of the first and the end of the last rainfall event.

$$\begin{array}{}\text{(4)}& L_n=\sum _{r=\mathrm{1}}^{N_n}{D}_{n,r}+\sum _{r=\mathrm{1}}^{N_n-\mathrm{1}}{Z}_{n,r}\end{array}$$

The length of the climatic cycle C_n is determined as the time lapsed between the onsets of two subsequent rainy seasons.

$$\begin{array}{}\text{(5)}& C_n=x_{n+\mathrm{1},r_{\mathrm{1}}-}{x}_{n,r_{\mathrm{1}}}\end{array}$$

3.2 Extreme dry event modelling with annual maximum series and Gumbel distribution

The distribution introduced by Gumbel is very useful for extreme dry event frequency modelling using the AMS–G approach (Gumbel, 1958; Vicente-Serrano and Beguería-Portugués, 2003). The Gumbel distribution is a two-parameter distribution with constant skewness. It is a particular case of the three-parameter generalized extreme value (GEV) distribution, i.e. the limit distribution for maxima series. The Gumbel is usually preferred to the GEV because of its ease of calculation. Its probability density function is

$$\begin{array}{}\text{(6)}& f\left(x\right)={\displaystyle \frac{\mathrm{1}}{\propto }}{e}^{{\left\{-\left[\left(x-\mathit{\beta }\right)/\mathit{\alpha }\right]\right\}}^{-e^{\left\{-\left[\left(x-\mathit{\beta }\right)/\mathit{\alpha }\right]\right\}}}}\end{array}$$

and its cumulative distribution function is expressed by

$$\begin{array}{}\text{(7)}& F\left(x\right)=e^{-e^{-\left[\frac{x-\mathit{\beta }}{\mathit{\alpha }}\right]}}\end{array}$$

where x is the value of the variable, and α and β are scale and location parameters of the distribution, respectively. The mean and the variance are $\mathit{\mu }=\mathit{\beta }+\mathrm{0.5772}\mathit{\alpha }$ and ${\mathit{\sigma }}^{\mathrm{2}}=\frac{{\mathit{\pi }}^{\mathrm{2}}{\mathit{\alpha }}^{\mathrm{2}}}{\mathrm{6}}$, accordingly.

The prospective maximum dry event for a T year period X_T can be calculated using

$$\begin{array}{}\text{(8)}& X_T=\mathit{\beta }-\mathit{\alpha }\ln \left\{-\ln \left[\mathrm{1}-\left(\mathrm{1}/T\right)\right]\right\}\end{array}$$

3.3 Estimation of extreme dry event using PDS

3.3.1 Characteristics of PDS

Although the preceding method has been widely used in the study of extreme dry spells, in the analysis of other hydrological and climatic variables (e.g. extreme rainfall, floods) many studies prefer to use PDS or series of peaks over an upper limit. Given the dry spell series $a=\mathit{\{}{a}_{\mathrm{1}},a_{\mathrm{2}},\mathrm{\dots },a_n\mathit{\}}$, for the station a, where a_i is the duration of a given dry spell, the PDS $b=\mathit{\{}{b}_{\mathrm{1}},b_{\mathrm{2}},\mathrm{\dots },b_j\mathit{\}}$ consists of all the values of the original series that exceed a predetermined upper limit a₀:

$$\begin{array}{}\text{(9)}& b_j=a_i-a_{\mathrm{0}}\forall a_i>a_{\mathrm{0}}\end{array}$$

The size of the series obtained depends, therefore, on the upper limit a₀. For this reason, PDS use the information contained in the original sample more efficiently, and permit the inclusion of more than one event per year, if they satisfy the conditions established in defining an extreme event (Chow et al., 1988; Vicente-Serrano and Beguería-Portugués, 2003).

3.3.2 Probability distributions used to adjust PDS

Many probability distributions have been adjusted to PDS hydrological series, including lognormal, Pearson III, Gamma, GEV, Weibull, etc. (Bobée et al., 1993; Vicente-Serrano and Beguería-Portugués, 2003). In this study, we evaluated the continuous probability distributions given by Hyfran software, and we found that the Exponential law is the best fitting probability distribution to PDS. The parameter estimates is performed by the method of moments. A Chi-Squared goodness-of-fit Test is used to determine how well the theoretical distribution fits the empirical distribution obtained from the sample data. The exponential (E) distribution function is

$$\begin{array}{}\text{(10)}& f\left(t\right)=b\cdot e^{-b(t-m)}m<t<+\mathrm{\infty }\end{array}$$

where b parameter of the exponential distribution, can be estimated as the reciprocal mean $\stackrel{\mathrm{‾}}{t}$ of the sample of times observed:

$$\begin{array}{}\text{(11)}& b={\displaystyle \frac{\mathrm{1}}{\stackrel{\mathrm{‾}}{t}}}\end{array}$$

and its cumulative distribution function is expressed by

$$\begin{array}{}\text{(12)}& G\left(t\right)=\mathrm{1}-e^{-b(t-m)}m<t<+\mathrm{\infty }\end{array}$$

The event X_T in a period of T years is obtained using

$$\begin{array}{}\text{(13)}& X_T=m-{\displaystyle \frac{\mathrm{1}}{b}}\ln \left(\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{T}}\right)\end{array}$$

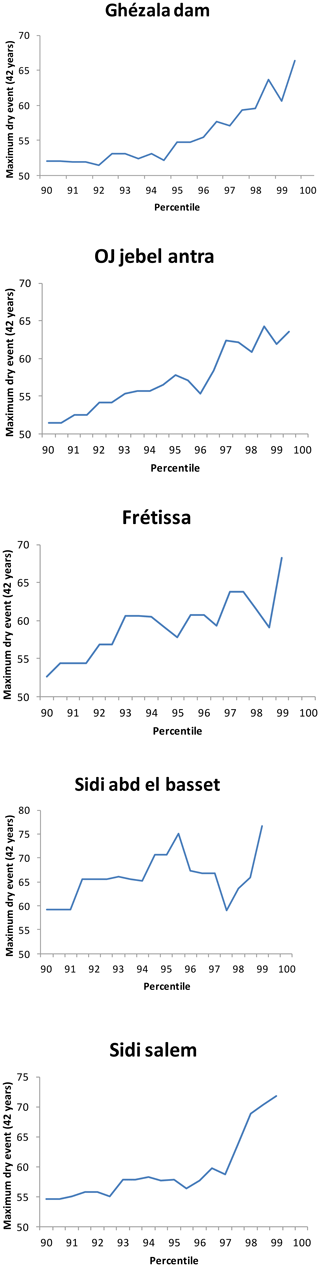
A major problem in using PDS is the selection of the lower bound a₀. This value should be low enough to ensure the inclusion of as much relevant information as possible, without violating the assumption of independence of the peaks. Various methods have been proposed to determine the most appropriate lower bound (Ashkar and Rouselle, 1987; Madsen et al., 1997). However, according to Vicente-Serrano and Beguería-Portugués (2003) Beguería (2003) has shown that the parameters and quantile estimations vary randomly with the threshold value, and no single value is entirely adequate. For this reason, in this paper, the maximum dry event in the 42 year period was calculated using different lower bounds in the PDS–E approach. These bounds were defined using the percentiles of the dry event series every 0.5 from percentiles 90 to 99.5. Dry event were considered extreme above the 90th percentile.

3.4 Comparison of the AMS–G and PDS–E approaches

The maximum dry event observed in each series in the period 1968–2010 was extracted. These were compared with the 42 year estimates using the AMS–G and PDS–E approaches. It is clear that the maximum dry event observed in a 42 year period does not necessarily correspond to a return period of 42 years. This limitation was partially overcome by using several rain gauges in the same region. The goodness of fit was tested by means of the root-mean-square error (RMSE) (Willmott, 1982), the lowest value indicating the best estimation:

$$\begin{array}{}\text{(14)}& \text{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n{\left(z_i-{\widehat{z}}_i\right)}^{\mathrm{2}}}\end{array}$$

Where z_i is the observed value and ${\widehat{z}}_i$ the estimated value using annual maximum or partial duration series; n is the number of rain gauges.

4 Results

4.1 Selection of the lower bound in using PDS

The main problem in using PDS involves the selection of the lower bound. In theory, the method is invariant to the variation in the lower bound. In practice, however, the results may vary greatly, especially with the sample sizes that are common in hydro climatic studies. This is exemplified in Fig. 3, in which the maximum dry spells expected in 42 years are shown for five rain gauges, in relation to the lower bound used. Whereas this value was expected to be similar independently of the lower bound chosen, it showed great random variation, being as 21 % compared to the average in some cases. Here, we assumed that the average of the different values would provide a good estimate of the unknown true value, this being less uncertain than using a unique, arbitrary, threshold.

Figure 3 Oscillation of the maximum dry event (days) estimations as a function of the selected percentile in the creation of the dry event PDS. Five representative rain gauges are shown.

4.2 Comparison of maximum dry event estimations using the AMS–G and PDS–E approaches with the observed maximum dry event

Figures 4 and 5 compare AMS–G and PDS–E estimates with the observed maximum dry events. The AMS–G method estimated adequately in the majority of cases the duration of the observed maximum dry events. The underestimation did not exceed 9 d, which prudent use of this method. The PDS–E clearly overestimated the maximum dry events duration. The difference between predicted and observed values varies from −5.4 % to 25.7 %.

The RMSE between the observed and estimated values is also highly indicative of the better performance of the AMS–G distribution. There was a better adjustment for the dry event series (RMSE = 4.7 versus 9.2).

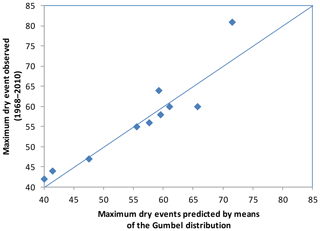
Figure 4 Differences between maximum dry events observed and estimated using AMS modelled using Gumbel distribution.

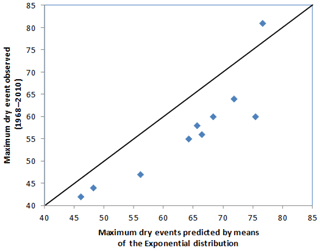
Figure 5 Differences between maximum dry events observed and estimated using PDS modelled using the Exponential distribution.

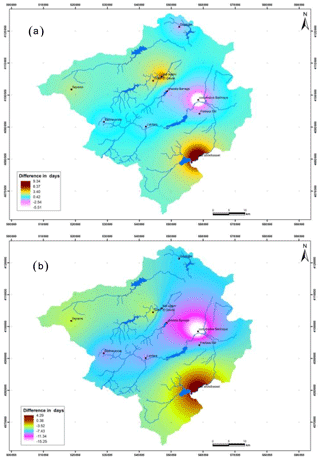
Figure 6 shows the spatial distribution of the maximum dry events observed in the study area between 1968 and 2010, along with the estimations using the PDS–E and AMS–G approaches. The longest dry events are located in the southern areas, with values over 81 consecutive days of precipitation below 3.6 mm. A negative southwestern gradient of the maximum dry event duration is established. The same pattern is revealed by both estimations. There were significant contrasts between the south and west, with differences about 40 d. The AMS–G map shows a much closer match to the observed data. The Exponential estimation is clearly little higher than the observed figure.

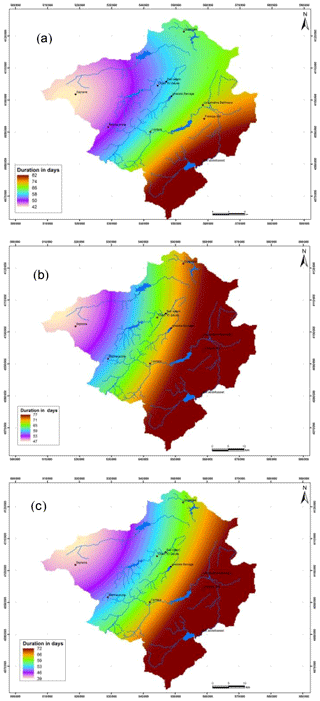
Figure 6 Maximum dry events: (a) observed in 42 years (1968–2010); (b) predicted using the E distribution; (c) predicted using Gumbel distribution.

The absolute errors of the estimations are shown in Fig. 7. The high magnitude of the errors resulting from the PDS–E approach is evident. Here, the positive errors indicate the underestimation provided by this approach. By contrast, the errors of the AMS–G approach include low negative values and the estimation is, in general, better.

Figure 7 Differences between maximum dry spells observed and estimated: (a) observed-estimated using Gumbel distribution; (b) observed-estimated using E distribution.

5 Discussion and conclusions

In this paper, we have used a PDS sampling in conjunction with an Exponential distribution. The results obtained have been compared with those obtained when adopting the AMS–G approach for the maximum dry event series observed in the study area.

Different probability distributions can be used to fit both AMS and PDS. The Gumbel distribution is a two parameter extreme values distribution widely used in modelling AMS. It has been compared with the one parameter Exponential distribution fitted to PDS. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution. It is obvious that a two parameter distribution would fit the observed data better than a one parameter one. Nevertheless, the need to estimate a greater number of parameters introduces an extra source of uncertainty that can affect the final estimates. Here, we find that the use of AMS-G is more efficient than PDS-E, contrary to what has been reported in several other studies. In this sense Moreno and Roldán (1999), Mkhandi et al. (2000) and Vicente-Serrano and Beguería (2003) indicated that the use of PDS for the stochastic modelling of extremes has yielded good results in the analysis of hydrological variables, whereas numerous studies have pointed out that AMS produces a significant loss of data for extreme modelling (Cunnane, 1973; Madsen et al., 1997; Vicente-Serrano and Beguería, 2003). Accordingly, the RMSE obtained by the AMS–G is lower than that obtained by the PDS–E when analysing the empirical maximum dry events for a 42 year time series.

One shortcoming of the PDS method is the selection of the upper limit used to define the PDS. We found that the final quantile estimates vary significantly when only small changes are made in the upper limit used. This result has been reported previously by the study of Vicente-Serrano and Beguería, 2003. To cope with this problem, as proposed by Vicente-Serrano and Beguería, (2003), the use of different upper limits when constructing a set of PDS, and then taking the average quantile estimates obtained with them. A set of PDS with limits ranging from percentiles 90 to 99.5, rising by 0.5 steps, was used in this paper. This proved to stabilize the variability of the quantile estimates. However, if this methodology is used on a more general scale, the upper limit range should be defined more precisely because it may differ for each set of data.

This paper has revealed that the widely used AMS–G approach estimates adequately the observed extreme dry-spell risk in the study area, by contrast with the PDS-E.

The results obtained here are of potential importance for agrarian planning. The method used is of potential importance for agrarian planning and of benefit in crop management. It facilitates the drawing of risk maps and the drafting of preventive and palliative plans for the mitigation of the effects of drought.