Application of Entrainment Velocity Concept for Evaluation of River Morphology: A Numerical Model Study

Conventionally, fine sediment transport is evaluated in terms of advection-diffusion equation of suspended sediment in which the erosion rate of sediment from the bedload layer plays a significant role. The present study aims to evaluate the riverbed evolution and associated morphological changes in fine sediment dominated Bhairab River of Bangladesh by a depth integrated two-dimensional numerical model. The erosion rate of bed sediment has been evaluated by two approaches. The first approach applies the fall velocity of the sediment particle and equilibrium reference sediment concentration. The other employs the entrainment velocity concept. The results obtained from numerical simulations are verified by the field investigations. The results suggest that the riverbed evolution and morphological changes predicted with the entrainment velocity concept show better agreement with the data obtained from the field investigations.

1 Introduction

Most of the riverbeds in Bangladesh are composed of fine-grained sediment that is easily entrained, slowly settled, remained in suspension, transported by flow over a long distance before settling and actively involved in the riverbed evolution and morphological changes. Many researchers such as Celik and Rodi (1988) have studied the mechanics of fine sediment transport and associated morphological changes taking the support of numerical model simulations. Depth-averaged equations comprised of governing equations for water flow, mass conservation for bedload and suspended sediment have been employed in these studies. The mass conservation of the suspended sediment is evaluated by advection–diffusion equation that contains erosion rate or sediment entrainment rate term and deposition rate term. The advection-diffusion equation for suspended sediment in non-equilibrium condition is as follows:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\displaystyle \frac{\partial ch}{\partial t}}& +{\displaystyle \frac{\partial cuh}{\partial x}}+{\displaystyle \frac{\partial cvh}{\partial y}}={\displaystyle \frac{\partial }{\partial x}}\left({\mathit{\epsilon }}_{x}h{\displaystyle \frac{\partial c}{\partial x}}\right)\\ & +{\displaystyle \frac{\partial }{\partial \mathrm{x}}}\left({\mathit{\epsilon }}_{y}h{\displaystyle \frac{\partial c}{\partial y}}\right)+E-D.\end{array}\end{array}$$

where c is the depth-averaged concentration of suspended sediment in the water column, h is the thickness of upper flow layer where sediment remain in suspension, u and v are the depth-averaged velocities in the x and ydirections, and ε_x and ε_y are the mixing coefficients in the x and y directions, E is the entrainment rate or erosion rate of the sediment from the bedload layer (hereinafter erosion rate term), D is the deposition rate of sediment from water column above the bedload layer.

Several formulas are available in literature for the erosion rate term emanating from the difference in the treatment of the sediment kinematics and the equilibrium reference sediment concentration (c_ae). Many researchers such as, Itakura and Kishi (1980), Van Rijn (1984, 1986), Garcia and Parker (1991) have proposed formulae for determining c_ae and computed erosion rate as E=c_aew₀, where w₀ is the fall velocity of the sediment particle. Garcia and Parker (1991) compared seven relations proposed by Einstein (1950), Engelund and Fredsoe (1976), Smith and McLean (1977), Itakura and Kishi (1980), Van Rijn (1984), Celik and Rodi (1984), Akiyama and Fukushima (1986) for entrainment rate of non-cohesive sediment into suspension and concluded that the relations proposed by van Rijn and Smith and McLean perform show better agreement against a common set of experimental data. Findings from investigations on the mechanics of suspended sediment-laden flow as well as data from the experimental and field observations have revealed that the conventional methods overestimate c_ae (Itakura and Kishi, 1980; Garcia and Parker, 1991). Harada et al. (2022) compared the equilibrium reference suspended sediment concentration obtained using the methods proposed by them and the formulas proposed by Van Rijn (1986), Itakura and Kishi (1980) and Garcia and Parker (1991). They found that the formula proposed by Van Rijn (1986), Itakura and Kishi (1980) and Garcia and Parker (1991) exhibit higher sediment concentration for sediment particles having $w_{\mathrm{0}}/u_{\ast }$ in the range of 0.01 to 0.1.

Noticeable deviations are noted among studies when c_ae from field observations and experimental investigations are plotted against $w_{\mathrm{0}}/u_{\ast }$ where, u_∗ is the shear velocity and defined as $u_{\ast }=\sqrt{gh{i}_{\mathrm{e}}}$ and i_e is the energy slope. Moreover, riverbed having sediment diameter several tens of micrometres and $w_{\mathrm{0}}/u_{\ast }$ falls out lower range, difficulties arise to apply c_ae chart and predicted erosion rates by the conventional formulae are relatively high (Harada and Egashira, 2020; Harada et al., 2022). Density stratification during the high flow conditions significantly affects the suspended sediment transport (Wright and Parker, 2004). The density stratification effects tend to be greater in large, low-slope rivers. To solve such difficulties, Harada and Egashira (2020) have introduced the entrainment velocity concept that rooted on the density stratified flows. They also have developed a method to evaluate erosion rate for very fine sediment and validated it by data from flume tests.

Bedload transport is crucial to maintain stable channel in sand bed rivers. Lateral diffusive transport of suspended sediment from the central region of the river increases the suspended sediment concentration besides deposition rate near the bank region. The deposited sediment returns to the central region as later bedload under the influence of gravity. A stable channel cross section is achieved when the lateral diffusive transport of suspended sediment is balanced by the lateral bedload (Parker, 1978; Ikeda and Izumi, 1991). Estimation of the bedload transport depend on the functional form of bedload transport rate formulae. Most of the usually applied formulae such as, formulae proposed by Meyer-Peter and Müller (1948), Ashida and Michiue (1972) can be expressed in terms of shear stress excess or its equivalent and have a functional form of ${\mathit{\tau }}_{\ast }^{\mathrm{1.5}}$ for high bed shear stress, here τ_∗ is the non-dimensional bed shear stress. Bedload rates using such formulae for high bed shear stress is independent of sediment size. There are bedload rate formulae with its functional form of ${\mathit{\tau }}_{\ast }^{\mathrm{2.5}}$ (e.g., Egashira et al., 1997) in which the bedload rates are contrariwise proportional to sediment particle size. Harada and Egashira (2020) has proposed the visco-coulomb model to evaluate bedload rates for very fine sediment which has been derived from the velocity profile in bedload layer and is expressed as follows:

$$\begin{array}{}\text{(2)}& q_{\mathrm{b}}={\displaystyle \frac{c_{\mathrm{s}}}{\mathrm{6}}}{\displaystyle \frac{u_{\ast }{h}_{\mathrm{s}}}{\mathit{\upsilon }}}{u}_{\ast }{h}_{\mathrm{s}}.\end{array}$$

where q_b is the bedload rate, c_s is the depth-averaged concentration of sediment in the bedload layer, h_s is the thickness of bedload layer, ν is the kinematic viscosity. The bedload layer thickness is expressed as follows:

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{h_{\mathrm{s}}}{h}}={\displaystyle \frac{\tan \mathit{\theta }}{\left(\mathit{\sigma }/\mathit{\rho }-\mathrm{1}\right)c_{\mathrm{s}}\tan \mathit{\varphi }}}.\end{array}$$

where tan θ is the bed slope that, under non-uniform flows slowly varying in space, can be replaced by energy slope, σ and ρ is the mass density of sediment and water respectively, ϕ is the angle of friction.

The present study aims to evaluate the riverbed evolution and associated morphological changes in a fine sediment-dominated Bhairab River of Bangladesh using a depth-averaged two-dimensional model. To do so, we have estimated the erosion rate by applying the entrainment velocity concept as well as by the conventional method. The bedload rates are evaluated by bedload formulae having functional form ${\mathit{\tau }}_{\ast }^{\mathrm{1.5}}$ and ${\mathit{\tau }}_{\ast }^{\mathrm{2.5}}$ as well as by the visco-coulomb model. Moreover, the applicability of newly proposed formula of erosion rate by Harada and Egashira (2020) is discussed comparing with existing formulae.

2 Characteristic of study area

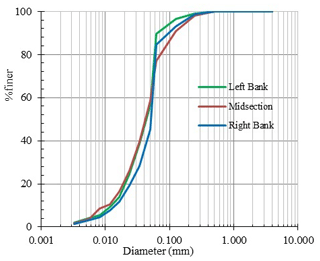
Bhairab River an alluvial meandering river is one of the right bank distributaries of the Ganges River that originates at Murshidabad district of West Bengal, India and enters into Bangladesh near Meherpur district. The total length within Bangladesh and average width is about 90 km and 60 m, respectively. The study reach is about 25 km long. Based on Landsat images from 1978 to 2016, bank lines of the Bhairab River have minor shifting tendency over the past thirty-eight years. Currently, Bhairab is disconnected from the Ganges River. Thus, the river is no more fed by the water and sediment from the Ganges River. The sediment load originates mainly from the riverbed which gives an opportunity to understand the entrainment rate of the fine sediment from the riverbed. Figure 1 shows that the downstream part of the river more meandering in nature comparing to the upstream part. The longitudinal bed slope of is 3.5 cm km⁻¹. The riverbed is composed of sediment having D₅₀=46 µm and average suspended sediment concentration varies from 50 to 70 mg L⁻¹. Figure 2shows that there are no significant changes in grain size distributions of riverbed and bank materials and thus between the floodplain and riverbed. In 2000, the river experienced maximum discharge of 140 m³ s⁻¹. However, minimum flow was found to be less than 1 m³ s⁻¹.

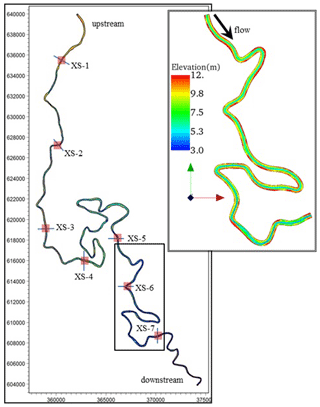
Figure 1 Planform of the part of Bhairab River within Bangladesh and elevation profile of study reach together with locations of the measured cross-sections.

Figure 2 Grain size distribution of bed and bank materials.

Table 1 Numerical simulations conditions adopted in the present study.

3 Governing equations for numerical model

To assess riverbed evolution and morphological changes, we have employed mass conservation equations for upper flow layer with suspended sediment, and for lower flow layer in which bedload dominates, besides the governing equations for the water flow. The governing equations are as follows:

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\partial h}{\partial t}}+{\displaystyle \frac{\partial \left(uh\right)}{\partial x}}+{\displaystyle \frac{\partial \left(vh\right)}{\partial y}}=\mathrm{0}.\text{(5)}& {\displaystyle }\begin{array}{rl}& {\displaystyle \frac{\partial \left(hu\right)}{\partial t}}+{\displaystyle \frac{\partial \left(huu\right)}{\partial x}}+{\displaystyle \frac{\partial \left(huv\right)}{\partial y}}+gh{\displaystyle \frac{\partial (h+z_{\mathrm{b}})}{\partial x}}\\ & +{\displaystyle \frac{{\mathit{\tau }}_x}{\mathit{\rho }}}-{\displaystyle \frac{\partial \left(h{\mathit{\sigma }}_{xx}\right)}{\partial x}}-{\displaystyle \frac{\partial \left(h{\mathit{\tau }}_{yx}\right)}{\partial y}}=\mathrm{0}.\end{array}\text{(6)}& {\displaystyle }\begin{array}{rl}& {\displaystyle \frac{\partial \left(hv\right)}{\partial t}}+{\displaystyle \frac{\partial \left(huv\right)}{\partial x}}+{\displaystyle \frac{\partial \left(hvv\right)}{\partial y}}+gh{\displaystyle \frac{\partial (h+z_{\mathrm{b}})}{\partial y}}\\ & +{\displaystyle \frac{{\mathit{\tau }}_y}{\mathit{\rho }}}-{\displaystyle \frac{\partial \left(h{\mathit{\tau }}_{xy}\right)}{\partial x}}-{\displaystyle \frac{\partial \left(h{\mathit{\sigma }}_{yy}\right)}{\partial y}}=\mathrm{0}.\end{array}\text{(7)}& {\displaystyle \frac{\partial z_{\mathrm{b}}}{\partial t}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{1}-\mathit{\lambda }}}\left({\displaystyle \frac{\partial q_{\mathrm{b}x}}{\partial x}}+{\displaystyle \frac{\partial q_{\mathrm{b}y}}{\partial y}}+E-D\right)=\mathrm{0}.\end{array}$$

where where, t is the time, x and y are the coordinate in flow direction and transverse to flow direction, g is the acceleration due to gravity, σ_xx, σ_yy, τ_xy and τ_yx are the depth-averaged Reynolds stresses, τ_x and τ_y are the x and y components of bed shear stress (τ_b), z_b is the river bed elevation, q_bx and q_by are the x and y components of the bedload rate (q_b), λ is the porosity. The bed shear stress and depth averaged Reynolds-stresses are evaluated by conventional method.

We have applied three methods: (a) conventional formula (Ashida and Michiue, 1972) (b) visco-coulomb formula (Harada and Egashira, 2020) and (c) Egashira et al. (1997) formula to evaluate the bedload rates. The erosion rate is evaluated by conventional method (Itakura and Kishi, 1980) as well as by entrainment velocity concept (Harada and Egashira, 2020). Equilibrium sediment concentration (c_e) and entrainment velocity (W_e) for the latter approach that rooted on density stratified flow and are expressed as follows:

$$\begin{array}{}\text{(8)}& {\displaystyle }{c}_{\mathrm{e}}={\displaystyle \frac{W_{\mathrm{e}}}{w_{\mathrm{0}}}}{c}_{\mathrm{s}},{\displaystyle \frac{W_{\mathrm{e}}}{u}}\left(=e\right)={\displaystyle \frac{K}{R_{i\ast }}},R_{i\ast }=\left({\displaystyle \frac{\mathit{\sigma }}{\mathit{\rho }}}-\mathrm{1}\right)c_{\mathrm{s}}{\displaystyle \frac{gh}{u^{\mathrm{2}}}}.\text{(9)}& {\displaystyle }\begin{array}{rl}{c}_{\mathrm{e}}& ={\displaystyle \frac{K}{w_{\mathrm{0}}/u_{\ast }}}\sqrt{{\displaystyle \frac{\mathrm{8}}{f}}}{\displaystyle \frac{\mathrm{1}}{\left(\mathit{\sigma }/\mathit{\rho }-\mathrm{1}\right)}}{\displaystyle \frac{u^{\mathrm{2}}}{gh}}=\\ & {\displaystyle \frac{K}{w_{\mathrm{0}}/u_{\ast }}}{\left({\displaystyle \frac{\mathrm{8}}{f}}\right)}^{\mathrm{3}/\mathrm{2}}{\displaystyle \frac{i_{\mathrm{e}}}{\left(\mathit{\sigma }/\mathit{\rho }-\mathrm{1}\right)}}.\end{array}\end{array}$$

where R_i∗ is the Richardson number, e is the entrainment coefficient, f is the Darcy–Weisbach friction factor that defined as $u/u_{\ast }=\sqrt{\mathrm{8}/f}$, $K=\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{3}}$ (Egashira and Ashida, 1980). Nays2dh solver (Asahi et al., 2013) with appropriate modifications is applied for conducting the numerical simulations with the help of International River Interface Cooperative (iRIC) graphical user interface. Finite difference scheme with general coordinate systems is employed to conduct the numerical computations.

4 Results and discussions

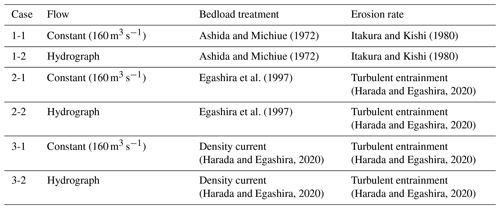
4.1 Calculation conditions

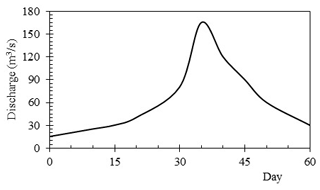
A total of 6 simulations have been conducted considering uniform sediment bed having D₅₀ of 46 µm. Two types of flow (a) constant discharge of 160 m³ s⁻¹ and (b) flow hydrograph as shown in Fig. 3 are supplied from the upstream boundary. The flow conditions are defined in order to understand the erosion-deposition process during the peak discharge as well as under the non-uniform flow condition. The computational domain is long enough. There are no time series of measured water levels at the downstream boundary. Therefore, it is assumed that the water surface at downstream boundary is parallel to the river bed surface and the flow condition in the downstream boundary is defined as uniform flow. The initial bed elevation is defined based on the measured bathymetric data. There are no measured sediment data at the upstream boundary. Therefore, the sediment boundary condition is defined by assuming an exponential distribution of suspended sediment in vertical direction and equilibrium sediment concentration profile for the conventional method. The computational domain is divided into 11 420 grids having Δx=35 m and Δy=12 m. The time step for numerical simulation is 0.5 s. The details of numerical simulations conditions are shown below in Table 1.

Figure 3 Flow hydrograph supplied at upstream boundary during numerical simulations.

4.2 Riverbed evolution and morphological changes

Figure 4 is the results showing the riverbed evolution in terms of riverbed aggradation and degradation obtained by numerical simulations using bedload formulae having functional form proportional to ${\mathit{\tau }}_{\ast }^{\mathrm{1.5}}$ (Ashida and Michiue, 1972). The erosion rate of bed sediment is evaluated by conventional method following the formula of Itakura and Kishi (1980). Figure 4a is the resultant riverbed level changes after passing a constant discharge (160 m³ s⁻¹) for 20 d, whereas Fig. 4b shows the results after passing the hydrograph as shown in Fig. 3. Figure 4a shows that riverbed degradation takes place actively along the channel centre with riverbed aggradation in bank region. Figure 4b shows riverbed degradation around the bend. However, in both cases, more than 7 m of river bed aggradation and degradation is observed.

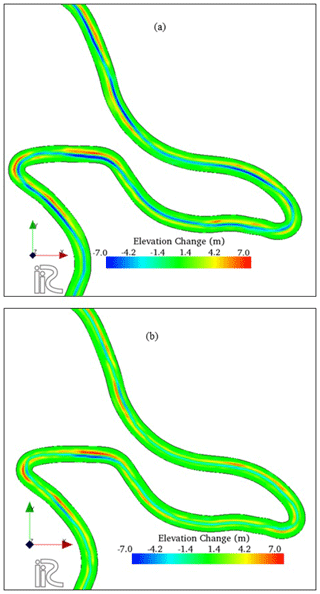
Figure 4 Riverbed evolution based on Ashida and Michiue (1972) and Itakura and Kishi (1980) formulae for (a) constant discharge, (b) for hydrograph.

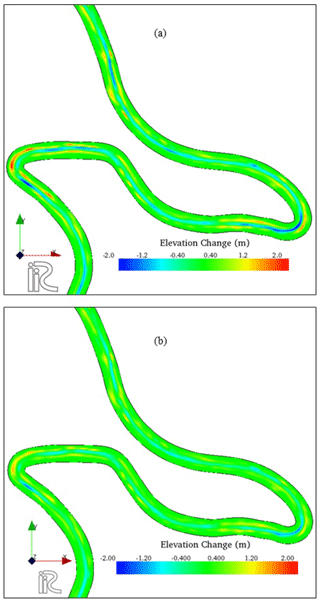
Figure 5 Riverbed evolution for constant discharge (a) visco-coulomb and (b) Egashira et al. (1997) formula with entrainment velocity concept.

Figure 5a shows the results of riverbed aggradation and degradation that are obtained from numerical simulations by employing visco-coulomb model for the bedload rate. Figure 5b is the results showing riverbed evolution by bedload a formula having functional form proportional to ${\mathit{\tau }}_{\ast }^{\mathrm{2.5}}$. In both cases, erosion rate is evaluated by applying the entrainment velocity concept. The results indicate active bed lowering around the bend. The bed degradation in conventional method is about 3 times higher comparing to the same in the entrainment velocity concept.

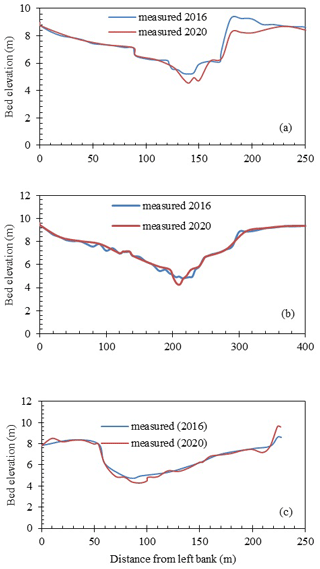
Figure 6 Changes in riverbed between 2016 and 2020 at (a) XS-5 (b) XS-6 and (c) XS-7 based on measured data.

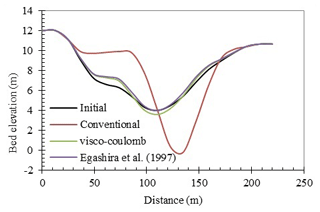
Figure 7 Comparison between river cross-sections at XS-7 based on simulated data using conventional method, visco-coulomb and Egashira et al. (1997) using a constant discharge of 160 m³ s⁻¹.

The difference instigates due to the treatment of sediment entrainment. The results suggest that the equilibrium reference sediment concentration determined by the conventional method is comparatively high. Figure 6 is the actual changes in cross-section in the field at XS-5, XS-6 and XS-7 between 2016 to 2020. XS-5 is located at the upstream and XS-7 is located at downstream. The observed data shows very small riverbed degradation at each of the cross-sections. This indicates the erosion and deposition process are almost balancing each other. Figure 7 shows simulated cross-section at XS-7 after 20 d for a constant discharge of 160 m³ s⁻¹. The results suggest active bed degradation at the channel centre for the computation with conventional method. According to Harada et al. (2022), equilibrium reference suspended sediment concentration predicted with the orthodox approaches exhibits higher sediment concentration for fine sediment particles. The erosion rate which is the product of equilibrium reference suspended sediment concentration and the particle fall velocity results comparatively higher value. The simulated results also show similar tendency which differ from the data obtained from the field observations The results obtained with the entrainment velocity concept are found to capture the bed degradation process and show better agreement with the data from field investigations.

5 Summary

Suspended sediment transportation has a remarkable non-equilibrium characteristic. The present study discusses riverbed evolution and associated morphological changes based on the results of numerical simulations and field observation in a reach of Bhairab River in Bangladesh where the riverbed is composed of very fine sediment. Results of the present study primarily support the following main conclusions:

1. Erosion rates evaluated with entrainment velocity concept and equilibrium sediment concentration produce noticeable dissimilarities in the channel planform from identical initial channel geometry, riverbed slope, sediment size distribution and roughness conditions after experiencing similar flow condition.

2. The predicted bed degradation with the conventional method is about 3 times higher comparing to the same in the entrainment velocity concept.

3. The cross-section profiles obtained from numerical simulations with entrainment velocity concept are consistent with the data from field investigations.

4. It is extremely difficult to examine the applicability of the bed-load equation to a suspended sediment dominated river. The present simulations have been conducted based on measured bathymetric and grain size distribution data only. Considering the issue of limited measured data and uncertainty of sediment transport, the results will be further verified based on the rigorous field observations.