the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Estimation bayésienne des courbes de tarage et des incertitudes associées : application de la méthode BaRatin au Congo à Brazzaville
Jérôme Le Coz
Guy D. Moukandi N'kaya
Jean-Pierre Bricquet
Alain Laraque
Benjamin Renard
L'inférence bayésienne est une approche intéressante pour estimer les courbes de tarage hauteur-débit des stations hydrométriques et les incertitudes associées car elle permet de croiser les jaugeages et la connaissance a priori des contrôles hydrauliques dans un cadre probabiliste. Utilisable par tous à travers un logiciel gratuit et simple d'utilisation, la méthode BaRatin est ici illustrée avec une application récente à l'analyse de la courbe de tarage du fleuve Congo à l'échelle de Brazzaville. Par rapport aux ajustements conventionnels de courbes de tarage, l'approche bayésienne est basée sur des hypothèses explicites sur les contrôles hydrauliques et fournit une décomposition des sources d'incertitude sur les débits. Ceci facilite la justification et la révision future de la courbe de tarage, et permet une utilisation éclairée des données hydrométriques. La série des débits avec incertitudes du Congo à Brazzaville depuis 1902 ainsi calculée présente des incertitudes très réduites.
- Article
(1026 KB) - Full-text XML
- BibTeX
- EndNote
Pour la plupart des cours d'eau disposant d'une station hydrométrique, la série temporelle de débit (ou hydrogramme) est établie en appliquant un modèle hauteur-débit (ou courbe de tarage) à la série temporelle des hauteurs d'eau (ou limnigramme) mesurée en continu à la station. La construction et l'estimation de cette courbe de tarage est un problème complexe qui nécessite de combiner des mesures (appelées jaugeages) ponctuelles et incertaines du couple hauteur-débit avec l'expertise (également incertaine) de l'hydromètre sur les contrôles hydrauliques de sa station. Ces contrôles sont les caractéristiques physiques du chenal ou de la section critique qui déterminent la hauteur d'eau au point de mesure en fonction du débit du cours d'eau. L'inférence bayésienne est une approche intéressante pour ce type de problème car elle permet de croiser les deux sources d'information incertaine dans un cadre probabiliste pour estimer la courbe de tarage et les incertitudes associées. Plusieurs méthodes basées sur le principe bayésien ont été proposées ces dernières années (Kiang et al., 2018), dont la méthode BaRatin (pour Bayesian Rating curve, Le Coz et al., 2014). A travers le logiciel gratuit BaRatinAGE en versions anglaise et française, BaRatin est maintenant utilisé par différents services hydrométriques opérationnels et différents groupes de recherche ou d'ingénierie à travers le monde. La méthode est ici illustrée avec une application récente à l'analyse de la courbe de tarage du fleuve Congo à l'échelle de Brazzaville, plus grande station hydrométrique du continent africain par son bassin versant et par son débit moyen.
2.1 Le Congo à Brazzaville-Kinshasa
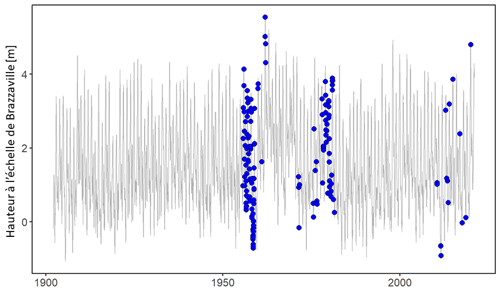
Le fleuve Congo est le deuxième de la planète et le premier du continent africain par la superficie de son bassin versant (près de 3,8 × 106 km2) et par son débit moyen interannuel (40 500 m3/s pour la période 1902–2020). Ce fleuve long de 4700 km présente dans sa partie aval un régime équatorial bimodal, avec sa crue principale en décembre et sa secondaire en mai (Alsdorf et al., 2016). C'est au niveau du bief qui sépare les capitales Brazzaville et Kinshasa sur le pourtour du Pool Malebo qu'ont débuté les mesures hydrologiques sur le fleuve Congo, avec des relevés quotidiens de hauteur d'eau depuis fin 1902 jusqu'à aujourd'hui (Devroey, 1957; Mateba 22, 1957). Environ dix kilomètres en aval, le Pool Malébo se termine avec les barres rocheuses des rapides du Djoué, au début des chutes de Livingstone. Grâce à un important travail documentaire et l'accès à la base de données SIEREM de l'IRD, les hauteurs d'eau ainsi qu'un riche ensemble de jaugeages historiques (Van Ganse, 1959; Lempicka, 1973; Molinier, 1979; Moukandi N'kaya et al., 2020) ont pu être réunis pour cette étude de la courbe de tarage du Congo à l'échelle de Brazzaville (Fig. 1). En rapportant les relevés de hauteur d'eau faits à Kinshasa à l'échelle de Brazzaville via une régression linéaire, on obtient une longue série hydrométrique sur une station couvrant près de 98 % de la superficie du bassin versant du Congo. L'amplitude des hauteurs d'eau relevées entre 1902 et 2020 va de −1 à 5,55 m. Les incertitudes de mesure (au niveau de probabilité de 95 %) des relevés de hauteur d'eau ont été supposées égales à ±5 cm après le 1er janvier 1955 (lecture directe de l'échelle de Brazzaville) et à ±10 cm avant, pour tenir compte des erreurs dues au transfert des cotes lues à l'échelle de Kinshasa vers celle de Brazzaville.
2.2 Jaugeages et incertitudes
Sur les périodes 1955–1962 et 1971–1981, 139 jaugeages au moulinet sont disponibles. Ils ont été complétés à partir de 2010 grâce à 15 autres mesurés par ADCP dans le cadre d'une coopération internationale. Ils couvrent tout le cycle hydrologique ainsi que la quasi-totalité du marnage observé sur les 120 dernières années (Fig. 1). Eu égard aux conditions de mesure très difficiles sur le Congo avec les moyens de jaugeage de l'époque, les incertitudes de mesure (au niveau de probabilité de 95 %) ont été supposées égales à ±15 % pour l'ensemble des jaugeages au moulinet sauf pour les quatre plus élevés, réalisés dans des conditions de mesure extrêmes (débits supérieurs à 70 000 m3/s), pour lesquels l'incertitude est estimée à ±20 %. L'incertitude des jaugeages par ADCP réalisés à partir de 2010 est estimée à ±10 %. La méthode de détection des détarages proposée par Darienzo et al. (2021), basée sur une segmentation des résidus jaugeages/courbe de tarage tenant compte des incertitudes, a été appliquée à l'ensemble du jeu de jaugeages. Aucun détarage n'est détecté.
2.3 Méthode BaRatin
La méthode bayésienne BaRatin (Le Coz et al., 2014) permet la construction des courbes de tarage hauteur-débit avec estimation de l'incertitude, en combinant la connaissance a priori sur les contrôles hydrauliques et le contenu d'information des jaugeages incertains. L'équation de la courbe de tarage est dérivée de la combinaison de fonctions puissance pour chacun des contrôles supposés pour le site. L'utilisateur définit également les distributions de probabilité a priori des paramètres physiques de cette équation hauteur-débit, «a priori» signifiant sans utiliser les jaugeages utilisés dans l'estimation bayésienne. Une telle estimation bayésienne est basée sur l'échantillonnage par méthode Monte Carlo par Chaîne de Markov (MCMC) de la distribution a posteriori des paramètres de la courbe de tarage, inférée à partir du théorème de Bayes. L'hydrogramme avec incertitudes est calculé à partir des réalisations de la courbe de tarage et du limnigramme avec incertitudes selon la méthode de propagation décrite par Horner et al. (2018).
3.1 Définition des a priori hydrauliques
Le modèle de courbe de tarage du Congo à Brazzaville est bâti sur l'hypothèse d'un unique contrôle par déversoir rectangulaire représentant les premiers rapides du Djoué, à l'aval immédiat du Pool Malebo. L'équation donnant le débit Q (en m3/s) en fonction de la hauteur d'eau h (en m) est donc :
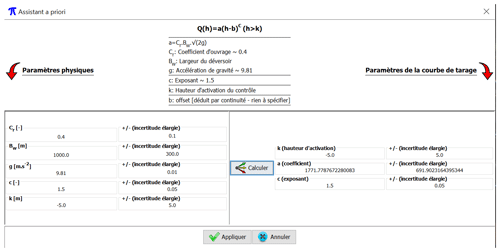
où C est le coefficient de débit du déversoir, g l'accélération de la gravité, B la largeur déversante du déversoir, h0 la cote moyenne de la crête du déversoir, et n un exposant. Les a priori sur les différents paramètres sont exprimés sous forme de distributions gaussiennes (les incertitudes indiquées ci-après correspondent à deux fois l'écart-type, soit un niveau de probabilité de 95 %). Le coefficient est estimé comme un seul paramètre du modèle. La valeur centrale et l'incertitude de ce coefficient sont calculées par propagation selon la méthode du GUM (JCGM 100, 2008). Les a priori sont les suivants : C= 0,4 ± 0,1 (valeur typique d'un déversoir rectangulaire), g= 9,81 ± 0,01 m/s2, m (estimé par vue satellite Google Earth, au resserrement le plus étroit en aval du Pool Malebo et présentant un dénivelé brusque, identifié comme la section de contrôle dite des rapides du Djoué), m (estimé grossièrement d'après les plus basses valeurs du limnigramme), et n= 1,5 ± 0,05 (exposant théorique pour un déversoir rectangulaire).
L'interface graphique du logiciel BaRatinAGE, d'utilisation simple, permet à l'opérateur de spécifier cette connaissance a priori des contrôles hydrauliques (Fig. 2). Cette information est traduite par le logiciel sous forme d'une équation de courbe de tarage et de distributions de probabilité a priori des paramètres de cette équation. Dans l'exemple présenté ici, le Congo à Brazzaville, le modèle de courbe de tarage est très simple car réduit à un seul contrôle hydraulique pour toute la gamme de hauteurs d'eau possibles. BaRatin permet aussi de modéliser une courbe de tarage en considérant un ensemble de contrôles par chenal (loi de Manning-Strickler) ou par section critique (lois de déversoir ou d'orifice) qui s'ajoutent ou se succèdent les uns aux autres sur des segments de hauteur d'eau.
3.2 Estimation de la courbe de tarage
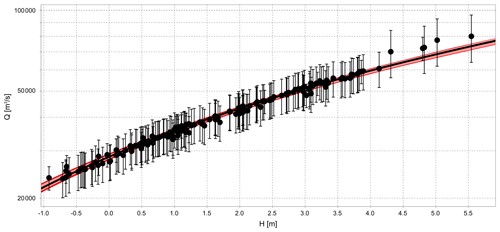
En combinant l'information a priori et la vraisemblance des observations (les jaugeages munis de leurs incertitudes), le théorème de Bayes permet de calculer (à une constante près) la distribution a posteriori des paramètres de la courbe de tarage, qui est échantillonnée par méthode Monte Carlo par Chaîne de Markov (MCMC). Les résultats sont probabilistes : les échantillons permettent de calculer l'enveloppe d'incertitude au niveau de probabilité souhaité (95 % par défaut). L'incertitude totale combine une incertitude dite paramétrique, traduisant l'incertitude d'estimation des paramètres de l'équation de la courbe de tarage, et une incertitude dite restante (ou structurelle) nécessaire à réconcilier les jaugeages et la courbe de tarage. Cette dernière composante d'incertitude peut traduire les limites du modèle de courbe de tarage pour représenter les contrôles hydrauliques réels de la station et leur éventuelle évolution dans le temps (détarages, influence aval, végétation … ). Parmi le grand nombre d'échantillons, on retient la courbe de tarage «MaxPost» calculée avec le jeu de paramètres échantillonné qui maximise la densité a posteriori. Pour le Congo à Brazzaville (Fig. 3), cette courbe de tarage «MaxPost» vaut :
Dans la gamme jaugée ainsi que pour les très basses eaux, la courbe de tarage BaRatin est très proche de la courbe de tarage historique ORSTOM établie à partir des jaugeages au moulinet sur la période 1971–1979. On constate néanmoins qu'au-dessus de h= 4,2 m et Q=70 000 m3/s, les quatre jaugeages de la crue de 1961–1962 ainsi que le jaugeage ADCP de la forte crue de décembre 2019 sont alignés environ 10 % au-dessus de la courbe de tarage BaRatin. Cette dernière reste statistiquement cohérente avec l'ensemble des jaugeages disponibles et leurs incertitudes propres. Cependant, la pertinence des hypothèses hydrauliques faites sur le contrôle (déversoir unique, sans élargissement en forte crue) jouant en partie sur le haut de la courbe méritera d'être évaluée à l'avenir, à l'aide de futurs jaugeages ADCP en crue. L'incertitude de la courbe de tarage du Congo à Brazzaville (Fig. 3) est extrêmement faible (inférieure à 3 % environ) sur la gamme jaugée (entre 30 000 et 80 000 m3/s), les parties extrapolées en hautes et basses eaux étant très réduites. L'incertitude sur les hautes eaux est toutefois peut-être sous-estimée si l'hypothèse d'un contrôle unique se révélait fausse.
3.3 Estimation de la série de débit
Selon la méthode exposée par Horner et al. (2018), chaque échantillon de courbe de tarage est croisé avec un échantillon de hauteur d'eau, issu de l'incertitude spécifiée pour le limnigramme, pour calculer un échantillon de débit. On calcule ainsi l'hydrogramme assorti de son incertitude. L'incertitude des débits calculés pour le Congo à Brazzaville entre 1902 et 2020 varie entre 2 % et 5 % avec une moyenne et une médiane de 3 %. Le budget d'incertitude, c'est-à-dire la contribution relative des sources d'incertitude à l'incertitude totale, peut différer selon les périodes considérées. Pour la forte crue de 1961–1962, l'incertitude paramétrique (plage en rose sur la Fig. 4a) domine largement les incertitudes structurelle et limnimétrique. Avant 1955, en raison du transfert des cotes de l'échelle de Kinshasa vers celle de Brazzaville, l'incertitude due aux relevés de hauteur d'eau (plage en jaune sur la Fig. 4b, exemple de l'étiage sévère de 1905) est plus importante qu'après 1955 et domine le budget d'incertitude, en particulier pour les basses eaux. Mais le contrôle par les rapides du Djoué présentant une excellente sensibilité sur toute la gamme de débit, les incertitudes dues aux relevés de hauteur d'eau n'entraînent que de faibles incertitudes sur l'hydrogramme.
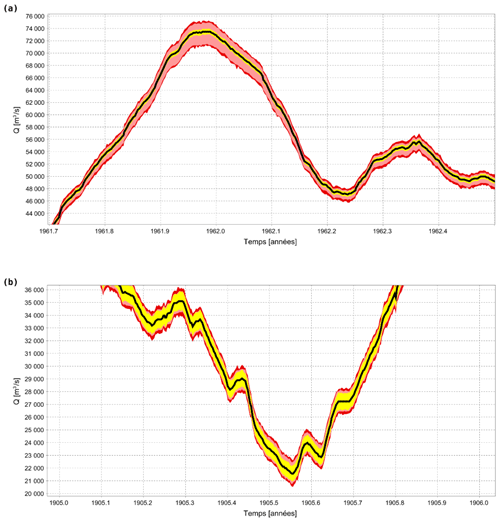
Figure 4Hydrogrammes avec incertitudes du Congo à Brazzaville calculés par BaRatin pour (a) la plus forte crue enregistrée (1961–1962) et (b) l'étiage sévère de 1905. Les enveloppes d'incertitude à 95 % correspondent à la combinaison des incertitudes du limnigramme (en jaune), et des incertitudes paramétrique (en rose) et structurelle (en rouge) de la courbe de tarage.
La méthode bayésienne BaRatin permet d'établir la courbe de tarage et l'hydrogramme munis de leurs incertitudes d'une station hydrométrique fonctionnant avec une relation hauteur-débit univoque. Par rapport aux ajustements conventionnels de courbes de tarage, l'approche bayésienne est basée sur des hypothèses explicites sur les contrôles hydrauliques et fournit une décomposition des sources d'incertitude sur les débits. Cette méthode est ici illustrée avec l'application à la station du Congo à Brazzaville. Grâce au bassin de tranquillisation constitué par le Pool Malébo et par le contrôle stable et sensible des rapides du Djoué, la courbe de tarage et la longue série de débits depuis 1902 présentent des incertitudes très réduites. De futurs jaugeages restent néanmoins nécessaires, notamment en hautes eaux pour confirmer la pertinence du modèle hydraulique par contrôle unique, et en basses eaux pour confirmer l'absence de détarage significatif.
Le logiciel BaRatinAGE est disponible sur simple demande à baratin.dev@lists.irstea.fr.
Les données sont disponibles sur demande auprès des auteurs.
JLC a effectué les calculs et rédigé le manuscrit. GDMN'k, JPB et AL ont réuni et critiqué les données, expertisé le site de mesure et relu et corrigé les résultats. BR a contribué à la méthode de calcul, et vérifié les résultats et l'article.
Les auteurs déclarent qu'ils n'ont aucun conflit d'intérêts.
Publisher’s note : Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “Hydrology of Large River Basins of Africa”. It is a result of the 4th International Conference on the ”Hydrology of the Great Rivers of Africa”, Cotonou, Benin, 13–20 November 2021.
Les producteurs historiques et actuels des données des stations hydrométriques de Kinshasa et Brazzaville sont chaleureusement remerciés.
Alsdorf, D., Beighley, D., Laraque, A., Lee, H., Tshimanga, R., O'Loughlin, F., Mahé, G., Dinga, B., Moukandi N'kaya, G., and Spencer, R. G. M. : Opportunities for hydrologic research in the Congo Basin, Rev. Geophys., 54, 378–409, https://doi.org/10.1002/2016RG000517, 2016.
Darienzo, M., Le Coz, J., Renard, B., and Lang, M. : Detection of stage-discharge rating shifts using gaugings : a recursive segmentation procedure accounting for observational and model uncertainties, Water Resour. Res., 57, e2020WR028607, https://doi.org/10.1029/2020WR028607, 2021.
Devroey, E. J. : Annuaire hydrologique du Congo belge et du Ruanda-Urundi, Académie royale des Sciences coloniales, Classe des Sciences Techniques, Mémoires in-8∘, Nouvelle série, Tome X, fasc. 1, Bruxelles, 1957.
Horner, I., Renard, B., Le Coz, J., Branger, F., McMillan, H. K., and Pierrefeu, G. : Impact of stage measurement errors on streamflow uncertainty, Water Resour. Res., 54, 1952–1976, 2018.
Joint Committee for Guides in Metrology (JCGM 100) : 2008 : Evaluation of measurement data – Guide to the expression of uncertainty in measurement (GUM), JCGM (Joint Committee for Guides in Metrology), BIPM, Sèvres, France, 2008.
Kiang, J. E., Gazoorian, C., McMillan, H., Coxon, G., Le Coz, J., Westerberg, I., Belleville, A., Sevrez, D., Sikorsk, A. E., Petersen-Øverleir, A., Reitan, T., Freer, J., Renard, B., Mansanarez, V., and Mason, R. : A comparison of methods for streamflow uncertainty estimation, Water Resour. Res., 54, 7149–7176, 2018.
Le Coz, J., Renard, B., Bonnifait, L., Branger, F., and Le Boursicaud, R. : Combining hydraulic knowledge and uncertain gaugings in the estimation of hydrometric rating curves : a Bayesian approach, J. Hydrol., 509, 573–587, 2014.
Lempicka, M. : Bilan hydrique du bassin du fleuve Zaïre. I : Ecoulement du bassin 1950–1959, Office National de la Recherche et du Développement, Kinshasa, République Démocratique du Congo, 1973.
Mateba 22 : Observations Limnimétriques : Kinshasa-Matadi-Boma, Inventaire 1903–1983 Navigabilité du bief maritime du fleuve Zaïre, Laboratoire de Recherches Hydrauliques, Borgerhout, Chatelet, Royaume de Belgique, 1984.
Molinier, M. : Note sur les débits et la qualité des eaux du Congo à Brazzaville, Cah, ORSTOM Série Hydrol., 16, 55–66, 1979.
Moukandi N'kaya, G. D., Orange, D., Bayonne Padou, S. M., Datok, P., and Laraque, A. : Temporal variability of sediments, dissolved solids and dissolved organic matter fluxes in the Congo River at Brazzaville/Kinshasa, Geosciences, 10, 341, https://doi.org/10.3390/geosciences10090341, 2020.
Van Ganse, R. : Les débits du fleuve Congo à Léopoldville et à Inga, Bull. Séanc. Acad. r. Sci. colon., Bruxelles, nouvelle série, 5, 737–763, 1959.