Changing climate and implications for water use in the Hetao Basin, Yellow River, China

Balancing water allocations in river basins between upstream irrigated agriculture and downstream cities, industry and environments is a global challenge. The effects of changing allocations are exemplified in the arid Hetao Irrigation District on the Yellow River, one of China's three largest irrigation districts. Amongst the many challenges there, the impact of changing climate on future irrigation water demand is an underlying concern. In this paper we analyse trends in local climate data from the late 1950s and consider the implications for irrigation in the Basin. Since 1958, daily minimum temperatures, T_min in the Basin have increased at three times the rate of daily maximum temperatures, T_max. Despite this, there has been no significant increases in annual precipitation, P or pan evaporation, E_pan. The difference between the increasing trends in T_max and T_min means that the average annual diurnal temperature range, DTR, has decreased very significantly, part of a global phenomenon. Hargreaves empirical approach is used to estimate changes in both incoming solar radiation, R_s, and potential evaporation, ET₀. Changes in estimated ET₀ correlated well with changes in measured pan evaporation, E_pan. Paradoxically, the estimated decreasing trend in R_s does not correspond to a significant decreasing trend in E_pan. Implications of changing climate on water use and soil salinity in the Basin are discussed.

1 Introduction

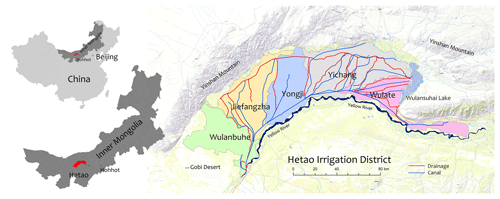
The world-wide challenge of allocating water fairly between competing upstream and downstream users and the environment is exemplified in the Yellow River, the so-called “cradle of civilization” in China (Xu et al., 2005). The challenge is compounded when upstream uses include vital irrigated food production systems. The 10 000 km² Hetao Irrigation District on the northern side of the Ordos loop of the Yellow River is one of China's three largest irrigation areas. This arid, cold region (Peel et al., 2007) in Inner Mongolia has been farmed for 2300 years, since the Qin dynasty. It is an important source of grains, oil seeds, sugar, fruits, vegetables and poultry.

Increasing water abstractions from the Yellow River for irrigation, downstream demands from rapidly expanding industrial and urban developments, obligatory environmental flows, coupled to channel elevation changes due to sediment deposition have all severely stressed the river system (Xu et al., 2005; Tang et al., 2008; Lehane, 2015). In response the Yellow River Water Conservancy Commission mandated a 15 % reduction in irrigation supply to Hetao to be phased in over time with a reduced supply target of 4.0 km³ yr⁻¹ for the Hetao District.

Figure 1 The Hetao Irrigation District Inner Mongolia, showing the five irrigation sub-districts.

Recent research in Hetao has focussed on reducing water use while maintaining or increasing productivity (e.g. IWC-IM, 1999; Xu et al., 2010; Xue and Ren, 2017). Air temperatures have increased at a significant rate in northern and western China (Tang et al., 2010) and the impacts of climate change on irrigation water demand is a continuing concern for both regulators and irrigators. In this work we analyse trends in local measured climate parameters across Hetao, relate them to physical mechanisms and consider the implications of the already observed climate changes on irrigation water demand and salinity management.

2 Materials and methods

2.1 Hetao irrigation district

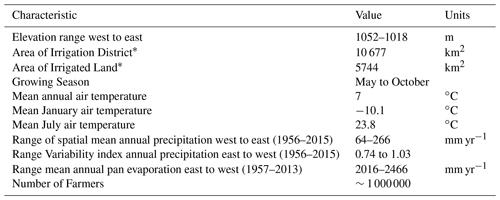
The general features of the flat, bow-shaped, approximately 200 km long by 50 km wide Hetao Irrigation District are in Fig. 1 and listed in Table 1. The District is bounded to the west by the Gobi Desert, to the north by the western portion of the Yinshan Mountains and by the Yellow River in the south. This region of northern China has experienced significant increasing trends in maximum and temperatures over the past 60 years (Fig. 2). From April until early November, water is diverted from the Yellow River at Dengkou on the southwestern edge of the region and distributed throughout the District by a series of multi-level canals. Drainage discharges into Wulansuhai Lake in the eastern edge of the region.

Table 1 Characteristics of the Hetao Irrigation District.

^* Yang (2005).

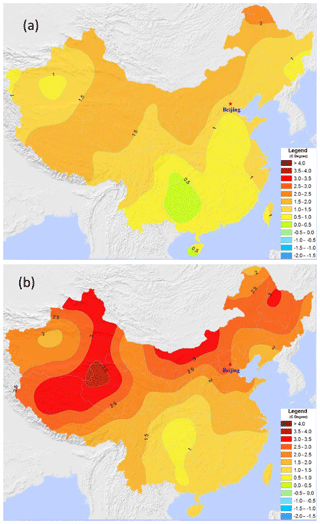
Figure 2 Trends in spatially interpolated (a) mean daily maximum and (b) minimum temperatures (^∘C/100 years) in China between 1956 and 2015.

The Basin is divided into five sub-districts: Yigan (previously called Wulanbuhe), Jiefangzha, Yongji, Yichang and Wulate comprising 19.2 %, 20.7 %, 16.2 %, 30 % and 13.9 % of the total area of the District. Annual pan evaporation, E_pan across the District, far exceeds annual precipitation and the variability of annual rainfall decreases with increasing rainfall across the District from west to east as does E_pan (Table 1).

2.2 Sources of data

This study used data drawn from a range of disparate and scattered sources collected by different organisations over diverse time periods (Table 2).

Table 2 Data sources used in this work.

2.2.1 Basin climate

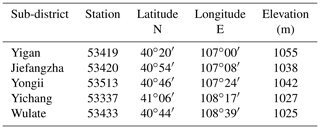
Monthly precipitation data was available from five available stations, each within one of the five irrigation sub-districts (Table 3). Monthly E_pan data was available for this study from the Yongii and Wulate stations in Table 3 for the period 1957 to 2013 together with daily maximum and minimum temperatures, T_max and T_min, from 1957 and 1954, respectively, to 2013. Mean monthly precipitation peaks in July and August. Because of this, mean pan evaporation peaks earlier in May but mean temperature peaks in July. On average mean atmospheric temperatures are at or below zero for 5 months of the year.

Table 3 The five climate stations used to assess precipitation across Hetao (west to east) for the period 1957 to 2013.

2.2.2 Temporal trends in climate data

Trends in annual temperature, DTR, precipitation, and pan evaporation, irrigation supply, specific irrigation drainage, and groundwater and drainage salinity were determined using linear regression (LR). Trends were considered not significant when the probability, p, was less than 0.9. Because of the sensitivity of linear regression trends to start and end values of a series, weaker trends (p<0.95) were also tested using the nonparametric (NP) Theil–Sen slope estimator (Theil, 1950). The significance of nonparametric trends was determined using the Mann–Kendall test (Kendall, 1970).

2.2.3 DTR and incoming solar radiation, R_s

The daily DTR (^∘C) is defined as:

$$\begin{array}{}\text{(1)}& \mathrm{DTR}=T_{\max }-T_{\min }.\end{array}$$

FAO-56 (Allen et al., 1998) pointed out that DTR can be used as an indicator of the fraction of extra-terrestrial radiation, R_a (MJ m⁻² d⁻¹), that reaches the earth's surface. Hargreaves and Samani (1982) (see also Hargreaves and Allen, 2003) proposed that the ratio of incoming solar radiation incident on the earth's surface, R_s (MJ m⁻² d⁻¹), to R_a can be approximated by the empirical relation:

$$\begin{array}{}\text{(2)}& R_{\mathrm{s}}/R_{\mathrm{a}}=k_{R_{\mathrm{s}}}{\mathrm{DTR}}^{\mathrm{1}/\mathrm{2}}\end{array}$$

where $k_{R_{\mathrm{s}}}$ (^∘C^−0.5) is an empirical adjustment coefficient (0.16 for interior regions, 0.19 for coastal regions).

Using estimates of mid-monthly R_a from FAO-56 and the latitude of the stations in Table 3, together with $k_{R_{\mathrm{s}}}=\mathrm{0.16}$ (^∘C^−0.5) in Eq. (2) and DTR data, temporal changes in the annual incoming solar radiation to Hetao can be estimated.

Good daily T_max and T_min data are available from 1958 to 2013 for two sites, Yongii and Wulate in the Hetao Basin listed in Table 3.

2.2.4 DTR and potential evaporation, ET₀

Temperature is not the main driver of ET₀. In the Penman–Monteith approach, ET₀ can be expressed as (FAO-56, Allen et al., 1998):

$$\begin{array}{}\text{(3)}& {\mathrm{ET}}_{\mathrm{0}}=C_{\mathrm{1}}\left[(\mathrm{1}-\mathit{\alpha })\cdot R_{\mathrm{S}}-R_{\mathrm{nl}}-G\right]+C_{\mathrm{2}}f(u,\mathrm{\Delta }e).\end{array}$$

In Eq. (3), C₁, C₂ are factors which depend weakly on temperature, pressure and crop characteristics, α the surface albedo, R_nl the net outgoing long wave radiation, G the soil heat flux, u the wind speed and Δe the water vapour pressure deficit. The first term in Eq. (3) represents the key contribution of R_s to ET₀, the second term represents the “drying power of the air”. For arid locations, such as Hetao, the “drying power of the air” is expected to contribute significantly to ET₀, although evaporation of surrounding irrigation water may confound this locally.

For Hetao, available long-term data necessary to fully evaluate trends in ET₀ via the Penman–Monteith approach is not readily available. FAO-56 suggest that the approach developed by Hargreaves (Hargreaves and Samani, 1982, 1985; Hargreaves, 1994), based on daily T_max and T_min give useful estimates of ET₀, particularly over periods longer than 5 d:

$$\begin{array}{}\text{(4)}& {\mathrm{ET}}_{\mathrm{0}}=\mathrm{0.0023}\cdot R_{\mathrm{a}}(\stackrel{\mathrm{‾}}{T}+\mathrm{17.8}){\mathrm{DTR}}^{\mathrm{0.5}}\end{array}$$

with $\stackrel{\mathrm{‾}}{T}=(T_{\max }-T_{\min })\mathrm{2}$.

Using Eq. (2), Eq. (4) can be written in terms of R_s as:

$$\begin{array}{}\text{(5)}& {\mathrm{ET}}_{\mathrm{0}}=\mathrm{0.0023}\cdot (\stackrel{\mathrm{‾}}{T}+\mathrm{17.8})R_{\mathrm{s}}/k_{R_{\mathrm{s}}}.\end{array}$$

FAO-56 noted that the 1985 Hargreaves' method, Eq. (4), “has shown reasonable ET₀ results with global validity”. Hargreaves and Allen (2003) did an extensive evaluation of Eq. (4) over a very wide range of global locations against the FAO-56 Penman Monteith method and concluded that: “Where equipment cost is a consideration, where data quality is questionable, or where historical data are missing, both the reduced set FAO-PM or the 1985 Hargreaves are recommended, since the two methods are surprisingly equivalent over a wide range of climates.” Use over 5 d or longer is recommended because of the influence of moving weather fronts, and large variations of wind speed and cloud cover at daily time steps.

Equation (4) appears to compensate for the lack of R_n, humidity and wind speed data required by the Penman–Monteith method. The diurnal temperature range in the equation implicitly accounts for the influence of cloudiness because DTR decreases with increasing cloudiness. As well, it has been shown that DTR correlates with relative humidity and vapor pressure deficit and is inversely influenced by wind run (Hargreaves and Allen, 2003). Hargreaves and Allen (2003) recommend that Eq. (4) should be calibrated against Penman–Monteith combination equations to produce a regionally calibrated relationship.

The temporal trend in ET₀ with time follows from Eq. (5),

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\partial {\mathrm{ET}}_{\mathrm{0}}}{\partial t}}={\displaystyle \frac{\mathrm{0.0023}}{k_{R_{\mathrm{s}}}}}\left(R_{\mathrm{s}}\cdot {\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{T}}{\partial t}}+[\stackrel{\mathrm{‾}}{T}+\mathrm{17.8}].{\displaystyle \frac{\partial R_{\mathrm{s}}}{\partial t}}\right).\end{array}$$

Whether estimated ET₀ will increase or decrease with time will depend on the relative magnitude of the two terms $R_{\mathrm{s}}\frac{\partial \stackrel{\mathrm{‾}}{T}}{\partial t}$ and $[\stackrel{\mathrm{‾}}{T}+\mathrm{17.8}]\frac{\partial R_{\mathrm{s}}}{\partial t}$ in Eq. (6) which may be of opposite sign.

3 Climate trends in the basin

3.1 Temperature

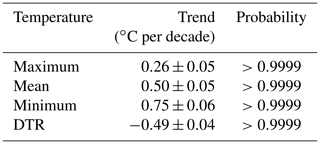
The trends in annual mean daily T_max and T_min at Yongii and Wulate over the period 1958 to 2013 were identical. As a result, the area-averaged mean temperature is used here as representative of the Hetao Basin. Figure 3 plots the average annual mean daily T_max and T_min average and annual mean daily precipitation, pan evaporation and temperature as a function of time. Table 4 shows that both increasing temperature trends were highly significant with T_min increasing almost three times the rate of T_max.

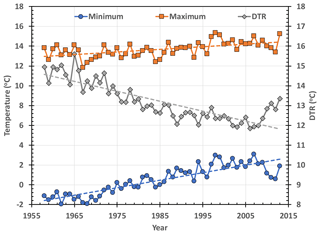
Figure 3 Increasing significant trends in the area-averaged annual mean daily maximum and minimum temperatures combined from the two stations, Yongii and Wulate in Table 3 and the decreasing significant trend in mean DTR for the period 1958 to 2013.

Table 4 Increasing trends in the average annual daily maximum, mean and minimum temperatures and DTR in Hetao for the period 1958 to 2013.

Analysis of monthly mean daily temperature data in Hetao shows that T_min in all months of the year have increased very significantly and are also increasing at a greater rate than monthly T_max. Figure 4 shows the change in the distribution of measured monthly minimum temperatures with time in Hetao as well as the projected temperature distribution for 2050 using the highly significant monthly increasing trends. Because the distribution of monthly temperatures depends on precipitation, the years chosen in Fig. 4 were selected because they had similar annual precipitations, (1960: P=155 mm; 1991: P=151 mm; 2006; P=156 mm; with the projected precipitation for 2050 of 157 mm).

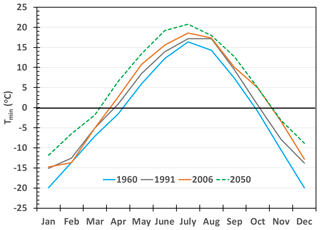
Figure 4 Change in the distribution of area-averaged monthly minimum temperatures in Hetao. Values for 1960, 1991 and 2006 are actual measured distributions from years with similar annual precipitation and that for 2050 is projected from monthly trends.

Figure 4 demonstrates that by 2006, the period over which the minimum temperature in Hetao was below zero had decreased by almost 2 months relative to that for 1960 so that the length of the growing season in Hetao is expanding due to increasing minimum temperatures. This also suggests that the depth to which the soil is frozen and the length of time it is frozen for has decreased. This may have implications for salt flushing from topsoil.

3.2 Annual precipitation and E_pan

Area-weighted average annual precipitation for the Basin between 1957 and 2013 is plotted in Fig. 5. The large variations in annual rainfall over the period 1957 to 2013, from 64 to 288 mm yr⁻¹, are apparent. The small trend, 0.3±4.3 mm per decade, however, is not significant (p<0.9).

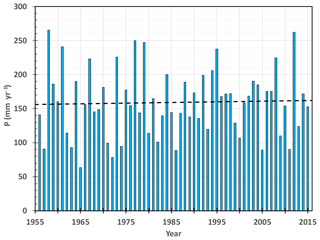
Figure 5 Areal-averaged annual precipitation of the Hetao Basin, 1957 to 2013. The linear trend is not significant.

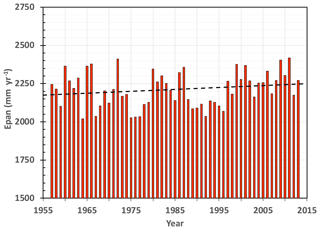
The area-averaged E_pan for Hetao, between 1957 and 2013 is plotted in Fig. 6. An increasing linear regression trend of $+\mathrm{13}\pm \mathrm{9}$ mm per decade can be seen. NP analysis gave a similar trend of +15 mm/ per decade. For both analyses, however, the trends were not significant (p<0.9). So, the highly significant increasing annual maximum and minimum temperatures in Hetao are not associated with any significant increases in annual precipitation or annual pan evaporation between 1957 and 2013.

Figure 6 Area-averaged pan evaporation for the Hetao Basin, 1957 to 2013. The linear trend is not significant.

3.3 Trends in DTR

Because T_min increased at three times the rate of T_max, DTR decreased significantly (Fig. 3) at −0.49 ^∘C per decade over the period 1958–2013. This is the same absolute rate as annual mean daily temperature is increasing (Table 4).

Analyse of the data revealed that between 1958 and 1985, DTR decreased at faster rate, $-\mathrm{0.85}\pm \mathrm{0.10}$ ^∘C per decade (p>0.9999) than the full period 1958 to 2013. Between 1985 to 2013, however, the trend $-\mathrm{0.03}\pm \mathrm{0.09}$ ^∘C per decade was not significant (p<0.9). This change in trend is consistent with regionally-averaged northern hemisphere data where DTR was found to decrease significantly from 1950 to the late 1970's. Between 1979 and 2004, however there was no significant trend in DTR (Vose et al., 2005). This appears to coincide with a fundamental shift in the El Niño–Southern Oscillation phenomenon (Easterling et al., 1997).

3.3.1 Decreasing DTR and changes in R_s

Equation (2) was used to estimate temporal changes in R_s using the DTR data using the method of Hargreaves and Samani (1982). The results are given in Fig. 7 which suggests the annual incoming solar radiation to Hetao decreased at a rate of $-\mathrm{105.6}\pm \mathrm{10.2}$ MJ m⁻² per decade (p>0.9999) between 1958 and 2014, or 9 % over 50 years. This is close to the 10 % to 20 % reduction reported in many places over the same period (Stanhill and Cohen, 2001). This global phenomenon is attributed by some to global “dimming” (a decrease in net radiation due to increased cloudiness or aerosols) (Easterling et al., 1997; Vose et al., 2005). It is noted in Fig. 7, however, that from about 2009 onwards, there appears to have been an increase in annual R_s.

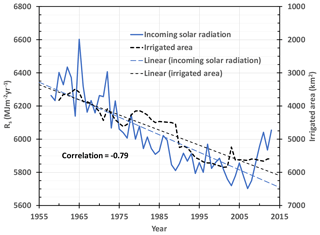
Figure 7 Estimated temporal change of incoming solar radiation to Hetao from 1958 to 2013 using Eq. (2). Also shown is the change in area of land irrigated (plotted in reverse order) and significant linear trends.

The overall decrease in estimated R_s cannot be attributed to increasing cloudiness due to increasing annual precipitation, since, as shown above, annual precipitation in Hetao has not increased significantly between 1957 and 2013. The correlation between estimated annual R_s and annual precipitation, P is weakly significant (p>0.9) with $\partial R_{\mathrm{S}}/\partial P=-\mathrm{1.0}\pm \mathrm{0.6}$ MJ m⁻² mm⁻¹. This correlation between R_s and P appears to be mainly due to a correlation with fluctuations around the decreasing trend in R_s Some of the fluctuations of R_s about the trend line in Fig. 7 may be caused by annual changes in cloud cover associated with annual variations in precipitation.

From Eq. (3) it is expected that the decrease in incoming solar radiation in Fig. 7 associated with a decrease in potential evaporation in Hetao. We next examine that proposition.

3.3.2 DTR and ET₀

In discussing Eq. (6) above it was noted that any trend in ET₀ will depend on the terms $R_{\mathrm{s}}\frac{\partial \stackrel{\mathrm{‾}}{T}}{\partial t}$ and $[\stackrel{\mathrm{‾}}{T}+\mathrm{17.8}]\frac{\partial R_{\mathrm{s}}}{\partial t}$. In Hetao, $\frac{\partial \stackrel{\mathrm{‾}}{T}}{\partial t}>\mathrm{0}$ (Table 4) but $\frac{\partial R_{\mathrm{s}}}{\partial t}<\mathrm{0}$ (Fig. 7), so depending on their relative magnitudes, ET₀ could increase, decrease or remain constant with time.

Monthly values of ET₀ were estimated from Eq. (5) which were summed to give an estimate of annual ET₀. The estimated change of ET₀ between 1958 and 2013 is plotted in Fig. 8.

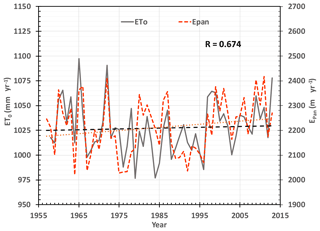
Figure 8 Comparison between annual potential evaporation estimated from Eq. (5) and the area weighted annual pan evaporation for Hetao over the period 1958 to 2013. The linear temporal trends are not significant.

The temporal trend in annual ET₀ estimated from Eq. (5), shown in Fig. 8, using linear regression, is $\partial {\mathrm{ET}}_{\mathrm{0}}/\partial t=+\mathrm{0.8}\pm \mathrm{2.2}$ mm yr⁻¹ per decade. Nonparametric analysis gave a trend of +1.7 mm yr⁻¹ per decade. Both trend estimates were not significant (p<0.9) over the period 1958 to 2013.

Over this period, the mean annual potential evaporation estimated from Eq. (5) was 1027±26. This is considerably larger than the actual evapotranspiration evaluated by Hao and Yang (2016) using two approaches based on a water balance approach and using NDVI and the FAO-56 Penman–Monteith equation. Their water balance for the period 1960 to 2013 gave actual annual evaporation of 601 mm yr⁻¹ and the NDVI Penman–Monteith approach gave 605 mm yr⁻¹ for the period 2006–2010. Yang et al. (2012) used remote sensing to estimate evapotranspiration over the cropping season and found a mean value of 605 mm yr⁻¹ between the years 2000 and 2010. Over the May to September growing season Eq. (5) predicts that ET₀ was 742±21 mm. Hargreaves and Allen (2003) recommended that Eq. (6) should be calibrated against Penman–Monteith combination equations to produce a regionally calibrated relationship.

3.3.3 Estimated ET₀ and measured E_pan

Figure 8 shows the comparison between annual ET₀ estimated from Eq. (8) and area weighted annual E_pan for Hetao. Between 1958 and 2013, the correlation between ET₀ and E_pan was very significant (p>0.99999) with correlation, R=0.67. As discussed previously, the linear regression trend in pan evaporation, $\partial E_{\mathrm{pan}}/\partial t=+\mathrm{13}\pm \mathrm{9}$ mm per decade was not significant (p<0.9) as was the trend in estimated ET₀. From 1958 to 1975 the correlation between ET₀ and E_pan was stronger, R=0.83 (p>0.9999) but between 1976 and 2013, the correlation was lower, R=0.59 but still very significant (p>0.9999).

This comparison has demonstrated a reasonably good correlation between annual ET₀estimated from Eq. (8) and area weighted mean pan evaporation, E_pan, for Hetao. It also reveals that despite the significant increasing maximum and minimum temperatures and the significant decreases in DTR and in estimated R_s, there are no significant trends in either estimated ET₀ or in E_pan over the period 1958 and 2013.

4 Discussion

The dramatic trends found in annual mean daily T_max and T_min between 1958 and 2013 in the Hetao Basin are not accompanied by any significant trends in annual precipitation or pan evaporation. The significant disparity between the rates of change T_max and T_min mean that DTR is decreasing. This is accord with world-wide observations (e.g. Stanhill and Cohen, 2001). In Hetao, however, the rate of decline of DTR seems more intense and has persisted longer than elsewhere. Decreases in DTR and in E_pan (not found here) have been variously attributed to global “dimming” (a decrease in net radiation due to increased cloudiness or aerosols) or global “stilling” (a decrease in wind speed close to the surface) (Easterling et al., 1997; Stanhill and Cohen, 2001; Roderick and Farquhar, 2002; Vose et al., 2005).

Numerous hypotheses have been advanced for the changes occurring globally in DTR and in E_pan including changes in cloud cover, aerosol concentrations, precipitation, soil moisture, atmospheric circulation, land use and decreasing wind speeds (Peterson et al., 1999; Roderick and Farquhar, 2004; Vose et al. 2005; Roderick et al., 2007; McVicar et al., 2012). The consensus is that decreasing DTR is a consequence of firstly a general decrease in net radiation, and secondly a decrease in wind speed close to the surface.

It was found here that that between 1958 and 1985, DTR decreased at faster rate than over the full period 1958 to 2013. Between 1985 to 2013, however, the was not significant. This change in trend is consistent with regionally-averaged northern hemisphere data (Vose et al. 2005). This change in trend appears to coincide with a fundamental shift in the El Niño–Southern Oscillation phenomenon (Easterling et al., 1997).

In Hetao, one explanation for the changing trend in DTR could be the impact of evaporation of surrounding irrigation water. Increase in water vapour concentration in the atmosphere decreases R_s but increases in coming long-wave radiation at night, raising T_min. If this is the case, one might expect that the area of land being irrigated might impact on estimated R_s. Figure 8 compares the decreasing trend in estimated R_s with the increasing trend in irrigated land area. There is a strong, highly significant negative correlation, $R=-\mathrm{0.79}$. The decline in trend in R_s after 1985 also corresponds approximately to a period of almost no growth in irrigated area and to the use of plastic film on the soil surface to minimise soil evaporation. While correlation does not imply causality, the impact of the extent of irrigation on incoming short wave and long-wave radiation is worth researching.

Despite the estimated decline in R_s, there was no significant trend in E_pan or estimated ET₀ between 1958 and 2013. This absence of a trend appears to imply that the declining radiative component is balanced by an increasing drying power of the air. This is counter intuitive since the 46 % increase in area irrigated in Hetao between 1960 and 2013 should have decreased the water saturation deficit. In terms of Eq. (5), the absence of a significant annual trend in ET₀ over the full period indicates $R_{\mathrm{s}}\frac{\partial \stackrel{\mathrm{‾}}{T}}{\partial t}\approx -[\stackrel{\mathrm{‾}}{T}+\mathrm{17.8}]\frac{\partial R_{\mathrm{s}}}{\partial t}$.

The annual ET₀ estimated here using the empirical approach of Hargreaves were higher than other available estimates but correlated well with measured E_pan. It has been recommended that despite widespread testing of the Hargreaves approach, its estimates of ET₀ should be calibrated locally.

Implications of changing climate

The available data in the Hetao Basin shows that between 1958 and 2013, annual mean daily minimum temperatures increased at three times the rate of maximum temperatures. Between 1960 and 2010, the period over which minimum temperatures were below zero decreased by over one month. If these increases continue, by 2050 that period could decrease by two months. That may imply a longer growing season and increased water demand in Hetao.

These increasing temperatures also mean that topsoil in the Basin will be frozen for a shorter period and to a shallower depth than in the past. Soil freezing has at least two important roles. Firstly, it appears to promote formation of soil structure and improves early season infiltration and root growth. Secondly, the propagation of the freezing front downwards may expel salt that accumulated over the growing season deeper into the soil profile and away from the root zone. A decrease in the time and depth the soil is frozen may lead to a lower efficiency of salt removal.

5 Conclusions

Annual daily temperatures in the Inner Mongolia region of northern China have increased dramatically over the past 60 years. The limited available records in Hetao show that the period that temperatures are below zero has shortened significantly suggesting that the length of the growing season is expanding. Because minimum temperatures are increasing at three times the rate of maximum temperatures, DTR is decreasing. This implies that either incoming solar radiation or wind run is decreasing or both.

Despite the dramatic change in temperatures, annual rainfall, pan evaporation and estimated potential evaporation, have no significant trends over this period. This means that only an expansion of the length of the growing season could cause an increase in future water demand.

The rapid increase in T_min means that if the trend continues, the soil will be frozen for a shorter period and to a shallower depth. This has implications for soil structure formation, infiltration and root growth as well as the efficiency of salt flushing from the soil. All require further research.