the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Creep consolidation in land subsidence modelling; integrating geotechnical and hydrological approaches in a new MODFLOW package (SUB-CR)
Henk Kooi
Gilles Erkens
Creep and secondary consolidation are important phenomena in settlement caused by surface loads, but not commonly considered in land subsidence driven by groundwater extraction. To explore the role of creep in such settings, a new MODFLOW-2005 land subsidence package was developed that incorporates a creep formulation gleaned from geotechnical software. This formulation, which is based on the isotache concept, is an extension of, and incorporates the classical elastoplastic compression model of Terzaghi as a limiting case. The package is introduced, and results are presented of an application to a site in northern Jakarta. It is shown that the isotache model requires considerably higher overconsolidation levels of clays than the Terzaghi model, and that creep contributes to subsidence long after drawdown in pumped aquifers has stabilized, a phenomenon that is traditionally attributed to “hydrodynamic lag”.
- Article
(1842 KB) - Full-text XML
- BibTeX
- EndNote
Volume loss by creep of “soft sediments” (clay, silt, peat) is a well-known and crucial part of the settlement caused by surface loads such as earth embankments or surcharge that is applied for construction of roads and residential areas in areas underlain by clay or peat. Continued slow settlement, long after pore pressures have equilibrated – this is generally referred to as secondary consolidation – is a key exponent of creep. Creep can be described as viscous compression. Having to account for creep is a no-brainer in settlement evaluation in engineering practice in deltas where soft sediments are pervasive. However, when volume loss and compaction of the same types of sediment is caused by the exploitation of groundwater resources, creep is seldom considered. This is odd and lacks a proper justification.
To be able to explore the implications of creep in aquifer system compaction and land subsidence due to groundwater exploitation, a MODFLOW-2005 land subsidence package SUB-CR was developed that incorporates an isotache-based, viscoelastic compression model that is used in certified geotechnical software for settlement modelling in The Netherlands and other countries (Kooi et al., 2018).
This manuscript introduces the SUB-CR package and discusses how SUB-CR yields slightly modified perspectives on land subsidence due to groundwater use and its modelling than the existing packages (SUB, SUB-WT) that employ Terzaghi's classical elastoplastic compression model.
2.1 Basic concepts
Many basic concepts and principles of SUB-CR were borrowed from the USGS land subsidence package SUB-WT (Leake and Galloway, 2007). These concepts include 1-dimensional compression; total or geostatic stress calculated from local overburden; overburden and total stress depend on the water table; and the concept of interbeds.
Some concepts and approaches have been modified in SUB-CR. Calculation of effective stress, for instance, is done based on cell-averaged stress and pore pressure, and soil above the water table is involved in compression. In SUB-WT, effective stress (change) is evaluated for the base of model cells and unsaturated parts of cells do not contribute to subsidence. The most prominent difference, however, concerns the compression model, which is introduced in the next paragraph.
2.2 Isotache model
The isotache model (IM) implemented in SUB-CR (Fig. 1b) can be considered a generalization or extension of Terzaghi's elastoplastic compression model (TM) (Fig. 1a). σ′, and are effective stress, initial effective stress, and preconsolidation stress, respectively.
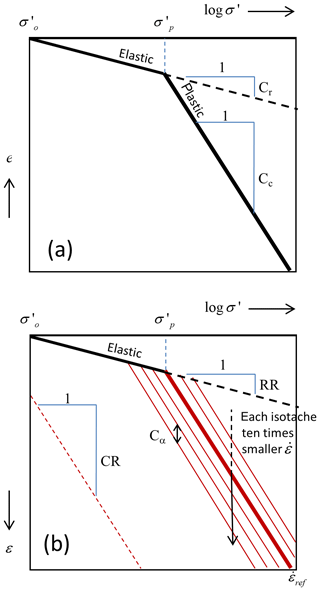
Figure 1Comparison of the stress-deformation relations in (a) Terzaghi's classical compression model (TM) and (b) the isotache model (IM).
A minor difference in the diagrams is the use of void ratio e and strain ε (positive defined here as volume decrease) along the vertical axis, which explains why Terzaghi's compression index Cc and recompression index Cr translate to compression ratio CR and recompression ratio RR in the isotache model. The key difference between the TM and the IM is that inelastic strain in the TM is (ideal) plastic, and in the IM viscous. Ideal plastic strain is instantaneous; stress directly determines strain, and each point in the diagram represents a steady state. The viscous strain in the IM implies that each combination of stress and strain is associated with a strain rate . All points at or below the elastic bounding line and its extension (dashed), therefore represent unsteady states. The viscous strain rate is referred to as creep or creep rate.
The red lines in Fig. 1b are lines of equal creep rate , or isotaches. Only a limited number of isotaches are shown for reasons of legibility. The vertical spacing (strain difference) between isotaches that differ a factor 10 in rate, is controlled by Cα, the secondary compression ratio. Mesri and Godlewski (1977) list typical values of Cα∕CR for various lithologies (e.g. 0.04±0.01 for inorganic clays and silts). The thick red line is the reference isotache (rate ) and can be regarded the equivalent of the plastic yield line in the TM. Thus, while in the TM the inelastic strain rate is infinite above the plastic yield line and zero at or below the yield line, in the IM, the reference isotache represents a nominal boundary across which the strain rate changes more gradually, controlled by Cα. Importantly, in the limit Cα→0 the isotaches are compressed on the reference isotache with infinitely high creep rates above and zero creep rates below, which is the equivalent of the TM. Thus, the TM is a limiting case of the IM. Therefore, the IM with Cα=0 is an elastoplastic model.
In the IM, is a function of the overconsolidation ratio :
where OCR=1 corresponds to the reference isotache with . Each isotache can also be represented by an intrinsic time τ through the relationship
where the reference isotache is defined as τref=1 d (derived from classical oedometer tests with time increments between load steps of 1 d). Intrinsic time can be considered an apparent age of the material (Bjerrum, 1967), where younger τ corresponds to higher creep rate and vice versa.
In SUB-CR, the IM presented here is referred to as the NEN-Bjerrum model. SUB-CR also includes another IM, called the abc-model (Den Haan, 1994), where the main difference is the use of natural (Hencky) strain εH rather than linear strain ε (Kooi et al., 2018).
2.3 Coupling with groundwater flow
For a description of the way in which SUB-CR is coupled with MODFLOW-2005, including a derivation of the underlying equations, the reader is referred to the online SUB-CR guide (Kooi et al., 2018). An important difference with the TM implemented in SUB-WT is that with the IM, creep plays an active role in enhancing pore pressure and hydraulic head by “squeezing” the sediment, a behaviour that cannot be represented by conventional specific storage coefficients and that requires an iterative solving approach.
In this section, an example application is presented that illustrates behavioural aspects of SUB-CR.
3.1 Site description and 1-dimensional approach
Illustrative results are presented for the Daan Mogot district in Jakarta (Fig. 2). The subsurface of northern Jakarta consists of mostly thin sand units of limited lateral extent, embedded in a predominantly clay-rich environment. Distinct aquifers and confining units cannot be discerned. Together with a paucity of hydraulic head and well data, this complicates development of a meaningful 3-dimensional model. Drawdown and the subsidence response are expected to be predominantly controlled by local conditions that are generally insufficiently constrained to be predicted with a reasonable degree of confidence. Daan Mogot is one of few sites in Jakarta where a geological borehole description, a GPS-based subsidence time series and head observations from a groundwater well are available in a concise area (several km2). These data have been used in a local assessment in which SUB-CR was employed in an one-dimensional column mode, and where drawdown is imposed at the depths of observation well screens to drive the subsidence.
3.2 Model runs and results
Figure 3 depicts the borehole and groundwater data and aspects of model design. With the available hydraulic head data, a scenario for drawdown development between 1925 and 2100 was constructed for the three screens of the observation well (Fig. 3c). These time series of drawdown were imposed at the modelled screen depths (Fig. 3b) using the CHD package. The water table is fixed at land surface, and the base is a no-flow boundary. The head response and consolidation of the adjacent and intermediate layers were simulated. The scenario of Fig. 3c explores how subsidence would progress for the theoretical case that hydraulic heads within the pumped layers at the well screens would be stabilized from 2025 to 2100. Other scenarios are presented by Kooi and Trysa Yuherdha (2018).
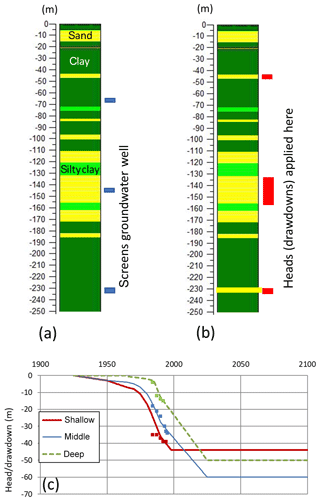
Figure 3Borehole and well-data. (a) Geological borehole description and depth of screens of the “nearby” observation well. (b) Modified borehole layering used in the modelling and depths where drawdowns are applied. (c) Observed drawdown (squares) and model time series of drawdown (lines) for the three drawdown levels.
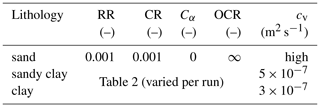
Parameter values are in part (CR, cv, ρsat) constrained by reported results of laboratory tests of various geotechnical parameters for the clayey units of the borehole. Direct information on RR, Cα and are lacking. Fixed and default parameter values in the calculations are listed in Table 1. The consolidation coefficient cv is not an input parameter of SUB-CR but was used to parameterize hydraulic conductivity k using
A value of ρsat=1700 kg m−3 was adopted for the saturated mass density of the sediments. Table 2 lists parameter values for selected model runs that provide a fair fit with the GPS-based subsidence in Daan Mogot (Fig. 4). The runs differ in terms of parameter values for the clay layers. The first four runs (Fig. 4a) include creep in the sense that Cα>0. Preconsolidation stress is set using the overconsolidation ratio . These runs will be referred to as IM-runs. The last three runs (Fig. 4b) use Cα=0 and will be referred to as TM-runs (elastoplastic). Preconsolidation stress in the TM-runs is set using the pre-overburden pressure (or overconsolidation) . This is the general approach in subsidence modelling using the existing USGS land subsidence packages such as SUB-WT.
Table 2Parameters for clay and sandy clay per run.
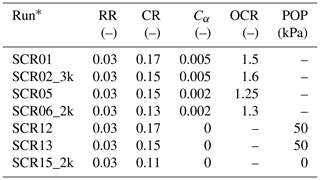
* _2k and _3k indicate that cv, and hence k is multiplied by a factor 2 and 3, respectively.
4.1 State of overconsolidation
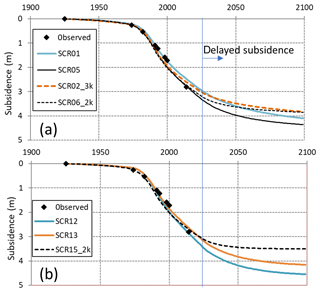
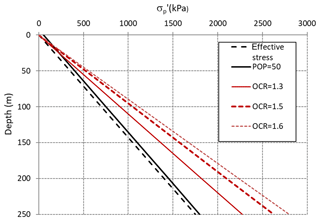
Figure 4 illustrates that the observed subsidence at Daan Mogot can be accounted for by both IM-runs (Fig. 4a) and TM-runs (Fig. 4b). The key difference is that the two types of runs require very different preconsolidation states (Fig. 5).
For TM-runs the required overconsolidation of the clayey units is very small (0–50 kPa). This applies to shallow as well as to deep levels. For larger POP values, TM-runs yield insufficient inelastic (plastic) compression and underpredict the observed subsidence. For the IM-runs, by contrast, a constant low POP describes an incompatible state, because OCR then decreases rapidly with depth to very low values, and low values of OCR correspond to very high creep rates (Eq. 1). Very high creep rates at great depth in the undisturbed situation in the year 1925 are unrealistic.
In the IM-runs a constant OCR was assumed (increasing POP with depth), which corresponds to a constant rate of creep with depth. Model results are very sensitive to OCR. Too high values yield insufficient inelastic compression and insufficient subsidence. Too low values yield too high initial creep rates and overprediction of subsidence during the earlier phase of groundwater development (1925–1970).
The main lesson to be learned is that the IM requires high overconsolidation levels (POP) for deep clay units whereas the TM suggests that overconsolidation levels are low. Quantification of the overconsolidation state of deep clays in areas that have not been impacted by large drawdown would, therefore, provide invaluable information to evaluate the IM and shed more light on the potential role of creep in land subsidence in northern Jakarta and land subsidence in general. Unfortunately, preconsolidation stress data are hardly available in Jakarta in lab-test reports. Using reported undrained shear strength data for a borehole elsewhere in Jakarta (Sunter), Kooi and Tyrsa Yuherdha (2018) inferred OCR estimates varying between 1.1 and 2.5 for clays between 25–80 m depth using an empirical relation of Mayne (2006). Although the high values cannot be readily reconciled with the TM, these estimates are considered to be insufficient to provide clear evidence for or against the IM and the role of creep.
4.2 Role in delayed subsidence
The modelled subsidence in the period 2025–2100 (Fig. 4) reflects the continued consolidation of clayey units while drawdowns in pumped sandy units are stable (Fig. 3c). In the TM-runs (Fig. 4b) the delayed subsidence is solely caused by the low permeability of the aquitards, a phenomenon known as hydrodynamic lag (e.g. Riley, 1969). In SCR15_2k, the hydraulic conductivity is double that of the other two TM-runs. This results in more efficient drainage of the aquitards and less (0.39 m) delayed subsidence (0.98 and 1.09 m for the other runs). In the IM-runs, the delayed consolidation is more complex and reflects the interplay between hydrodynamic lag (low-permeability effect) and creep. Even if hydrodynamic lag would be absent, creep would cause delayed subsidence in the form of secondary consolidation. The role of creep is most apparent in run SCR02_3k in which hydraulic conductivity is thrice the default value with still 0.81 m of delayed subsidence. Further research is required to clarify to what extent this extended delay due to creep is truly present in the natural system.
The SUB-CR package is currently being evaluated by a third party. The source code of the package is planned to be made public in the course of 2020 by Deltares, but may be provided earlier on reasonable request to the authors.
HK conceptualized the analysis, conducted the experiments and wrote the original draft of the manuscript. GE reviewed and edited the draft manuscript.
The authors declare they have no conflict of interest. Co-author Gilles Erkens is member of the editorial board of the special issue but was not responsible for the acceptance of the manuscript for publication.
This article is part of the special issue “TISOLS: the Tenth International Symposium On Land Subsidence – living with subsidence”. It is a result of the Tenth International Symposium on Land Subsidence, Delft, the Netherlands, 17–21 May 2021.
We want to thank Heri Andreas of Bandung Institute of Technology (ITB), Bandung, Indonesia, for providing the subsidence reconstruction data for the study site.
Bjerrum, L.: Engineering geology of Norwegian normally consolidated marine clays as related to settlements of buildings, Géotechn., 17, 81–118, 1967.
Den Haan, E. J.: Vertical Compression of Soils, PhD, Dissertation, Technical University of Delft, 96 pp., 1994.
Kooi, H. and Trysa Yuherdha, A.: Updated subsidence scenarios Jakarta; MODFLOW SUB-CR calculations for Sunter, Daan Mogot and Marunda, Deltares internal report 11202275_008, available at: https://www.deltares.nl/en/publication/new-subsidence-prognoses-jakarta/ (last access: 25 February 2020), 2018.
Kooi, H., Bakr, M., de Lange, G., den Haan, E., and Erkens, G.: User guide to SUB-CR; a MODFLOW package for land subsidence and aquifer system compaction that includes creep, Deltares internal report 11202275-008, available at: http://publications.deltares.nl/11202275_008.pdf (last access: 25 February 2020), 2018.
Leake, S. A. and Galloway, D. L.: MODFLOW ground-water model: user guide to the Subsidence and Aquifer-System Compaction Package (SUB-WT) for water-table aquifers, USGS Tech. and Methods Rep. 6–A23, U.S. Geological Survey, Reston, Virginia, 2007.
Mayne, P. W.: In-situ test calibrations for evaluating soil parameters, in: Chacterization and engineering properties of natural soils, edited by: Tan, T. S., Phoon, K. K., Hight, D. W., and Leroueil, S., Vol. 3, CRS Press, Boca Raton, Florida, 2006.
Mesri, G. and Godlewski, P. M.: Time- and stress- compressibility interrelationship, J. Geotech. Eng.-ASCE, 103, 417–430, 1977.
Riley, F. S.: Developments in borehole extensometry, in: Land subsidence, edited by: Johnson, A. I., IAHS Pub., 151, 169–186, 1969.