Parameterisation of the Koppejan settlement prediction model using cone penetration testing and gradient boosting

This study examines how cone penetration test (CPT) parameters, such as cone tip resistance and friction sleeve resistance, can be used to assess the compressibility of fine-grained soils across the Netherlands based on a database of 286 paired CPTs and oedometer tests from across the country. This is done with the aim of refining and simplifying the parameterisation of the Koppejan consolidation coefficients, a procedure which can yield significant error and is prone to misinterpretation. It was found that there is significant potential in using gradient boosting methods to obtain a relationship between the CPT parameters and the Koppejan parameters, with further investigation required into the noise within the dataset and the acquisition of additional high-quality samples. The use of such methods will offer a means of reducing the influence of human error or misinterpretation on the prediction of settlement and provide further confidence in the use of machine learning methods in engineering practice.

1 Introduction

Appropriately assessing the consolidation of soil under applied loads has long been a challenge for geotechnical engineers. In the case of the Netherlands, soft clays and organic soils dominate the subsurface and the heterogeneity and high compressibility of these materials has resulted in a significant margin of error being associated with settlement calculations, in the range of ±30 % for Dutch practice (CROW, 2004). This is exacerbated by the effect of human subjectivity on the parameterisation of variables associated with settlement prediction models, a process which is highly dependent on the experience and interpretation of the engineer. Furthermore, given the sporadic and random nature of soil sampling and the sample disturbance that may also result, there is also a need to correlate these variables to continuous, in situ tests in order to obtain a more representative parameter for a soil layer. The cone penetration test (CPT) is an example of such a test and involves penetrating the ground with an instrumented steel cone and rod, measuring the cone tip resistance q_c and friction sleeve resistance f_s as it penetrates through the ground. It is used almost ubiquitously throughout the Netherlands and many other countries worldwide due to the many correlations its parameters have with basic soil properties along with its ability to delineate soil stratigraphy to a high resolution.

Of the settlement prediction models in the Netherlands, the Koppejan model (Koppejan, 1948) is the most prevalent, largely due to its simplicity and cost effectiveness in comparison to the more advanced models such as the a, b, c isotache model (Den Haan, 1992, 1994) or the NEN-Bjerrum model (Bjerrum, 1967). The model has also been extensively implemented in Dutch geotechnical practice and thus, many Dutch engineers have a high competence with the model. The model is based on a combination of the logarithmic compression law proposed by Terzaghi (1925) and the creep law proposed by Buisman (1936). The Koppejan parameters can be obtained directly from incremental loading oedometer tests, a procedure which assesses the one-dimensional consolidation of a small soil specimen through the application of increasing vertical loads over time on top of the specimen.

Hence, this study aims to explore the relationship between the CPT and the Koppejan compressibility parameters using both simple linear regression and machine learning, based on a database of fine-grained clay soils obtained from sites across the Netherlands.

Figure 1 Borehole–CPT pairings across the Netherlands (©OpenStreetMap contributors YEAR. Distributed under a Creative Commons BY-SA License, see https://www.openstreetmap.org/copyright, last access: 29 August 2019).

2 Data source

2.1 Geology of the Netherlands

The Netherlands is situated in a delta formed by the Rhine, Maas and Schelde rivers with much of the country being flat and altered anthropogenically, evident from its canalised streams, polders and dikes protecting the coastline and inland regions. Most of the country is dominated by Quartenary deposits, with the western half of the country immediately underlain by a very soft Holocene layer and the east by a firm sandy Pleistocene layer (Maljers et al., 2015). In the context of engineering applications, the western Holocene layer is particularly troublesome due to its high compressibility, with structures generally requiring long piles extending down towards the Pleistocene layer below (Houkes, 2016).

2.2 Data description

The data originates primarily from road and rail projects executed by Fugro throughout the Netherlands between 2008 and 2018 (see Fig. 1). For each location, sampling boreholes were automatically paired with CPT locations less than 25 m away, with the closest CPT location chosen where applicable. Given the size of the dataset, an individual geological assessment of each site was deemed infeasible and hence, a Python algorithm was developed for the oedometer–CPT test pairing process (Duffy, 2019).

In total, 286 oedometer–CPT pairs were used for the analysis, with the Koppejan's general constant of compressibility at stresses greater than the preconsolidation pressure C, the CPT cone resistance q_c and the friction sleeve resistance f_s brought forward for further analysis.

3 Linear regression analysis

A direct visual relationship between C and the CPT parameters was not evident, with simple linear and multiple linear regression models affirming the lack of correlation, an example of which is shown in Fig. 2.

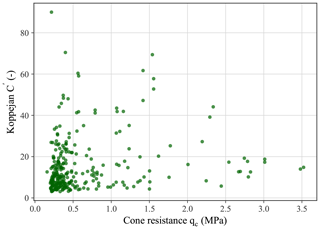
Figure 2 Plot of the Koppejan C^′ values against the corresponding cone resistance q_c, indicating the lack of a distinct visual relationship.

Based on the correlation devised by Buisman and Huizinga (1944) shown in Eq. (1), an assessment was made of the relationship between C^′, q_c and the in situ vertical effective stress parameter σ₀^′ which describes the vertical stress transmitted between soil particles at a certain depth as a result of the weight of soil above that same depth. In obtaining σ₀^′, the saturated unit weight correlation for Dutch soils derived by Lengkeek et al. (2018) was used, assuming a water table of one metre throughout.

$$\begin{array}{}\text{(1)}& C{}^{\prime }={\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{m}}{q}_{\mathrm{c}}}{{\mathit{\sigma }}_{\mathrm{0}}{}^{\prime }}},\end{array}$$

where α_m is the constrained modulus cone factor.

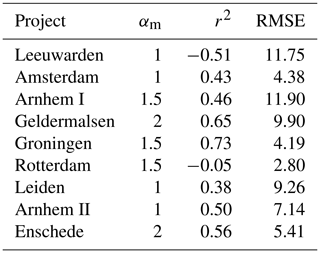
The results of this localised assessment are shown in Table 1. Results of this study have been quantified using both the root mean square error (RMSE) and the coefficient of determination (r²), a coefficient which expresses the proportion of variance explained by the statistical model and is given in its generalised form in Eq. (2):

$$\begin{array}{}\text{(2)}& r^{\mathrm{2}}=\mathrm{1}-{\displaystyle \frac{{\mathrm{SS}}_{\mathrm{res}}}{{\mathrm{SS}}_{\mathrm{tot}}}}\end{array}$$

where SS_res is the sum of squares of the residuals and SS_tot is the total sum of squares.

Indeed, although r² is the square of the correlation coefficient r in the case of simple linear regression, it may also be negative in other statistical models, indicating that the mean of the data provides a better fit to the outcome than the fitted statistical model itself.

For the most part, the correlation performs relatively well. The choice of an α_m coefficient can also be supported by look-up tables such as that by Mitchell and Gardner (1975) which uses the soil plasticity, water content and primary description. However, in the case of a single engineering project where CPT and laboratory data is significantly more limited, obtaining a robust α_m value may prove to be relatively challenging. Hence it would be optimal if a more universal correlation for the Netherlands could be found.

Table 1 Results of the project by project analysis.

4 Machine learning

In order to explore more complex non-linear patterns in the dataset, machine learning methods have been explored, including artificial neural networks, gradient boosting and XGBoost. A preliminary assessment found that gradient boosting produced the strongest results (Duffy, 2019).

4.1 Decision trees and gradient boosting

At an elementary level, decision trees are akin to a flow chart in that each “node” represents a variable, each “branch” represents a decision and each “leaf” represents an outcome. It can be used effectively for classification and regression purposes, with an example of a simple decision tree shown in Fig. 3.

In the process of creating a decision tree, the algorithm partitions the dataset into subsets of variables of similar magnitudes, ascertaining the effectiveness of potential splits as it moves through the tree. In other words, the tree assesses the improvement in model score (or reduction in error) caused by creating the split. The algorithm converges when it can no longer gain further information through the creation of more splits or when it reaches a pre-specified limit imposed on the model, known as the model's “hyperparameters”. An example of a hyperparameter may include the number of levels in the tree or the minimum number of samples required in a leaf node.

Figure 3 Example of a basic decision tree.

Boosting methods are an extension of the basic decision tree algorithm whereby the algorithm uses a combination of trees, with each new tree learning from the mistakes of previous trees. In this way, the model constantly aims to remove or reduce any pattern that may be preeminent in the residuals or the error. This is a core principle of the gradient boosting algorithm (Friedman, 2001).

4.2 Input parameters

In order to produce a result that is reliable and not a product of overfitting, 80 % of the data was randomly designated as training data, with the remaining 20 % being designated as unseen testing data. This split was chosen in order to retain a sufficient amount of testing data so a more robust and reliable result could be produced.

The input parameters chosen were q_c, the ratio between f_s and q_c (also known as the friction ratio R_f) and σ₀^′, with R_f chosen in lieu of f_s so that the possibility of any interpretability issues associated with the collinearity between q_c and f_s was avoided. C^′ was used as the output parameter.

The gradient boosting model used as part of this study was implemented using the MLPRegressor class of the scikit-learn toolbox version 0.20.3 (Pedregosa et al., 2011), with 5-fold cross-validation used for hyperparameter tuning.

4.3 Results

The model produced an r² score of 0.73 and 0.37 for the training and testing sets respectively, with 5-fold cross validation returning a mean score of 0.36 with standard deviation of 0.115. In the context of geotechnical engineering, this can be described as a “medium to strong correlation” as per the guidelines set out by Jakobsen (2014).

This model also returned feature importances of 0.34, 0.13 and 0.53 for q_c, R_f and σ₀^′ respectively. These scores highlight the role each variable plays in the calculation of the C^′, with q_c and σ₀^′ being the more dominant features in determining the model output, perhaps largely due to the relative inaccuracy associated with friction sleeve measurements (Lunne et al., 1997).

Figure 4 Learning curves for the gradient boosting model.

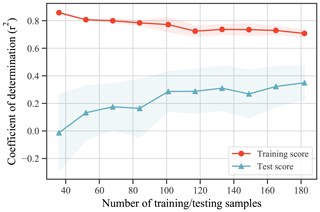
Notwithstanding, Fig. 4 shows that both the training and testing curves fail to converge together at higher sample sizes. This is indicative of variance within the model, a problem that may be resolved by increasing the number of samples and thus allowing the learning curves to converge more closely, redolent of a well-fitted model.

Figure 5 Histogram of results for the random state analysis.

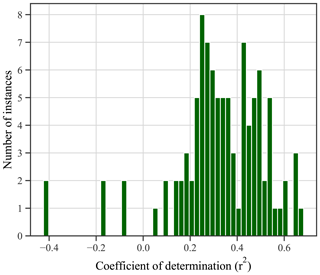
Furthermore, as illustrated by Fig. 5, there is significant fluctuation in the r² score as the random state of the model is changed. In other words, if different training and testing sets are taken and if the model learns slightly differently compared to its last execution, the model score changes significantly. Based on a collective assessment of one hundred different random states, the median and maximum r² scores obtained were 0.33 and 0.68 respectively. It is surmised that this instability is indicative of the variability and noise within the dataset, consequently leading to the presence of many local minima as the algorithms undergo gradient descent along the objective function. As a result of this, the model may be particularly prone to converging within these local minima, resulting in the dispersion of results as the random state is changed.

Consequently, it is recommended that further high-quality samples are sourced for the continued development of such an algorithm in order to yield a more complete convergence of the learning curves and to investigate the effect of the change of random state on the r² score. Further development is also required into the automated process of pairing the CPTs to the oedometer tests, with a manual assessment taken where appropriate.

5 Conclusions

A major challenge in the geotechnical engineering industry is reducing the significant amount of error associated with settlement calculations. This research has aimed to minimise the error associated with settlement prediction models by refining the parameterisation process and reducing their subjectivity by implementing a gradient boosting model, returning the appropriate Koppejan parameter based on an input of solely CPT data.

The model produced has indicated that there is some promise in using such a method in developing a universal correlation for fine-grained soils in the Netherlands and is readily extendible to other settlement prediction models upon the provision of appropriate data. However, it is apparent that further high-quality samples are required in order to produce a more robust and stable model.

Nonetheless, the results show that machine learning methods offer a means of discovering patterns in data which simpler regression methods are unable to discover and with the refinement of the CPT data, more accurate models can be developed.