the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Evapotranspiration and evaporation/transpiration partitioning with dual source energy balance models in agricultural lands
Emilie Delogu
Sameh Saadi
Wafa Chebbi
Albert Olioso
Bernard Mougenot
Pascal Fanise
Zohra Lili-Chabaane
Jean-Pierre Lagouarde
EvapoTranspiration (ET) is an important component of the water cycle, especially in semi-arid lands. Its quantification is crucial for a sustainable management of scarce water resources. A way to quantify ET is to exploit the available surface temperature data from remote sensing as a signature of the surface energy balance, including the latent heat flux. Remotely sensed energy balance models enable to estimate stress levels and, in turn, the water status of most continental surfaces. The evaporation and transpiration components of ET are also just as important in agricultural water management and ecosystem health monitoring. Single temperatures can be used with dual source energy balance models but rely on specific assumptions on raw levels of plant water stress to get both components out of a single source of information. Additional information from remote sensing data are thus required, either something specifically related to evaporation (such as surface water content) or transpiration (such as PRI or fluorescence). This works evaluates the SPARSE dual source energy balance model ability to compute not only total ET, but also water stress and transpiration/evaporation components. First, the theoretical limits of the ET component retrieval are assessed through a simulation experiment using both retrieval and prescribed modes of SPARSE with the sole surface temperature. A similar work is performed with an additional constraint, the topsoil surface soil moisture level, showing the significant improvement on the retrieval. Then, a flux dataset acquired over rainfed wheat is used to check the robustness of both stress levels and ET retrievals. In particular, retrieval of the evaporation and transpiration components is assessed in both conditions (forcing by the sole temperature or the combination of temperature and soil moisture). In our example, there is no significant difference in the performance of the total ET retrieval, since the evaporation rate retrieved from the sole surface temperature is already fairly close to the one we can reconstruct from observed surface soil moisture time series, but current work is underway to test it over other plots.
- Article
(962 KB) - Full-text XML
- BibTeX
- EndNote
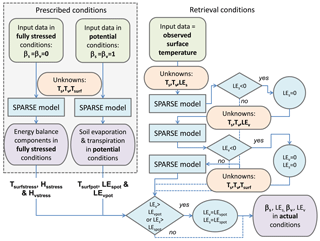
Figure 1Flowchart of the SPARSE model (T is the element skin temperature, Tsurf is the surface radiative temperature, LE is the latent heat flux and H the sensible heat flux, subscript “s” for soil and “v” for vegetation are used to characterize the component fluxes, subscripts “stress” for stressed and “pot” for potential are used to describe the water status; β is the efficiency, i.e. the ratio between actual and potential latent heat fluxes; from Saadi et al. (2018).
There is an increasing need for spatially distributed estimates of agricultural water needs and therefore evapotranspiration (ET). Estimating evapotranspiration, and, in turn, water stress, is important for irrigation monitoring and drought assessment. To do so, Remote Sensing provides an important array of data and solutions. Three spectral domains are concerned: solar (Visible/Near InfraRed spectrum, e.g. NDVI), thermal (Thermal InfraRed, e.g. surface temperature) and microwave (Radar data mostly). NDVI quantifies the amount of green vegetation, the largest water user in most areas since plants assess a larger fraction of the soil water through roots than what contributes to evaporation. Surface temperature is related to water stress through the energy budget, and gives a clue about the difference between actual and potential ET rates. Finally, radar is related to surface soil moisture and thus evaporation. While NDVI and radar, on the one hand, and NDVI and surface temperature, on the other, are frequently used together to estimate ET, the three sources of information have rarely been combined together.
ET is interesting for water management, drought assessment and irrigation control (esp. for drip or complementary irrigation), but one must also estimate separately evaporation and transpiration (the later represents the plant water uptake and the ecoagrosystem health). An estimate of the separate contribution of E and T to ET can be deduced from dual-source energy balance models such as TSEB (Kustas et al., 1999) or SPARSE (Boulet et al., 2015), but retrieving two unknowns (E and T) out of a single source of information (surface temperature Tsurf) means that an additional assumption is laid down. In TSEB or SPARSE, the initial guess on the plant water status is that, in most cases, there is no stress, and Tsurf is used to estimate E while T is computed by solving the plant energy budget in potential (i.e. unstressed) conditions. If the vegetation is suffering from water stress, its temperature will be higher than what is deduced from the energy budget in potential conditions. Consequently, the soil temperature that corresponds to the observed surface temperature and the underestimated vegetation temperature will be overestimated, and at some point this leads to a negative E retrieval. In that case TSEB and SPARSE assume that, if the vegetation is suffering from stress, the soil surface is already long dry, and E is close to zero. Tsurf is thus used to retrieve T. But how robust is this? Can we improve the robustness by forcing E and T by two RS data, Tsurf and a relative soil moisture level deduced from radar data (Schmugge et al., 1980)? This is the purpose of the present paper. It is organized in 3 main sections: the first summarize the retrieval and prescribed algorithms of SPARSE. The second is a numerical experiment assessing the limits of E and T retrievals in many configurations when using the sole surface temperature. The third section presents how forcing by both Tsurf and a relative soil moisture level affects the retrieval processes for a real case study.
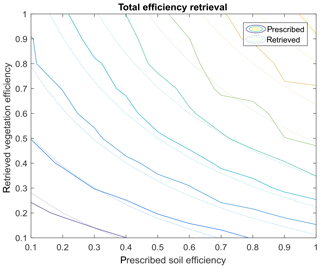
SPARSE solves the dual-source energy budget of the soil and the vegetation. The model can be run in two modes: a retrieval mode to simulate evaporation and transpiration from TIR data, and a prescribed mode which simulates evaporation and transpiration rates for known stress levels (from fully stressed, i.e. to fully potential). This enables to simulate not only actual fluxes but also surface and plant water stress. The prescribed (or direct) mode simulates fluxes and component (soil and vegetation) temperatures from known water stress conditions corresponding from any level between unstressed (potential rate) to fully stressed (minimum ET). The retrieval (or inverse) mode infer E and T from surface temperature observations using a decision tree (Fig. 1). In what follows, we use the complementary part to one of the stress, also named “efficiency”, to characterize the relative stress levels: soil evaporation efficiency βs is the ratio between the actual and potential soil evaporation rates, transpiration efficiency βv is the ratio between the actual and potential transpiration rates and the total efficiency β is the ratio between the actual and potential total evapotranspiration rates. Here, we focus on instantaneous latent heat fluxes in W m−2 at the satellite overpass time instead of daily E and T values.
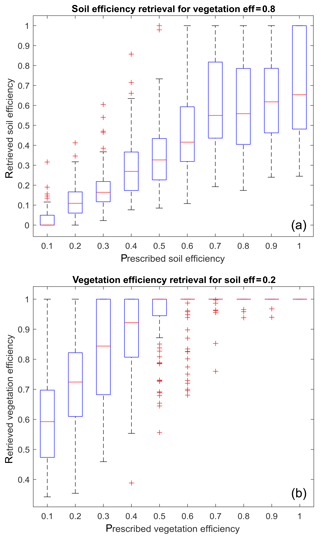
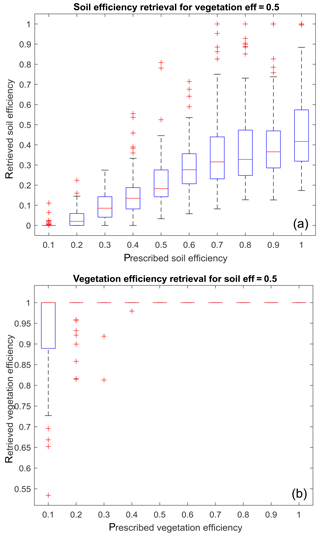
Figure 3Retrieval statistics for conditions close to the model's assumption: βs retrieval for βv=0.8 (a) and βv retrieval for βs=0.2 (b).
3.1 “Classical” configuration: using the sole surface temperature data as input for flux retrieval
In order to infer the limits of the E∕T retrieval, a synthetic study was carried out. In Fig. 1, the model is run for the two limiting cases (fully stressed, i.e. , or fully potential, ). The model in prescribed mode can also be run for any combination of relative stress levels for the soil (0 < βs < 1) and the vegetation (0 < βv < 1) and produce the corresponding component fluxes and equilibrium surface temperature. To carry out the synthetic experiment, a synthetic Tsurf was simulated using the prescribed mode for each combination of βs and βv between 0 and 1 and various climate (meteorological forcing) and vegetation cover (LAI) configurations. Each Tsurf value was then forced as input after adding a random perturbation (white noise of 1 ∘C standard deviation) for the retrieval mode. Prescribed and retrieved stress levels were then compared: ideally, if the model is perfect, prescribed and retrieved efficiencies should match. Two situations were particularly looked at: one close to the model assumption (slight vegetation stress and low surface soil mositure) and one away from it (high vegetation stress and wet soil surface, such as after a small rain event). Results for a typical dry Mediterranean midday climate in spring (global solar radiation of 900 W m−2, wind speed of 2 m s−1, relative humidity of 40 %, and air temperature of 25 ∘C) and a LAI value close to 1.2 are illustrated on Figs. 2 to 4.
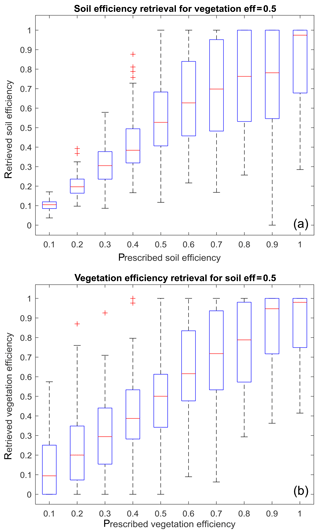
Figure 5Same as Fig. 4 when both the surface temperature and the surface soil moisture are used as inputs instead of the sole surface temperature.
Figure 2 shows the total stress isolines for each combination of evaporation and transpiration efficiencies. Figure 3 shows the retrieved efficiencies when the conditions are close to initial assumptions used by the model either for the soil (dry soil with a prescribed efficiency of 0.2) or the vegetation is transpiring at a level close to the potential rate (transpiration efficiency of 0.8). Figure 3 describes the retrieval of the soil efficiency when a fixed value of the transpiration of 0.8 is used (Fig. 3a) or the retrieved transpiration efficiencies when a fixed value of the soil evaporation efficiency of 0.2 is used (Fig. 3b), respectively. Figure 4 does the same for conditions away from the initial guess, that is a more pronounced vegetation stress (transpiration efficiency of 0.5, Fig. 4a) or a relatively wet soil (evaporation efficiency of 0.5, Fig. 4b). If total ET is always consistent between each prescribed and retrieved stress level combinations (Fig. 2), with prescribed and retrieved curve levels overlapping, it is not the case for the individual components. For instance, there is always a mismatch between retrieved (less stressed) and prescribed plant water stress levels, because the model always assumes as a first guess an unstressed canopy. This is true for the conditions close to the assumption (Fig. 3b) and even more pronounced for the conditions away from the assumption (Fig. 4b). Soil evaporation (and the associated relative efficiency) is less affected by this mismatch (Figs. 3a and 4a) and the retrieved soil evaporation efficiency follows the trend of the prescribed one, except maybe for the highest efficiency levels (retrieved efficiency reaches a plateau at around 0.6 if the prescribed transpiration efficiency is 0.8, and 0.4 if the transpiration efficiency is equal to 0.5).
3.2 Adding an additional constraint with respect to the soil evaporation efficiency
In order to improve the retrieval away from the initial assumptions, one decided to add another constraint to the retrieval process, the surface soil moisture, as it could be retrieved from remote sensing (i.e. Sentinel1 data).
Instead of using the initial guess of a fully transpiring canopy, we carry out the same experiment as in Sect. 3.1, but now evaporation is fixed by using a fixed value of the soil evaporation efficiency (as it could be derived from remote sensing). In order to account for the uncertainty related to the retrieval of soil moisture from radar data, a white noise with a 0.2 standard deviation is added to the efficiency. This value is taken from the order of magnitude of the total efficiency uncertainty from Boulet et al. (2015) at local scale and Saadi et al. (2018) for the irrigated perimeter scale. Results are presented in the Fig. 5 for conditions similar to Fig. 4 (conditions away from the model's original assumption), and show a large improvement for the vegetation efficiency retrieval (Fig. 4b).
In order to check the added value of surface soil moisture estimates to better characterize E, T and ET with real data, we did the same work for a rainfed wheat dataset (Boulet et al., 2015). The period of investigation spans an entire growing season (from emergence to harvest) and maximum LAI is around 2. ET is measured using an Eddy Covariance tower, while soil moisture at several depths is estimated from Thetaprobe soil moisture probes. An estimate of E (or its latent heat flux equivalent LEs) is derived from the observed volumetric surface soil moisture is derived from Merlin et al. (2011):
where θ0–5 cm and θsat are the topsoil (0–5 cm) measured and the saturation soil moisture respectively.
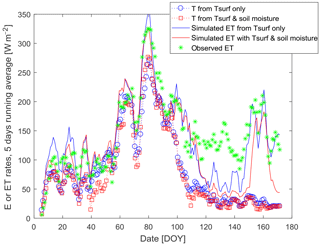
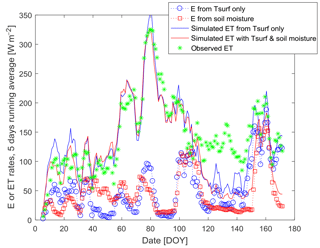
Figure 7ET by both methods, observed ET, transpiration retrieved from the sole surface temperature or from combined surface temperature/soil moisture information.
Figures 6 and 7 show the retrieved evaporation and transpiration time series together with the total simulated observed ET. In order to smooth out some of the day-to-day fluctuations of ET due to varying incoming radiation, we present in the figures a moving average over five days of the daily fluxes. Midseason simulated ET is very close to the observations, and during that time E and T simulated using the sole temperature information or adding the soil moisture constraint are very similar. At the beginning (low LAI values) or the end (senescent vegetation) of the season the model reacts to the rainfall occurrence, but with an amplitude that is either too large (overestimation, such as for DOY 5–40) or too small (large underestimation at the end of the season, DOY 110–140). For the former period, there is certainly a signifiant uncertainty in LEspot since both methods lead to similar results. For the latter period, the drop in green LAI induces a large decrease in transpiration, whereas some parts of the standing wheat are still transpiring.
The interesting result is that in fact the dual forcing does not improve the results (on the contrary, RMSE on LE at midday increases slightly from 57 to 67 W m−2). When the sole surface temperature is used as input, the evaporation at the end of the season increases in order to decrease the surface temperature, which is not possible when soil moisture is imposed. It seems that when the model performs well, i.e. around maximum growth, both versions (with or without information on surface soil moisture) perform similarly, while the poorer performances of the model for early growth or during senescence (when the green LAI drops to zero while there is obviously some transpiration from the dry standing parts) explain the difficulty to take advantage of the additional constraint in that particular case, contrarily to the result shown in the synthetic experiment. There is therefore a need for further research to balance accurately the constraint of soil moisture and surface temperature for ensuring an increased robustness in ET estimates when adding additional information.
For the data, one should contact the lead author. SPARSE model code available at http://tully.ups-tlse.fr/gilles.boulet/sparse (last access: 23 October 2018).
The authors declare that they have no conflict of interest.
This article is part of the special issue “Earth Observation for Integrated Water and Basin Management: New possibilities and challenges for adaptation to a changing environment”. It is a result of The Remote Sensing & Hydrology Symposium, Cordoba, Spain, 8–10 May 2018.
Funding from the CNES/TOSCA program for the PITEAS project is gratefully
acknowledged. We also thank the International Joint Laboratory NAILA.
Edited by: William Kustas
Reviewed by: Juan Manuel Sánchez and three anonymous referees
Boulet, G., Mougenot, B., Lhomme, J.-P., Fanise, P., Lili-Chabaane, Z., Olioso, A., Bahir, M., Rivalland, V., Jarlan, L., Merlin, O., Coudert, B., Er-Raki, S., and Lagouarde, J.-P.: The SPARSE model for the prediction of water stress and evapotranspiration components from thermal infra-red data and its evaluation over irrigated and rainfed wheat, Hydrol. Earth Syst. Sci., 19, 4653–4672, https://doi.org/10.5194/hess-19-4653-2015, 2015.
Kustas, W. P. and Norman, J. M.: Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover, Agr. Forest Meteorol., 94, 13–29, https://doi.org/10.1016/s0168-1923(99)00005-2, 1999.
Merlin, O., Al Bitar, A., Rivalland, V., Beziat, P., Ceschia, E., and Dedieu, G.: An Analytical Model of Evaporation Efficiency for Unsaturated Soil Surfaces with an Arbitrary Thickness, J. Appl. Meteorol. Climatol., 50, 457–471, https://doi.org/10.1175/2010jamc2418.1, 2011.
Saadi, S., Boulet, G., Bahir, M., Brut, A., Delogu, É., Fanise, P., Mougenot, B., Simonneaux, V., and Lili Chabaane, Z.: Assessment of actual evapotranspiration over a semiarid heterogeneous land surface by means of coupled low-resolution remote sensing data with an energy balance model: comparison to extra-large aperture scintillometer measurements, Hydrol. Earth Syst. Sci., 22, 2187–2209, https://doi.org/10.5194/hess-22-2187-2018, 2018.
Schmugge, T. J.: Effect of texture on microwave emission from soils, IEEE T. Geosci. Remote, 18, 353–361, 1980.