Parameter and input data uncertainty estimation for the assessment of water resources in two sub-basins of the Limpopo River Basin

The demand for water resources is rapidly growing, placing more strain on access to water and its management. In order to appropriately manage water resources, there is a need to accurately quantify available water resources. Unfortunately, the data required for such assessment are frequently far from sufficient in terms of availability and quality, especially in southern Africa. In this study, the uncertainty related to the estimation of water resources of two sub-basins of the Limpopo River Basin – the Mogalakwena in South Africa and the Shashe shared between Botswana and Zimbabwe – is assessed. Input data (and model parameters) are significant sources of uncertainty that should be quantified. In southern Africa water use data are among the most unreliable sources of model input data because available databases generally consist of only licensed information and actual use is generally unknown. The study assesses how these uncertainties impact the estimation of surface water resources of the sub-basins. Data on farm reservoirs and irrigated areas from various sources were collected and used to run the model. Many farm dams and large irrigation areas are located in the upper parts of the Mogalakwena sub-basin. Results indicate that water use uncertainty is small. Nevertheless, the medium to low flows are clearly impacted. The simulated mean monthly flows at the outlet of the Mogalakwena sub-basin were between 22.62 and 24.68 Mm³ per month when incorporating only the uncertainty related to the main physical runoff generating parameters. The range of total predictive uncertainty of the model increased to between 22.15 and 24.99 Mm³ when water use data such as small farm and large reservoirs and irrigation were included. For the Shashe sub-basin incorporating only uncertainty related to the main runoff parameters resulted in mean monthly flows between 11.66 and 14.54 Mm³. The range of predictive uncertainty changed to between 11.66 and 17.72 Mm³ after the uncertainty in water use information was added.

1 Introduction

The continued socio-economic development of riparian countries of the Limpopo River leads to pressure on the water resources of the basin. The management of the water resources is, therefore, critical to avoid conflict and ensure equity and accessibility to the resource for both urban and rural populations. There are also various other competing water users such as the environment (environmental water requirements), livestock farming, irrigation, and mining operations. An identification of runoff generating processes, water use and a clear understanding of their linkages within the basin are needed for improved quantification of the water resources of the basin, a requisite for better resource management. There are several challenges within the Limpopo, including shortages of water (e.g. droughts in the southern part of Zimbabwe and western Botswana), flooding (especially in the Mozambique part of the basin) and water quality issues (e.g. in the Oliphant's sub-basin in South Africa). One way of contributing to finding solutions for some of these problems is the understanding of the process linkages for improved resource quantification. However, in the absence of historical observed data (large parts of the basin are virtually ungauged) of the different aspects of the hydrology of the basin (such as rainfall, streamflow, water use, etc.) hydrological models are generally used to generate data and information that inform management and policy decision making.

Ideally, any hydrological model should be based on a sound conceptual understanding of the processes operating in the basin and should be backed by quantitative information that can be used for the parameterization of the model (Hughes et al., 2006, 2010). However, these data are often inadequate in many sub-basins, necessitating the incorporation of the uncertainty related to the estimation process. Given the diversity of the four riparian countries on data collection and management, the quantity and quality of the data in the basin varies and therefore a framework that incorporates estimates of uncertainty should be applied to deal with this challenge. Earlier studies (e.g. Matji and Görgens, 2001) have generally concentrated on the main stem of the basin and this study explains the possible uncertainty related to the modelling process.

2 Study Area

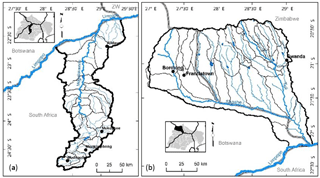
Two physically and socio-economically contrasting sub-basins were chosen for the study (Fig. 1). The Mogalakwena River rises as the Nyl River south of Mokopane flows northwards into the Limpopo (Busari, 2008). The Mogalakwena sub-basin, with a drainage area of 19 400 km², is located in South Africa and is very densely populated and industrialized incorporating the towns of Modimolle, Mookgopong, and Mokopane (Fig. 1a). The Shashe sub-basin (Fig. 1b), shared between Botswana and Zimbabwe, rises on the border of the two countries. It flows south, past Francistown (in Botswana) where after the flow changes to a south-easterly direction along the border for about 362 km until it flows into the Limpopo River.

While the sub-basins are near one another, they however have different physical characteristics such as rainfall, evaporation, soils, geology and land cover which, in turn, influence the runoff rates, water use, and abstractions. Also, since the catchments are located in different countries, the data collection methods vary affecting the data quality and availability. In South Africa, hydrological data can be accessed freely from sources such as the Water Resources Studies (1990, 2005 and 2012), national departments such as the Department of Water and Sanitation (DWS) and the Department of Agriculture, Forestry and Fisheries (DAFF), whereas hydrological data for Botswana and Zimbabwe are more difficult to access, the records of poorer quality often with missing values, and large areas are ungauged. The two study areas are therefore chosen to show the impacts of different physical and hydro-climatic data conditions on estimated water resources.

3 Data and Methodology

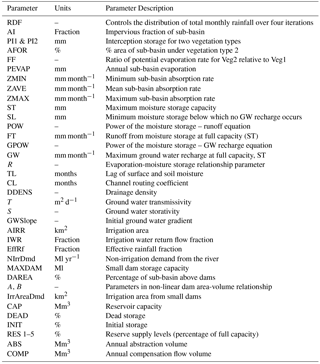
The Pitman model has been widely used for water resources assessment in most of the southern Africa region since its development in the early 1970s (Wilk and Hughes, 2002). The Spatial and Time Series Information Modelling (SPATSIM, Hughes and Forsyth, 2006) version of the Pitman model (Pitman, 1973) was used to quantify water resources of the selected sub-basins. It is a conceptual type model with parameters that are associated with components that represent the main hydrological processes (and human impacts) that operate at a sub-basin scale (Hughes et al., 2010). The SPATSIM version of the model is designed to handle multiple model runs that are required to consider uncertainty issues arising from the quantity and quality of the input data (Kapangaziwiri et al., 2012). This version also has explicit surface-ground water interaction routines (Hughes, 2004) and a wetland function. Table 1 shows the main parameters of the model (Hughes et al., 2006).

Runoff is mainly generated by two model functions. The first is an asymmetrical triangular distribution of catchment absorption rates defined by parameters ZMIN, ZAVE and ZMAX. The second function determines the drainage rate from the main moisture storage (S, with a capacity of ST, mm). This storage is depleted by evapotranspiration, interflow and groundwater recharge. The maximum interflow (FT, mm month⁻¹) and recharge (GW, mm month⁻¹) rates occur at ST, while two power functions (parameters POW and GPOW) determine these rates at lower values of moisture storage (S, mm). Recharge is routed through a groundwater storage function that accounts for evapotranspiration losses, drainage to other catchments and contributions to base flow.

Table 1 A list of the parameters of the Pitman model including those of the reservoir water balance model (Hughes et al., 2006).

The model also has functions that simulate the impact of human activities like small farm dams, large reservoirs and irrigated agriculture in managed basins. Detailed descriptions of the model can be found in Hughes et al. (2006) and Kapangaziwiri et al. (2012).

3.1 Data collection

For this study, the impact of uncertainty related to farm dam and irrigation data was evaluated. The data sources that were used include: the 2012 national water resources assessment study of South Africa (called the WR2012) database, data from the South African Department of Agriculture, Forestry and Fisheries (DAFF) and remote sensing products for the Mogalakwena sub-basin. For Shashe, besides remotely-sensed information, the data from the Limpopo River Basin Monograph study (LIMCOM, 2013) were used.

The farm dam data (and all the other data used in this study) were collected at the scale at which water resources decisions are made (i.e. at the so-called quaternary catchment for the Mogalakwena and at the sub-zone scale for Shashe). In this study, both quaternary and sub-zones are referred to just as catchment. For purposes of simplicity and also based on the model used, the individual small farm dams in each catchment were added up to form one dam at the outlet, whose parameters (e.g. full supply capacity and area) were then subsequently specified and the level of uncertainty where necessary. Only the surface areas of the identified farm dams were estimated from the remote sensing and through a manual digitizing process. The dam capacities had to be calculated using a generalised relationship between capacity and area at full supply level provided by LIMCOM (2013). While many approaches to the estimation of dam capacities could be used (e.g. Sayl et al., 2016; Hughes and Mantel, 2010 and Sawunyama et al., 2006) this equation was chosen since it was applied successfully in the whole of the Limpopo basin, and is given as:

$$\begin{array}{}\text{(1)}& \text{Surface Area}=\mathrm{0.4}\cdot {\text{(Capacity)}}^{\mathrm{0.7}}\end{array}$$

The calculated volumes were similar to those contain in existing national databases and were therefore assumed adequate to use. For running the uncertainty in the SPATSIM version of the Pitman model, minimum (Min) and maximum (Max) values are required in the model setup. The percentage differences between the average of minimum and maximum of dam volumes or irrigation areas was thus determined to represent the uncertainty. This is given by: [maximum average − minimum average)/maximum average value] × 100 (Sawunyama et al., 2011).

WR2012 irrigation data for Mogalakwena sub-basin were compared to the data received from the South African Department of Agriculture, Forestry and Fisheries (DAFF) and remotely-sensed data. For the Shashe sub-basin, the LIMCOM (2013) data were also compared to areas digitised in Google Earth.

3.2 Uncertainty analysis

The analysis focused on the impact of uncertainties related to the main physical parameters of the runoff generation process and water use data (i.e. irrigation and farm dams) on the estimation of sub-basin water resources. Parameter uncertainties were considered first, before the incorporation of water use uncertainties.

In this study, the parameter values for each run of the model are independently randomly sampled from the inputs by making use of a Normal (defined by the mean and standard deviation) frequency distribution. As soon as a parameter set generates a simulation that satisfies all of the constraints, it is saved to the SPATSIM database (Ndzabandzaba and Hughes, 2017). However, when 1000 output behavioural parameter sets have been found the model terminates. Since the constraints define the uncertainty in the hydrological response behaviour of each of the selected sub-basins (Yadav, et al., 2007; Westerberg et al., 2011, 2014) all of the saved parameter sets represents behavioural responses (Beven, 2012).

4 Results and Discussion

4.1 Uncertainty results

A significant difference between the irrigation coverage is observed for the Mogalakwena catchments giving relatively huge uncertainty. However, the difference between the irrigated areas sourced from the LIMCOM (2013) compared to the areas digitised from Google Earth is marginal, resulting in small uncertainty. Nevertheless, the uncertainty still had an impact on the low flows of the sub-basins. Shashe catchments BS4 and BS5 have little irrigated areas and the difference between the irrigated areas provided by LIMCOM (2013) and manual digitizing was too small to impact the results.

The overall calculated uncertainty of the Mogalakwena sub-basin varied between 30 and 100 % and between 5 and 100 % for the farm dams and irrigation data respectively. For the Shashe sub-basin, where farm dams and irrigation existed, the calculated uncertainty varied between 5 and 90 % and between 10 and 100 % farm dams and irrigation respectively.

4.2 Water resources simulation of the Mogalakwena sub-basin

Based solely on the uncertainty related to model parameters, the simulated monthly flows ranged between a minimum of 21.53 Mm³ and a maximum of 24.68 Mm³; resulting in a mean monthly flow of 22.62 Mm³. Results indicate that the whole range of flows (i.e. high, medium and low flows) is impacted when uncertainty related to natural parameters is considered. Adding the uncertainty related to water use (i.e. irrigation and farm dams) data resulted in minimum simulated flows of 22.15 Mm³ and a maximum of 24.99 Mm³. High flows are more impacted than low flows.

4.3 Water resources simulation for the Shashe sub-basin

The difference between the model parameters and water use uncertainties is barely noticeable for some catchments of the Shashe. This is because the cumulative volumes of the farm dams was too small to have a noticeable impact on the total predictive uncertainty. The same applies to the irrigation water use uncertainty. Considering uncertainty related to the natural parameters of runoff generation, the simulated mean monthly flow was 14.54 Mm³ with a maximum of 17.15 Mm³ and a minimum of 11.66 Mm³. When the uncertainty related to the water use data was added the minimum value of the simulated flow remained the same, whereas the maximum increased to 17.72 Mm³.

5 Conclusions

The main objective of the study was to demonstrate that estimated water resources are capable of spanning a wide range of plausible or probable values when considering the uncertainties in model parameter estimation, our understanding of the hydrological processes prevalent in a basin and how those processes are represented in the model as well as the use of limited and often poor quality historical observed data to calibrate the model. This study gives insight into how the simulation of the natural water resources of the Mogalakwena and Shashe sub-basins would be expected to vary when expected uncertainty is incorporated into the estimation process. It can be concluded that uncertainty (in this case related to parameter and water use data) plays an important role in the estimation of water resources as demonstrated in the sub-basins. The uncertainty related to the estimation of water use data tends to affect the medium to low flows more than just considering parameter uncertainty. Farm dams absorb the flows during the high flow season, whereas irrigation would be important during the low flow season. This study provides a limited illustration of how the identification and quantification of parameter and water use uncertainties can provide insight into the possible impacts of using a database such as the national water resources assessment study (WR2012) without examining the quality of the data. This study is a step forward in providing insight into water resources estimations based on the data that are routinely used in the assessment processes without examining the possible impact of the uncertainties related to those data.