Return periods in current and future climate
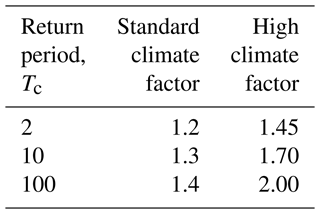
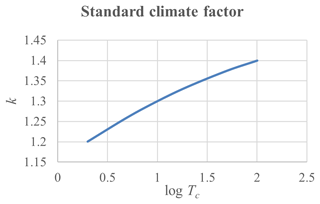
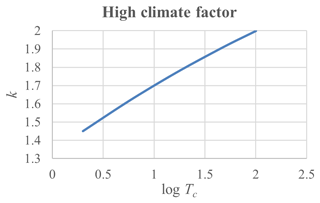
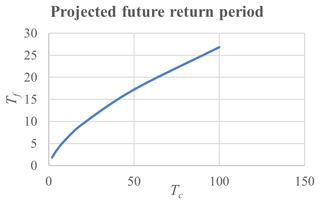
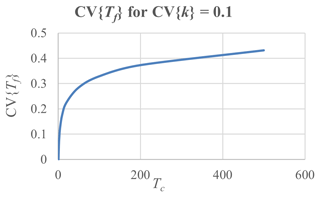
For Danish conditions, discrete rain intensity climate factors for a 100-year time horizon are generalized to continuous curves as functions of the return period. Assuming the tails of the distribution functions for T-year events to be approximately exponential, a general formula for projecting current return periods into future return periods is developed. Moreover, the uncertainty of the future T-values due to uncertainty in the climate factor is approximately assessed using first order analysis.