Geomorphometry-based modelling of discharge series in ungauged basins – Robustness regarding DEM sources

The sensitivity of a geomorphology-based hydrological modelling is evaluated according to four DEMs from 5 to 50 m resolution in Brittany, France. A set of 8 basins (5–565.7 km²) is used in a pseudo-ungauged context to explore the potential of Prediction in Ungauged Basin (PUB). The results show that despite slight differences on the stream networks extracted from DEMs and associated transfer functions, a coarse-worldwide DEM such as SRTM (25 m) supported similar performances than the finer French DEM (5 m) based on three validation indices. Finer DEMs may be useful only on headwater basins to gain a marginal performance.

1 Introduction

Prediction in Ungauged Basin remains an ambitious task, especially when dealing with discharge time series, i.e. hydrographs, and derived statistics of regimes (Blöschl et al., 2013; Hrachowitz et al., 2013). Since the beginning of DEM availability, geomorphology-based (or geomorphometry-based) approaches have proposed parsimonious, robust and flexible models with few calibration needs (Cudennec, 2007; Cudennec and de Lavenne, 2015; Rigon et al., 2015). The new availability of quasi-worldwide DEMs open new avenues for applications to simulate hydrographs with short time steps at ungauged sites, which can then be used to explore regime statistics. Cudennec (2000) proposed the inversion of a geomorphology-based transfer function to assess the space averaged net rainfall series (defined as the basin-average water signal produced by hillslopes to the river network) from a measured discharge series. The simulated discharge series at the outlet of a similar target basin is then obtained by transposition from the donor basin, i.e. generalisation of the net rainfall series, then the convolution with the corresponding transfer function. The latter is available for the target basin, thanks to the geomorphometric observation of its relief and stream network, and a robust assumption on the water velocity. This approach has been tested in three different well described contexts: semi-arid Tunisia (Boudhraâ et al., 2006, 2009, 2018), temperate oceanic France (de Lavenne et al., 2015, 2016), and pluvio-nival Québec (Ecrepont et al., 2019). A comparison of the approach with Top-Kriging (Skøien et al., 2006) has been performed and showed results of similar quality (de Lavenne et al., 2016). The robustness of the method to configuration calibration has been demonstrated on several occasions (Boudhraâ et al., 2018; de Lavenne et al., 2016), and simulations in truly ungauged basins have been performed beyond the pseudo-ungauged test configurations (de Lavenne and Cudennec, 2014, 2019; Dallery et al., 2020). But the sensitivity of the transfer function to the quality and resolution of the input DEM remains to be assessed in order to apply to less-described basins and regions, as it is often the case in the FRIEND approaches. In this study, a set of 8 basins is used to compare geomorphology-based transposition at a 15 min time step, with four DEMs spanning from coarser to accurate resolutions, including the quasi-worldwide SRTM one.

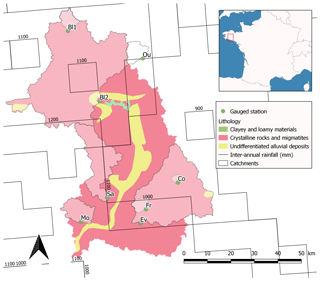
Figure 1 Geology and interannual rainfall (estimated on SAFRAN spatial grid – Habets et al., 2008) and location of the 8 basins.

Table 1 Geomorphological characteristics of the 8 basins (DEM ALTI25).

2 Material and methods

2.1 Study area

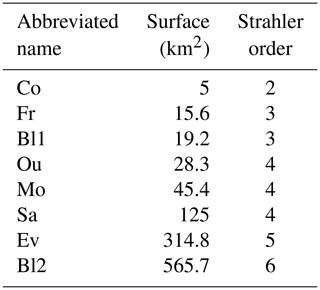
The study is performed in the central Brittany peninsula (France), in the Blavet and Oust river basins, around the Coët Dan basin at Kervidy, of the long-term hydrological observatory AgrHys (named Co in Table 1; https://www6.inra.fr/ore_agrhys_eng/, last access: 6 July 2020, Fovet et al., 2018; as in de Lavenne et al., 2015). This area of the Palaeozoic Armorican mountain range rises up to 385 m and is dominated by schist and sandstone, while the south relates to hard rocks such as granite and gneiss. The location under prevailing wind from the Atlantic Ocean on the West induces a high rainfall climatology with a mean interannual precipitation up to 1200 mm. An overview of the geology, interannual isohyets, and location of the 8 basins is available in Fig. 1. It also displays the geographic neighbouring and partly nesting configuration of the 8 basins used for the systematic pseudo-ungauged transposition analysis, while Table 1 details their sizes.

Table 2 DEMs resolution and provider.

2.2 Data

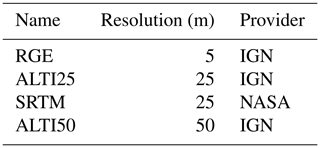
Observed runoff discharge series were extracted from the French national database “banque HYDRO” (http://www.hydro.eaufrance.fr/, last access: 6 July 2020), from January 2012 to December 2016. Four different DEMs with increasing resolution are used, three from the French IGN national agency covering France, and the SRTM one from the US NASA federal agency displaying a quasi-worldwide coverage (Table 2).

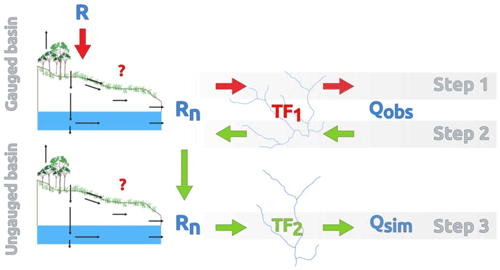
Figure 2 Deconvolution of the observed discharge series Q_obs of the donor gauged basin through the inversion of its geomorphology-based transfer function TF₁, generalization of net rainfall to a similar target basin, and simulation of the discharge series Q_sim at the outlet of the target (pseudo)-ungauged basin through the convolution with its transfer function TF₂ (from de Lavenne et al., 2015).

2.3 Methods

Simulated discharge Q is the convolution of net rainfall R_n (water flux equivalent to a height, flowing out of hillslopes to the river network), and a transfer function TF, rescaled by the basin surface S (Eq. 1).

$$\begin{array}{}\text{(1)}& \mathit{Q}=S\mathit{T}\mathit{F}\ast {\mathit{R}}_{\text{n}}\end{array}$$

For each basin and DEM, the river network was extracted with a minimum drainage threshold of 0.25 km²; then the corresponding probability density function of hydraulic length L, pdf(L), was assessed, based on a morphometric analysis with GRASS 7.4.0 (Aouissi et al., 2013). Considering a water drop falling inside a basin and moving towards the outlet, the hydraulic length L corresponds to the travelling distance within the river network. Following the assumption of a linear transfer function (Blöschl and Sivapalan, 1995; Robinson et al., 1995; Cudennec, 2007), pdf(t) = TF is then deduced from pdf(L) thanks to the estimation of the average river flow velocity v. This characteristic velocity has been regionalized for the whole Brittany by de Lavenne (2014) as in Eq. (2), where $\stackrel{\mathrm{‾}}{L}$ is the mean hydraulic length of the considered basin.

$$\begin{array}{}\text{(2)}& v=\mathrm{8.5947}\times {\mathrm{10}}^{-\mathrm{4}}\times {\stackrel{\mathrm{‾}}{L}}^{\mathrm{0.6146}}\end{array}$$

According to the theory of inverse problem (Tarantola and Valette, 1982), R_n can be estimated by the inversion of Eq. (1) (Boudhraâ et al., 2006; Cudennec, 2000). A solution of this inversion is approached by maximum likelihood on a priori net rainfall ${\mathit{R}}_{\text{n}}^{\text{ap}}$ (Boudhraâ et al., 2018) thanks to Eq. (3).

$$\begin{array}{}\text{(3)}& {\mathit{R}}_{\text{n}}={\mathit{R}}_{\text{n}}^{\text{ap}}+{\mathbf{C}}_R\mathit{T}{\mathit{F}}^t(\mathit{T}{\mathit{F}}^t{\mathbf{C}}_R\mathit{T}\mathit{F}+{\mathbf{C}}_Q{)}^{-\mathrm{1}}{\mathit{Q}}_{\text{m}}-\mathit{T}\mathit{F}{R}_{\text{n}}^{\text{ap}}\end{array}$$

where C_R and C_Q are the matrices of covariance for vectors R_n and Q, and t the transposed matrix. Contrary to Q, R_n is independent from scale and can be transferred in another (eventually ungauged) basin, then convoluted into the discharge series in the target basin, according to its own TF (Fig. 2).

The evaluation of the transposition in pseudo-ungauged basins is performed through 3 criteria given by Eqs. (4), (5) and (6); the classical “NSE” (Nash and Sutcliffe, 1970), the NSE on square rooted discharge “NSE_sqrt” (Oudin et al., 2006; Seiller et al., 2017) and the volumetric efficiency VE (Criss and Winston, 2008).

$$\begin{array}{}\text{(4)}& \text{NSE}=\mathrm{1}-{\displaystyle \frac{\sum {\left({\mathit{Q}}_{\text{obs},i}-{\mathit{Q}}_{\text{sim},i}\right)}^{\mathrm{2}}}{\sum {\left({\mathit{Q}}_{\text{obs},i}-{\stackrel{\mathrm{‾}}{\mathit{Q}}}_{\text{obs}}\right)}^{\mathrm{2}}}}\end{array}$$

$$\begin{array}{}\text{(5)}& {\text{NSE}}_{\text{sqrt}}=\mathrm{1}-{\displaystyle \frac{\sum {\left(\sqrt{{\mathit{Q}}_{\text{obs},i}}-\sqrt{{\mathit{Q}}_{\text{sim},i}}\right)}^{\mathrm{2}}}{\sum {\left(\sqrt{{\mathit{Q}}_{\text{obs},i}}-{\stackrel{\mathrm{‾}}{\sqrt{\mathit{Q}}}}_{\text{obs}}\right)}^{\mathrm{2}}}}\end{array}$$

$$\begin{array}{}\text{(6)}& \text{VE}=\mathrm{1}-{\displaystyle \frac{\sum \left|{\mathit{Q}}_{\text{obs}}-{\mathit{Q}}_{\text{sim}}\right|}{\sum {\mathit{Q}}_{\text{obs}}}}\end{array}$$

3 Results

3.1 Stream network

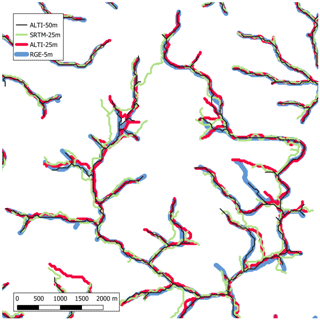
Structural differences of stream networks extracted from the different DEMs are illustrated on Fig. 3. The shapes of the networks are similar between DEMs, but some differences may appear, especially in headwaters. ALTI25, ALTI50 and RGE give similar stream networks despite their strongly different resolutions. The stream network extracted from SRTM is in the same range of differences.

Figure 3 Comparison of the stream network extraction for all DEMs on a random zone of Bl2.

Figure 4 Simulation performance for 3 criteria and 4 DEMs, for all basins, and from all donor basins.

3.2 Performance in simulation

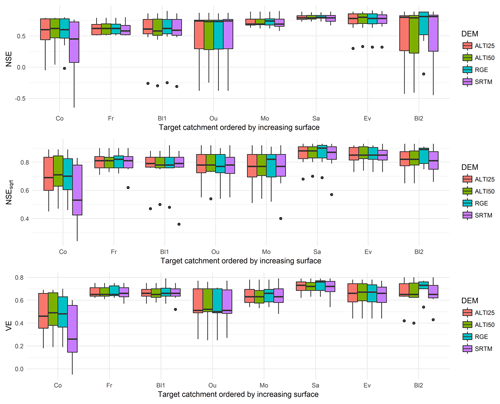
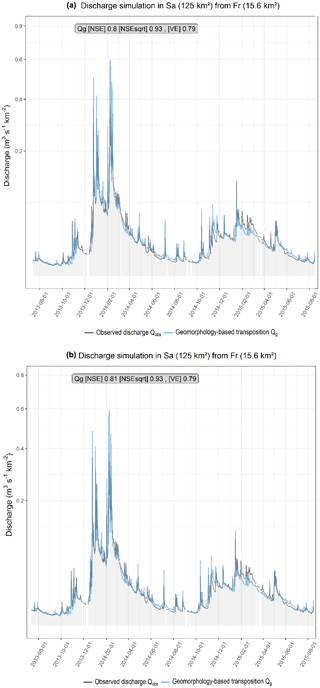
An overview of the results of simulation is displayed in Fig. 4 as a boxplot. For each basin and each DEM, all transpositions from other basins are gathered, for the continuous period 2012–2016, which allows a global comparison of the sensitivity to the DEM data source. Close and good results are obtained for all criteria and DEMs (median of NSE over 0.5). Lower values were assessed for Co, the smallest basin of the dataset (5 km²) using SRTM, which illustrates the importance of an accurate DEM for geomorphology-based modelling in headwater basins. However, a coarse DEM such as SRTM looks sufficient to perform geomorphology-based modelling on larger basins. The use of a high quality DEM such as RGE-5 m does not improve significantly the results. This could be explained by the local geomorphology characterized by low drainage densities and longer hillslopes, sufficiently captured by a regular DEM.

3.3 Hydrographs

Figure 5 displays an example (from Fr to Sa) of a discharge time series obtained by geomorphology-based transposition. Figure 5a and b is obtained from the high resolution national DEM (RGE, 5 m) and the medium resolution quasi-worldwide DEM (SRTM, 25 m), respectively. Identical scores are obtained for the 3 criteria, for these two neighbouring basins.

Figure 5 Discharge simulated series in pseudo-ungauged Sa (125 km²) from Fr (15.6 km²) between 8 January 2013 and 8 January 2015, using transfer functions extracted from (a) RGE (5 m) and (b) SRTM (25 m) – and observed series as a reference.

4 Conclusion

This study aimed to show the sensitivity of a robust geomorphology-based transposition framework: deconvolution of discharge time series in a gauged donor basin, generalisation of net rainfall towards another target basin and simulation of discharge time series in the (pseudo)-ungauged target basin, to the input DEM used to assess transfer functions. Simulations were performed in a systematic way between 8 basins selected from the center part of the Brittany region in the West of France, quite similar in hydroclimate and with slight differences in geology, and organized in a geographic neighbouring and partially nesting configuration. Regarding 3 criteria, NSE, NSE_sqrt and VE, good (median NSE ranging from 0.5 to 0.8) and consistent results were obtained for a 5-year simulation. The experiment shows that a coarse DEM such as SRTM, available internationally, gives similar results than a high-resolution DEM. The smallest basin Co (order 2) showed however the poorest results when using SRTM, which is explained by the limitation of this DEM to accurately describe the stream network geomorphology. The systematically good results obtained on larger basins (order 3 and more) in a data-rich region are a proof of concept which opens great perspectives for a PUB application in any location of the world, eventually with a poor discharge gauging density (Dixon et al., 2020), and with a high robustness regarding available geomorphometric data.