A shallow compaction model for Holocene Mississippi Delta sediments

The extensive loss of land elevation and the consequent exposure to flood hazards are seriously threatening the long-term survival of the Mississippi Delta. Shallow compaction of the top soil is one of the major components contributing to the relative sea level rise. In the last decades, more subsidence measurements have become available and recent studies demonstrate that compaction of Holocene strata is dominant. Here we propose a novel application aimed at modeling the present-day shallow compaction due to consolidation processes in the top soil. Soil compaction is properly computed and accounts for the large soil grain motion and the delayed dissipation of pore-water overpressure. The grain motion is described by means of a Lagrangian approach with an adaptive mesh where the grid nodes follows the accretion/compaction processes. Model calibration is obtained from stratigraphic and geochrology information collected at the Myrtle Grove Subsidence Superstation, where a nearly 40 m-deep sediment core that penetrates the entire Holocene succession allows testing model results over long (millennial) timescales. Model validation with available observations from rod surface-elevation table – marker horizon (RSET-MH) data enables the model to predict future scenarios.

1 Introduction

High rates of land subsidence are seriously threatening the long-term survival of the Mississippi Delta. The extensive loss of land elevation and the consequent exposure to flooding hazard put at significant risk vulnerable and highly populated deltaic areas. In the Mississippi delta reduction in aggradation plus accelerated compaction is substantially greater than global sea-level rise due to climate change (Syvitski et al., 2009). Shallow compaction of the top soil is one of the major components contributing to relative sea level rise (Törnqvist et al., 2008). In the last decades, more subsidence measurements have become available demonstrating that shallow compaction occurs mainly in the uppermost 5–10 m depth range (Jankowski et al., 2017).

Quantification of the spatio-temporal evolution of shallow deposits over the Holocene is crucial to predict land subsidence and to support decision making on sustainable coastal management. Here we propose a novel application aimed at modeling the present-day shallow compaction due to consolidation processes in the Mississippi delta. A groundwater flow simulator is coupled to a vertical geomechanical module to simulate the consolidation process and estimate the soil compaction. The model properly computes and accounts for large soil grain motion and the delayed dissipation of pore-water overpressure (Zoccarato and Teatini, 2017). This approach is suitable for applications in coastal environments where high rates of shallow compaction requires the adoption of a large soil deformation model (Zoccarato et al., 2018). The system of equations are solved with the aid of a Finite Element discretization by employing an adaptive mesh that follows the accreting and compacting movements of the soil grains.

Data available from a nearly 40 m-deep sediment core that penetrates the entire Holocene succession at the Myrtle Grove Subsidence Superstation (located at 29^∘37^′06.4^′′ N, 89^∘56^′47.8^′′ W) enables the calibration of the model results over millennial timescales (Bridgeman, 2018). Furthermore, a validation with available observations from rod surface-elevation table – marker horizon (RSET-MH) data (Jankowski et al., 2017) allows to predict future scenarios of subsidence. Finally, a restoration project planned for the next 10 years is simulated showing the impact of the artificial nourishment on the surface elevation change.

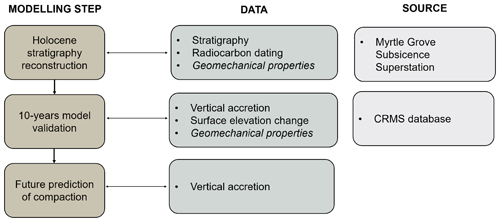
Figure 1 Modeling framework for the simulation of shallow compaction of Holocene sediments in the Mississippi delta. This study is subdivided into three modeling steps: Holocene stratigraphy reconstruction, model validation and future subsidence prediction. Each step is achieved using available data from the the Myrtle Grove Subsidence Superstation (Allison et al., 2016) and the Coastwide Reference Monitoring System (CRMS) (siteweb).

The paper is structured as follow. Section 2 describes the modeling approach with a brief overview of the governing equations and the data used for calibration and validation. Section 3 discusses the results and their possible implication for future subsidence predictions. Section 4 draws the conclusions to the paper.

2 Modeling approach

Figure 1 shows the modeling approach used to investigate the imprint of the Holocene sediments to actual rates of subsidence and provide for future predictions of relative sea level rise. The analysis is subdivided into three main steps, which define the objectives of this study. First, the simulation of the Holocene sequence deposition and the related quantification of the sediment compaction is carried out by modeling the accreting and consolidation processes occurred during the Holocene. This is done by first applying a decompaction model to compute the average accretion rates and then applying a geomechanical model of soil consolidation. The model is calibrated based on available data of litho-stratigraphy, radiocarbon dating, and hydro-geomechanical properties of the deposition units. Then, the model is validated against 10-years records of vertical accretion (VA) and surface elevation change (SEC). At this stage, prediction of subsidence rates are possible by employing the calibrated model. In particular, we simulate the land surface evolution due to a potential restoration project planned for the time period 2018–2028 CE to discuss the system response depending on the type of soil used for restoration. The importance of reconstructing the entire Holocene stratigraphy for subsidence evaluation and future predictions is crucial. Indeed, actual rates of subsidence depend on the lithology of the strata underlying the deposition of new sediments and the amount of consolidation occurred.

In the following a brief overview is given of the decompaction and geomechanical models and a description of the available data for calibration and validation purposes.

2.1 Decompaction model

Decompaction of the actual core allows to compute the average accretion rate ω over time spans during the Holocene (Kooi and de Vries, 1998). The result is then used as input into the geomechanical model. Decompaction is obtained by combining the relationship between void index e and depth z with an age-depth model. In this study, the relationship e-vs-z is available from oedometric tests collected at the Myrtle Grove core I. The age-depth model is obtained by collecting a number of ¹⁴C datings of organic remnants at different elevations within the sedimentary column (Bridgeman, 2018). The simplified chrono-stratigraphy is shown in Fig. 3a. Generally, decompacted thickness of the soil column presently comprised between depth z₁ and z₂ can be computed as (Gambolati and Teatini, 1998):

$$\begin{array}{}\text{(1)}& H_{\mathrm{0}}=(\mathrm{1}+e_{\mathrm{0}})\underset{z_{\mathrm{1}}}{\overset{z_{\mathrm{2}}}{\int }}{\displaystyle \frac{\mathrm{d}z}{\mathrm{1}+e\left(z\right)}}\end{array}$$

where e₀ is the initial void index. Denoting with t₁ and t₂ the deposition times of the sediments at depth z₁ and z₂, the average accretion rate within the time interval [t₁–t₂] is simply obtained as

$$\begin{array}{}\text{(2)}& \mathit{\omega }=H_{\mathrm{0}}/(t_{\mathrm{2}}-t_{\mathrm{1}})\end{array}$$

Figure 2 Schematic drawing of the approach taken in the geomechanical model where the consolidation equation is solved assuming large soil deformations.

2.2 Geomechanical model

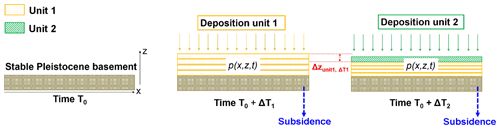
Accretion and consolidation of the Myrtle Grove core I is simulated with the aid of the numerical model NATSUB-2D developed by Zoccarato and Teatini (2017). The original formulation provides the solution of a coupled system of equations of 2-D groundwater flow and a 1-D consolidation process. A cartoon of NATSUB-2D modeling approach is shown in Fig. 2. The surface elevation changes according to accretion and consolidation processes, i.e., shallow subsidence. Over a compaction-free Pleistocene basement, deposition of unit 1 occurs during time ΔT₁ and the evolution of pore over-pressure p is computed by means of the groundwater flow model. Over-pressure dissipation causes the consolidation of the same unit. Then, over time ΔT₁ unit 2 deposits. Unit 2 is generally characterized by different hydro-geomechanical properties. Consolidation continues in unit 1, also because of the new load on its top, and starts in unit 2 as well. The model may also include the contribution of deep subsidence due to glacial isostatic adjustment, regional sediment loading, faulting or subsurface fluid withdrawal.

In this preliminary application, the flow equations are solved in a 1-D framework that represents the Holocene sequence of the Myrtle Grove core I. The rigorous equations of the 1-D flow in an elastic saturated compacting porous medium was originally developed in the late 70s (Gambolati, 1973a, b), where the hypothesis of infinitesimal displacement of the grains is relaxed and large soil deformations are accounted for introducing a geometric non-linearity. The governing equations of the groundwater flow and consolidation are described in detail in Zoccarato and Teatini (2017). The model solution depends on the hydro-geomechanical properties of the soils such as porosity ϕ, oedometric compressibility c_b, and hydraulic conductivity k_z. They are functions of the intergranular effective stress σ_z to account for their variability with the progressive deformation of the soil matrix, i.e., c_b, k_z, and ϕ diminish at increasing values of σ_z.

The numerical solution of the equations is implemented in NATSUB-2D by a Finite Element (FE) discretization, using a back Euler method for the time integration and a fixed-point iteration scheme to solve the material non-linearity. Moreover, a Lagrangian approach where a dynamic mesh follow the grains in their accretion/consolidation movements is employed to include large deformations without introducing a geometric non-linearity. A constant time step equal to 10 years has been adopted. A new finite element is added on the top of the column when the soil accretion amount to 10 cm.

2.3 Myrtle Grove Subsidence Superstation and CRMS database

Data available from the Myrtle Grove Subsidence Superstation (Allison et al., 2016) are used to calibrated the model outcome. The Superstation is a subsidence monitoring station near the Mississippi River, southeast of New Orleans. It provides insight into the stratigraphic and geotechnical properties of the Holocene succession with subsidence data collected at different spatio-temporal resolution by means of fiber-optic strainmeter/extensometer, GPS antennas and InSAR reflectors. In this study, the litho-stratigraphic description and the age-depth model of the Myrtle Grove I core (Bridgeman, 2018) has been used to model the formation of Holocene sequence. The core is about 40 m-deep and characterized by four main units of deposition. The age of the Holocene basal peat is estimated at 11.3 ka (where ka refers to kiloannum with respect to 2100 CE). Preliminary results obtained in this investigation consider only the upper two units, which mainly represent the entire core from the surface down to 35 m. This simplification is due to the lack of geochronological data at the bottom core. Moreover, the heterogeneity of unit 1 is not properly modeled assuming a homogeneous silty loam unit, except for the top core characterized by a ∼1.2 m-thick peat bed that represents the modern marsh (Bridgeman, 2018).

The behavior of e(z) in Eq. (1) and in the geomechanical model is described using a virgin loading model with

$$e\left(z\right)=e_{\mathrm{0}}-C_{\mathrm{c}}\text{log}{\mathit{\sigma }}_z$$

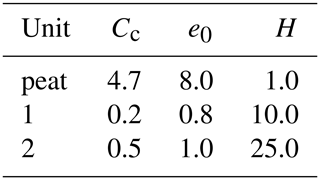
with C_c the compression index. The parameters e₀ and C_c are taken from oedometric tests performed on the Myrtle Grove I core (Bridgeman, 2018). The modeled Holocene sequence is shown in Fig. 3a. Table 1 reports the parameters C_c and e₀ of the virgin compression models and the actual thickness H of each deposition units.

Table 1 Parameters of the virgin compression model and actual thickness of the units characterizing the Holocene sequence.

VA and SEC data available from the Coastwide Reference Monitoring System (CRMS) (site 0276 nearby the Superstation) over the time period 2008–2017 are employed for validation purposes. The CRMS site is equipped with rod surface-elevation tablemarker horizon (RSET-MH) measurements. The database provides records over the last 10 years. VA and SEC allow for the calculation of shallow subsidence (SS) (Törnqvist et al., 2008):

$$\begin{array}{}\text{(3)}& \mathrm{SS}=\mathrm{VA}-\mathrm{SEC}\end{array}$$

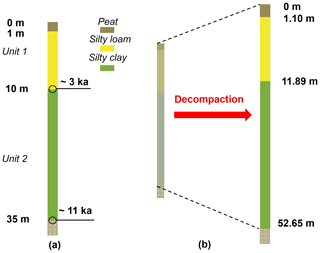
Figure 3 (a) Representation of the modeled Holocene sequence with available age-depth data. The first meter is characterized by a peat formation while unit 1 and 2 are modeled as silty loam and silty clay layers. (b) Result from the decompaction model where elevations of the compaction-free Holocene units are given.

3 Results

3.1 Reconstruction of the Holocene sequence

Figure 3b shows the result of the application of the decompaction model to peat formation, unit 1 and unit 2. The results provide a compaction-free thickness H₀ of about 1.10, 11.89 and 40.76 m, respectively. The corresponding deformations, computed as $(H_{\mathrm{0}}-H)/H_{\mathrm{0}}$, are 9 %, 16 %, and 40 %. Peat formation is the more compressible unit but provides the lower deformation because it lies at near-surface elevations yielding to low gravitational load of overlying sediments. The higher compaction is due to unit 2 having higher compressible material compared to unit 1 (see Table 1) and larger loading conditions. On average, the soil column undergoes a deformation of about 34 % over ∼11 ka.

Using the values of H allows computing the average accretion rates ω using Eq. (2). Values of ω equal to 1.1, 4.0, 5.1 mm yr⁻¹ for peat formation, unit 1 and 2, respectively, are used as input values to the geomechanical model, which allows to estimate the deposition and compaction processes of the Holocene sequence. The model outcome in terms of thicknesses is 1.07, 10.07 and 23.83 m for peat formation, unit 1 and unit 2, respectively, with a slight overestimation of compaction in unit 2. The mismatch between measured and reconstructed Holocene sequence is due to different assumptions in the decompaction and geomechanical models. Indeed, the compaction-free thickness resulting from decompaction does not take into account the process of overpressure dissipation, which is properly accounted for in the geomechanical model.

3.2 10-years validation

In this section, the calibrated model is used and further 10-years of accretion are simulated. The total simulation time spans 11.01 ka.

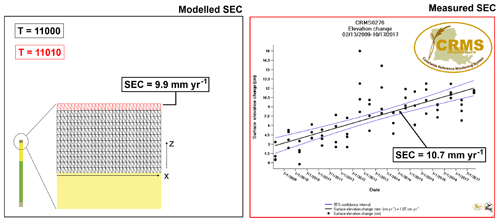
Figure 4 Validation of the model using the CRMS data at the 276 site where rate of surface elevation changes can be compared. The validation considers the 10-year period 2008–2017 CE. In the left subpanel the mesh grid is shown distinguishing by red color the new elements added over the top of column as consequence of the aggradation process. Right panel: CPRA (2020).

VA of 12.5 mm yr⁻¹ are obtained from records collected at site 276 of the CRMS database as an average value over the time period 2008–2017 CE. It is assumed that the deposition is similar to process responsible for the accretion of the near-surface sediments. Thus, the compressibility is derived from the same parameters of the peat formation (Table 1). Although only consolidation process is considered here, in peat formations other processes may play a role in vertical dynamics of surface change, such as those related to the loss of organic matter due to peat oxidation (Rao et al., 2016).

Figure 4 shows the comparison between model outcome and data. On the left subpanel of Fig. 4 a zoom of the mesh grid is provided where the grid nodes are shown only for the peat formation. In particular, the black mesh refers to the calibration period until 2008 CE, i.e., the simulation of the last 11 ka. The red FE represents the new elements added to the previous mesh due to aggradation over the period 2008–2017 CE. Each mesh row is characterized by different element thickness as direct consequence of the ongoing consolidation process with elements at the bottom of the peat formation slightly more compacted than the element at the top. Notice that the simulated process is 1-D even tough the computational mesh is 2-D.

Modeled SEC rate is 9.9 mm yr⁻¹, i.e., 7.5 % lower than the corresponding measured value of 10.7 mm yr⁻¹. Positive SEC means the surface elevation is accreting. SS is evaluated using Eq. (3). Measured SS equals 1.8 cm over 10-years validation whereas the model SS estimation is 2.6 cm. The model overestimation may probably due to the assumption on the characterization of the peat formation. However, the model seems to predict quite well the system response under the above-mentioned assumptions.

3.3 Predictions of subsidence as result of marsh restoration

In the Louisiana coast, restoration projects are carried out by the Coastal Protection and Restoration Authority (CPRA). Among different types of restoration projects, marsh creation and diversion implies material handling by sediment dredging and placement in the restoration area or by diversion of sediment and fresh water from the Mississippi and Atchafalaya Rivers into adjacent basins (http://coastal.la.gov, last access: 31 August 2019). In both cases, the type of material used for restorations along with the knowledge of the above-ground behavior of the Holocene sediments are crucial in terms of net accretion rate. Here we simply investigate the effect of restoration by introducing new sediments above the Holocene sequence with a vertical accretion rate of 10 mm yr⁻¹ over then 10-years period 2018–2028 CE. The parameters of sediments used for the restoration correspond to those of unit 1 (Table 1). With such an hypothesis, the 100 mm of VA yields to SEC =1 and SS =99 mm. It means that only 1 % of deposition provides net accretion to the system and the rest undergoes compaction. This means that the deposition of heavy relatively stiff (silty loam) soil over light and compressible peat causes a compaction of this latter that almost totally offset the thickness of the former deposited above it.

4 Conclusions

In this paper, the numerical modeling of the long-term accretion/compaction of the Mississippi delta at a representative site is carried out by employing a coupled groundwater-consolidation model. A 1-D approach is considered in this preliminary investigation. Model calibration is carried out by using available data from the Myrtle Grove Subsidence Superstation Model where detailed information is available.

The model is validated against data of vertical accretion and surface elevation change from the CRMS database (site 0276 located nearby the surpstation). The model can be used as supporting tool to design and manage projects of protection and restoration, as it allows for predictions of subsidence under future conditions of the coastal wetlands. Improvements to the present model are expected by detailing the description and simulation of the Holocene stratigraphy with the ultimate scope at simulating the spatial heterogeneity in a 2-D framework.

Moreover, at this stage of the investigation the results are given in a deterministic framework. It is clear that errors associated with the geomechanical parameters, the average accretion rate, the geochronological Holocene reconstruction, and the mathematical model itself are sources of uncertainty for future predictions. Proper analysis of the uncertainty propagation from model input to output will be further considered.