Numerical simulation of land subsidence caused by subway train vibration using PFC

Subsidence induced by human activity and urbanization is distributed in an area or along a line. In Shanghai, China, land subsidence is distributed along the belt near a subway line. The subsidence is caused by train vibration as well as regional land subsidence and other engineering activity. In order to figure out the mechanical response of the tunnel surroundings, the PFC2D software based on a discrete element method is introduced to simulate a section of the metro tunnel. The linear contact bond model was employed to reflect the characteristics of clay. Based on the analysis of stress and settlement caused by dynamic cyclic loading, the mechanical response law and subsidence mechanism were investigated. In addition, the influence of frequency on settlement was also analyzed: the greater the frequency, the more particles were rearranged and the larger the settlement. The fraction of sliding contacts was introduced to explain this phenomenon. The results can be used to understand, predict and control land subsidence to protect the geological environment.

1 Introduction

With the fast development of urbanization in China, more and more subway lines will be constructed to relieve traffic pressure. It is inevitable for subway lines to encounter a soft soil foundation and surrounding rock. The train vibration load is a kind of long-term cyclic load, which can cause the accumulation of settlement and contribute to regional land subsidence. Large subsidence of soft foundation often occurs under repeated loading of subway trains, which may induce cracks in adjacent buildings (Tang et al., 2008; Zhang and Li, 2015). According to Ye et al. (2007) and Liu et al. (2009), the settlement of a section exceeds 200 mm during the operation of the metro line 1 in Shanghai. Therefore, lots of scholars have studied the dynamic response of soil under cyclic loading. Seed et al. (1955) investigated the strength and deformation of compacted clay by a series of triaxial compression tests in the early stage. Yasuhara et al. (1992) studied the influences of undrained cyclic loading on clay behavior using triaxial tests. Based on cyclic triaxial tests results, Zhou et al. (1996) proposed an empirical model for predicting the residual deformation of soft clay, which can be used to estimate additional settlement of soft clay foundation under partially drained cyclic loading. Chai and Miura (2002) presented a prediction method of road on soft subsoil with a low embankment under a traffic load. Xie et al. (2008) considered the factors of soil constitutive modeling, tunnel-foundation structure modeling and simulation of the subway load to investigate the dynamic response of foundation soil. Zhang et al. (2011) analyzed the dynamic response and settlement law of foundation soil under different loading numbers based on a three-dimensional finite element method. Jiang et al. (2013) analyzed the triaxial test results of saturated soft clay and proposed a new empirical model to simulate the cumulative plastic strain of soft clay under K0-consolidated condition. Lei et al. (2019) used the three-dimensional finite element method to study settlement law of foundation soil under different train velocities. The above research is focused on the dynamic response of foundation soil under cyclic loading, and less analysis of settlement mechanism was performed, especially from the microcosmic point of view.

In order to investigate the settlement mechanism of soft soil under cyclic loading, a discrete element method (DEM) was employed in this paper to establish subway tunnel models, and a semi-sinusoidal load was selected as the subway vibration load. The settlement mechanism and response law were analyzed by monitoring the changes of microscopic parameters, which is significant for the prediction of long-term subsidence of the subway foundation.

2 Numerical model

The radius of the subway tunnel is 3 m in this model, and 44 m in length to keep a distance of 3 times the tunnel diameter to the boundary. The tunnel depth is 10 m, and the width is 38 m. Due to the restricted computing capability, it is scarcely possible to simulate the clay with real particle size based on DEM. In addition, according to Zhou et al. (2009), the appropriate enlargement of average particle size did not affect the macroscopic mechanical properties of the sample when the calculated particle number exceeded 2000 based on DEM. The particle radii are uniformly distributed between the minimum and maximum values of 0.06 to 0.1 m, respectively. The total number of particles are 66 405. The linear contact bond model is employed in the model to simulate typical clay, and its parameters are shown in Table 1.

Table 1 Material parameters of numerical simulation.

There are many factors that affect the vibration frequency of traffic loading, such as train speed, train type, etc. It is difficult to determine the real frequency for traffic loading. According to published results, different vibration frequencies were used to investigate the dynamic response of subsurface layers under traffic loading. McDowell et al. (2005) performed laboratory simulation of train loading at a frequency of 3 Hz. Zheng and Liu (2007) carried out field testing on a section of Shanhgai metro line 1, and it was found that the vibration frequency was mainly at a low frequency of 10 Hz. Tang et al. (2008) studied the characteristics of deformation of saturated soft clay in Shanghai under a subway load with 2.5Ḣz frequency. Aursudkij et al. (2009) found that the typical loading frequency of traffic loading in the track is normally around 8–10 Hz for a normal train (by assuming axle wheel spacing of 2.6 m and train speed of 75–94 km h⁻¹) and may reach 30 Hz for a high-speed train. The average value (6 Hz) of lower limit frequencies from the above references was adopted in this paper, which can represent the average level of traffic loading to some extent. Hence, the semi-sinusoidal load with frequency 6 Hz and dynamic stress amplitude 20 kN simulates train vibration loading (Pu et al., 2019).

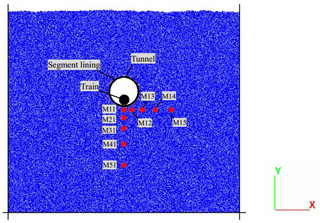
In order to study the spatial distribution law of stress caused by cyclic loading, the stresses at different distances from the central line of the tunnel were measured with M11 (0 m), M12 (1.5 m), M13 (3.5 m), M14 (6 m) and M15 (9 m) in the horizontal direction and M11 (1 m), M21 (2 m), M31 (4 m), M41 (7 m) and M51 (11 m) in vertical direction. The section model of the subway tunnel is shown in Fig. 1.

Figure 1 Section model of the metro tunnel.

3 Results and discussions

There are lots of factors that affect the vibration frequency of traffic loading, such as train speed, train type, etc. It is difficult to determine the real frequency for traffic loading. According to published results, different vibration frequencies were used to investigate the dynamic response of subsurface layers under traffic loading. McDowell et al. (2005) performed laboratory simulation of train loading at a frequency of 3 Hz. Zheng and Liu (2007) carried out field testing on a section of Shanhgai metro line 1, and it was found that the vibration frequency was mainly at a low frequency of 10 Hz. Tang et al. (2008) studied the characteristics of deformation of saturated soft clay in Shanghai under subway load with 2.5 Hz frequency. Aursudkij et al. (2009) found that the typical loading frequency of traffic loading in the track is normally around 8–10 Hz for a normal train (by assuming axle wheel spacing of 2.6 m and train speed of 75–94 km h⁻¹) and may reach 30 Hz for a high-speed train. The average value (6 Hz) of lower limit frequencies from the above references was adopted in this paper, which can represent the average level of traffic loading to some extent. Hence, the semi-sinusoidal load with frequency 6 Hz and dynamic stress amplitude 20 kN simulates train vibration loading (Pu et al., 2019).

In order to study the spatial distribution law of stress caused by cyclic loading, the stresses at different distances from the central line of the tunnel were measured with M11 (0 m), M12 (1.5 m), M13 (3.5 m), M14 (6 m) and M15 (9 m) in the horizontal direction and M11 (1 m), M21 (2 m), M31 (4 m), M41 (7 m) and M51 (11 m) in vertical direction. The section model of subway tunnel is shown in Fig. 1.

3.1 X-direction stress distribution

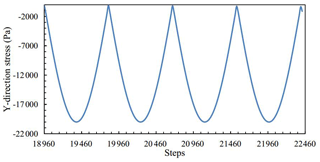
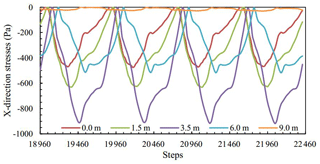
X-direction stress of M11, M12, 13, M14 and M15 was measured and plotted in Fig. 3 between the steps from 18 960 to 22 460, and the matched cyclic loading is shown in Fig. 2.

Figure 2 Cyclic loading at the bottom of the tunnel.

Figure 3 X-direction stresses at different distances from the central line of the tunnel.

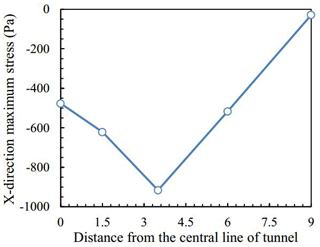
The variations of x-direction stresses at different distances from the central line of the tunnel were basically the same (Fig. 3), which were similar to the cyclic loading at the bottom of the tunnel. The maximum stress amplitude was shifted to the right with increasing distance from the central line of the tunnel. According to Fig. 4, a critical value existed in x-direction maximum stress with increasing distance from the central line of the tunnel. When the distance was less than the critical value, the x-direction maximum stress increased with increasing distance while maximum stress reduced with growing distance. In addition, the x-direction maximum stress amplitude was pretty small when the distance exceeded 9 m.

Figure 4 Variations of x-direction maximum stress at different locations.

Figure 5 Y-direction stresses at different distances from the bottom of the tunnel.

3.2 Y-direction stress distribution

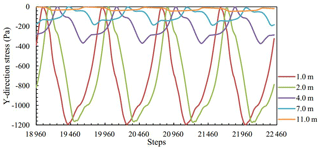
Y-direction stress of M11, M21, M31, M41 and M51 was measured and plotted in Fig. 5 from step 18 960 to step 22 460, and the matched cyclic loading is shown in Fig. 2.

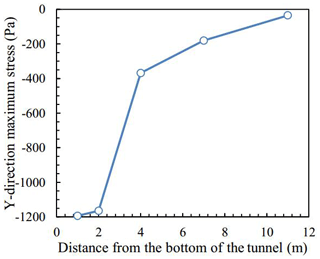
From Fig. 5, the changes of y-direction stress with increasing depth was similar to that of x-direction stress. They were similar to the semi-sinusoidal load with the same frequency. The difference was that they have different dynamic stress amplitudes with increasing depth. Figure 6 plots the variation of y-direction maximum stress with increasing depth from the bottom of the tunnel, which shows the maximum stress increased nonlinearly along increasing depth generally. The y-direction maximum stress increased sharply when the distance was between 2 and 4 m, which was similar to the characteristics of x-direction maximum stress at the same distance. Therefore, the maximum stress of the tunnel surroundings under cyclic loading was not at the nearest position, but a certain distance from the tunnel.

Figure 6 Variations of y-direction maximum stress with different locations.

Figure 7 Cumulative settlement under different cyclic times.

3.3 Y-direction cumulative settlement

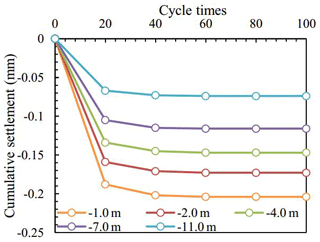
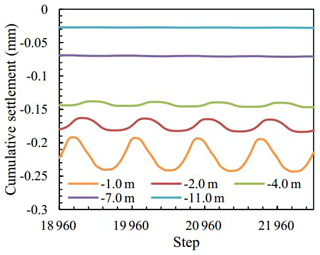
The cumulative settlement at different depths with increasing cyclic times is shown in Fig. 7. With increasing distance from the bottom of the tunnel, cumulative settlement reduced gradually, and the subsidence tendencies were basically the same. The settlement was large in the early stage and then gradually smoothed. The maximum cumulative settlement at M11 was 0.204 mm, while the settlement at M51 was only 0.074. Figure 8 presents the cumulative settlement curves under different depths between 18 960 and 21 960 steps. The shapes of cumulative settlement curves were basically both influenced by cyclic loading. However, the amplitude of cumulative settlement varied greatly under different depths. When the depth from the bottom of the tunnel was greater than 7 m, the curve of cumulative settlement approached a straight line, which means cyclic loading has little effect.

Figure 8 Cumulative settlement curve with steps.

Figure 9 Cumulative settlement with different frequencies.

Figure 10 Fraction of sliding contacts with different frequencies.

3.4 Cumulative settlement and mechanism

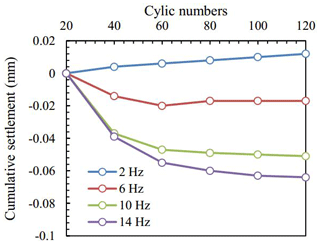
The cyclic numbers 20 was taken as the starting point, and M11 was selected as the research location. The cumulative settlement corresponding to different frequencies is plotted in Fig. 9, where the cumulative settlement increases with increasing frequency. When the frequency was 2 Hz, the cumulative settlement was a positive value, which means rebound occurs and there was no settlement.

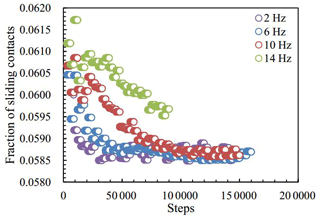
The cumulative settlement of soil was mainly caused by the rearrangement of particles without considering the fragmentation. From a microscopic point of view, fraction of sliding contacts, F_s, can characterize the sliding of particles to some extent (Huang et al., 2015), and it can be expressed as follows:

$$\begin{array}{}\text{(1)}& F_{\mathrm{s}}={\displaystyle \frac{N_{\mathrm{s}}}{N}},\end{array}$$

where N_s represents the number of sliding contacts and N is the number of total contacts. The fractions of sliding contacts in soils with different frequency are shown in Fig. 10. The fraction of sliding contacts increased with the increase in frequency. This is similar to the relationship between cumulative settlement and frequency. The larger the fraction of sliding contacts, the more particles were rearranged and the larger the settlement.

4 Conclusions

Based on DEM, a section model of a subway tunnel was established, and semi-sinusoidal load was used to simulate the vibration load of a subway train. By analyzing stresses and settlement caused by cyclic loading, the mechanical response law and settlement mechanism were investigated. With the increasing distance from the central line and bottom of the tunnel, both the stresses and settlement are reducing gradually, while they have similar shape to the cyclic loading. In addition, frequency has an influence on cumulative settlement. The greater the frequency, the more particles were rearranged and the larger the settlement. The phenomenon is reflected in the fraction of sliding contacts. Therefore, the reduction of train speed is helpful to control subsurface subsidence under traffic loading.