Three-dimensional fully coupled study of groundwater seepage and soil deformation under the action of cyclic pumping and recharge

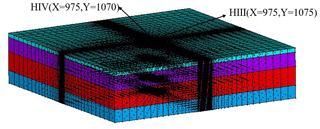
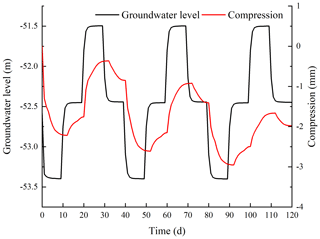
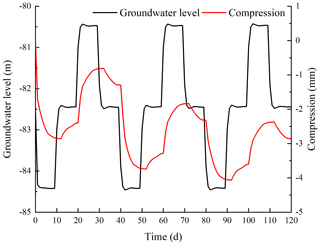
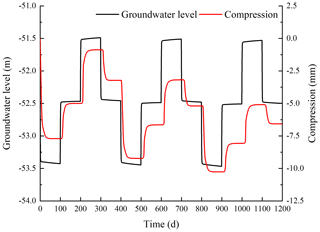
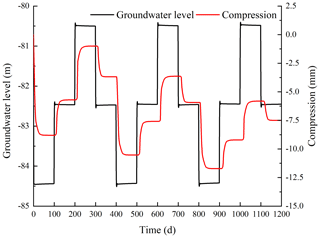
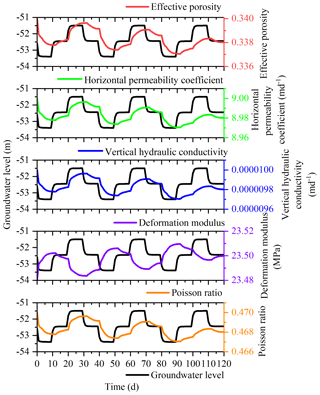
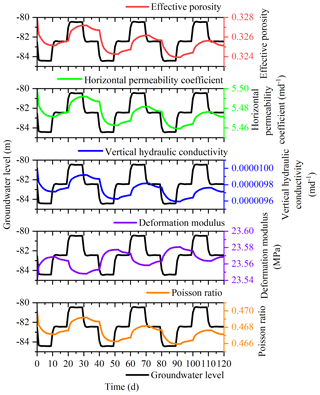
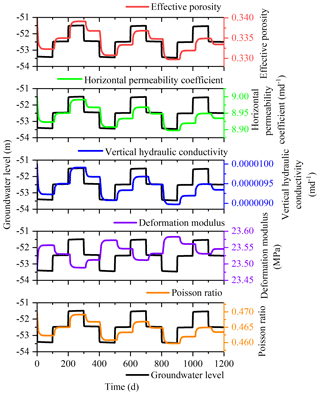
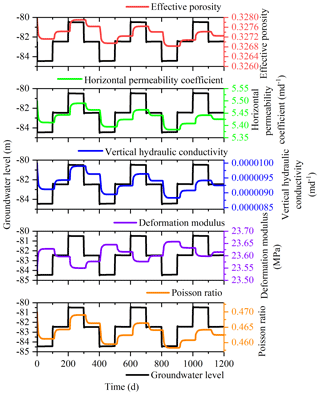
This study was undertaken in order to accurately analyze the land subsidence that is caused by the change in the seepage and stress fields during the pumping and recharge of groundwater. Based on Biot's consolidation theory and groundwater seepage theory (combined with theory regarding the nonlinear rheology of soil), the constitutive relationship of soil was extended to viscoelastic plastic; concurrently, considering the dynamic changes in hydraulic parameters and soil mechanical parameters, a three-dimensional fully coupled model of groundwater seepage and soil deformation was established. Using the groundwater recycling pumping and recharge test conducted by Land Subsidence Monitoring and Early Warning Center in Cangzhou City as an example, the site was divided into four loose porous aquifers. A constantly circulating pumping–recharge flow was simulated numerically, and numerical simulation was carried out on the third and fourth confined aquifers. The influence of groundwater seepage on soil deformation was analyzed, and the variation in hydraulic parameters and soil mechanical parameters were studied under the influence of the abovementioned cyclic pumping and recharge. The results show that soil deformation lags behind the change in the groundwater level, and that permanent residual deformation of soil is produced by water level fluctuations during groundwater pumping–recharge cycles. The effective porosity, the permeability coefficient and the Poisson ratio are positively correlated with the water level fluctuation in groundwater pumping–recharge cycles, whereas the modulus of deformation is negatively correlated with the water level fluctuation in groundwater during this process. All parameters change, and this change is permanent. The simulated results are in good agreement with the measured values.

1 Introduction

In recent years, groundwater recharge has become an emerging method for controlling the groundwater level (causing it to drop substantially) and alleviating the development of land subsidence. It uses artificial measures to inject water from surface water or other sources into the ground to fill the groundwater funnel. Recently, experts have began exploring the changing characteristics of the soil state during groundwater recharge. In a preliminary study, Zhu (1982) explored the deformation characteristics of soil mass during pumping and recharge under unidirectional osmotic pressure conditions. Su (1979) put forward the concept of the “swell–shrinkage ratio” and analyzed the residual denaturation characteristics of each soil layer under the action of pumping and recharge. Wu and Miao (1995) and Miao et al. (1996) proposed a linear viscoelastic stress–strain constitutive model suitable for revealing the mechanics of pumping compaction and recharge expansion of the aquifer soil skeleton. Zhang et al. (2006) and Wu et al. (2009) constructed a model in which the spring body and Bingham body were connected in parallel and then another spring body was connected to the series; this model can obtain the deformation parameters of the sand layer and then, in turn, allow for the study of the trend in the variation of land subsidence. Phien-Wej et al. (1988) expounded the relationship between groundwater seepage and land subsidence using a single-well recharge test. In this paper, the stress–strain relationship of soil is extended to viscoelastic plasticity, a three-dimensional fully coupled model of groundwater seepage and soil deformation is established, the relationship between the aquifer water level and compressive deformation in the process of pumping and recharge is studied quantitatively, and the dynamic response mechanism of the aquifer water level and compressive deformation during the process of pumping and recharge is revealed.

2 Fundamental theory

2.1 Biot's consolidation theory

Based on the effective stress principle, Biot derived a three-dimensional consolidation equation that correctly reflects the relationship between pore water pressure dissipation and soil skeleton deformation (Luo and Zeng, 2011):

$$\left\{\begin{array}{l}-G{\mathrm{\nabla }}^{\mathrm{2}}{\mathit{\omega }}_x-\frac{G}{\mathrm{1}-\mathrm{2}v}\frac{\partial }{\partial x}\left(\frac{\partial {\mathit{\omega }}_x}{\partial x}+\frac{\partial {\mathit{\omega }}_y}{\partial y}+\frac{\partial {\mathit{\omega }}_z}{\partial z}\right)+\frac{\partial u}{\partial x}=\mathrm{0}\\ -G{\mathrm{\nabla }}^{\mathrm{2}}{\mathit{\omega }}_y-\frac{G}{\mathrm{1}-\mathrm{2}v}\frac{\partial }{\partial y}\left(\frac{\partial {\mathit{\omega }}_x}{\partial x}+\frac{\partial {\mathit{\omega }}_y}{\partial y}+\frac{\partial {\mathit{\omega }}_z}{\partial z}\right)+\frac{\partial u}{\partial y}=\mathrm{0}\\ -G{\mathrm{\nabla }}^{\mathrm{2}}{\mathit{\omega }}_z-\frac{G}{\mathrm{1}-\mathrm{2}v}\frac{\partial }{\partial z}\left(\frac{\partial {\mathit{\omega }}_x}{\partial x}+\frac{\partial {\mathit{\omega }}_y}{\partial y}+\frac{\partial {\mathit{\omega }}_z}{\partial z}\right)+\frac{\partial u}{\partial z}=-\mathit{\gamma }\\ -\frac{\partial }{\partial t}\left(\frac{\partial {\mathit{\omega }}_x}{\partial x}+\frac{\partial {\mathit{\omega }}_y}{\partial y}+\frac{\partial {\mathit{\omega }}_z}{\partial z}\right)\\ +\frac{\mathrm{1}}{{\mathit{\gamma }}_{\text{w}}}\left[\begin{array}{l}\frac{\partial }{\partial x}\left(k_x\frac{\partial u}{\partial x}\right)+\frac{\partial }{\partial y}\left(k_y\frac{\partial u}{\partial y}\right)\\ +\frac{\partial }{\partial z}\left(k_z\frac{\partial u}{\partial z}+{\mathit{\gamma }}_{\text{w}}\right)\end{array}\right]+W=\mathrm{0}.\end{array}\right.$$

In the above formula, G is the shear modulus; ω_x, ω_y and ω_z are displacement components in three different directions; u is the pore water pressure; γ is the weight of soil; γ_w is the weight of water; and k_x, k_y, k_z are permeability coefficients in three different directions.

2.2 Biot's consolidation finite element equation

In this study, the finite element governing equation of Biot's consolidation theory is established using the Galerkin weighted residual method, where displacement is replaced by a displacement increment in Δt, pore water pressure is expressed in its full form, and Biot's three-dimensional finite element equation is deduced. Thus,

$$\begin{array}{rl}& \left[\begin{array}{cc}\mathbf{K}& \mathbf{C}\\ {\mathbf{C}}^T& \mathit{\theta }\mathrm{\Delta }t\mathbf{H}+G\end{array}\right]\left\{\begin{array}{c}\mathrm{\Delta }\mathit{\delta }\\ u_{i(n+\mathrm{1})}\end{array}\right\}=\\ & \left\{\begin{array}{c}\mathrm{\Delta }F+C{u}_{i\left(n\right)}\\ \mathit{\theta }\mathrm{\Delta }t\mathrm{\Delta }\mathbf{Q}-\left(\mathit{\theta }\mathrm{\Delta }t\mathbf{H}+G\right)u_{i\left(n\right)}\end{array}\right\}\end{array},$$

where, K is the infiltration flow matrix, C is the elastoplastic flexibility matrix, Δδ is the joint displacement increment, ΔF is breaking the increment of the criterion function, ΔQ is the traffic increment matrix, H is the water level matrix and θ is the lode angle.

A fixed head boundary is used in the simulation. The initial displacement value is set to zero, and the displacement of the three directions is also zero in this simulation. According to the abovementioned mathematical model (solving the model using the Galerkin finite element method), a three-dimensional fully coupled numerical analysis program for groundwater seepage and soil deformation has been developed using the Fortran 95 language.

Table 1 Parameter zones and values.

3 Application example

3.1 Conceptual model

The study area is located in the urban area of Cangzhou City, Hebei Province. The terrain is low and flat. A four-layer aquifer model with a length of 2000 m, a width of 2000 m and a height of 400 m is established. This four-layer model can be divided into four aquifer groups according to the layer order from top to bottom. The first aquifer formation is from the Holocene, its floor is 30 m deep, and its lithology is dominated by fine sand and silt. The second aquifer formation is from the Upper Pliocene, its floor is 170 m deep, and its lithology is mainly medium sand and coarse medium sand. The third aquifer group is from the Middle Pleistocene, its floor is 290 m deep, and its lithology is mainly sub-clay and clay. The fourth aquifer group is from the Pleistocene, its floor is 400 m deep, and the lithology is mainly sub-clay and clay. An eight-node hexahedral element is adopted for discretization. The plane is divided into 3672 units, which results in a total of 14 688 units. Each layer is a parameter partition, which results in a total of four parameter partitions. The boundary of the model is generalized to a definite head boundary, the bottom of which is an impermeable boundary, and there is no hydraulic connection between the bottom of the model and the aquifers. The three-dimensional mesh of the model is shown in Fig. 1, and the zones and values of the parameters are shown in Table 1.

Figure 2 Compressed volume and water level with stress period in the third confined aquifer group under the first pumping and recharge scheme.

Figure 3 Compressed volume and water level with stress period in the fourth confined aquifer group under the first pumping and recharge scheme

Figure 4 Compressed volume and water level with stress period in the third confined aquifer group under the second pumping and recharge scheme.

Figure 5 Compressed volume and water level with stress period in the fourth confined aquifer group under the second pumping and recharge scheme.

Figure 6 Parameter and water level with stress period in the third confined aquifer group under the first pumping and recharge scheme.

4 Model computation and analysis

4.1 Settlement calculation and analysis

Three rounds of pumping–recharge cycles are carried out in the model. Each round is divided into four stages, totaling 12 stages, and each stage has the same time step. The first scheme uses 10 d as a stress period and one stress period is a time step, resulting in 12 stress periods. The second scheme uses 100 d as a stress period and one stress period as a time step, resulting in 12 stress periods. Pumping wells and recharging wells have the same well locations, which are located in the third and fourth aquifer groups, respectively; the wells are referred to as “Well HIII” and “Well HIV”, and the two wells are in unit 9959 and unit 13 575, respectively. The pumping time is the first stress period, the fifth stress period and the ninth stress period; the recharging time is the third stress period, the seventh stress period and the eleventh stress period. During the remaining stress periods, wells HIII and HIV are closed and the water level is restored. The single-well pumping and recharging water flow is 200 m³ d⁻¹.

The compression and water level of the third and fourth aquifers under the two pumping and recharge schemes vary with stress period as shown in Figs. 2–5.

4.2 Calculation and analysis of parameters

During the pumping and recharge process, the seepage field of groundwater, the state of soil, and the mechanical properties all change accordingly. Whether the dynamic change process of the parameters corresponds to the consolidation process of soil depends on the correctness of the model. The calculation results from the model are pore water pressure. The parameters and the groundwater level with respect to stress period under the two pumping–recharge schemes are shown in Figs. 6–9.

Figure 7 Parameter and water level with stress period in the fourth confined aquifer group under the first pumping and recharge scheme.

Figure 8 Parameter and water level with stress period in the third confined aquifer group under the second pumping and recharge scheme.

Figure 9 Parameter and water level with stress period in the fourth confined aquifer group under the second pumping and recharge scheme.

5 Conclusions

The main outcomes of this work are as follows:

1. Based on Biot's consolidation theory, a three-dimensional fully coupled model of groundwater seepage and soil deformation is established that fully considers the changes in the groundwater seepage field and soil mechanical parameters during soil deformation. The calculation results of this model are in line with the real situation, and its accuracy is better than other numerical models.

2. The soil deformation calculated by the three-dimensional fully coupled model of groundwater seepage and soil deformation lags behind the change in the water level. After the three pumping–recharge cycles, the water level is restored to the initial water level, and there is residual settlement of the soil layer, which is in accordance with the actual situation.

3. The trend in the variation of the effective porosity, the permeability coefficient, the deformation modulus and the Poisson ratio corresponds to the deformation trend in soil. The groundwater level changes periodically with the development of pumping and recharge: first decreasing, restoring and rising, and then rising, restoring and falling. Soil deformation shows a trend where it first compresses and then rebounds. The total trend in the variation of the effective porosity, the permeability coefficient and the Poisson ratio first decreases and then increases. The overall trend in the variation of the deformation modulus increases first and then decreases. However, all parameters lag behind the change in groundwater level.