Blending measurements and numerical models: a novel methodological approach for land subsidence prediction with uncertainty quantification

The use of numerical models for land subsidence prediction above producing hydrocarbon reservoirs has become a common and well-established practice since the early '90s. Usually, uncertainties in the deep rock behavior, which can affect the forecast capability of the models, have been taken into account by running multiple simulations with different constitutive laws and mechanical properties. Then, the most uncertain parameters were calibrated to reproduce available subsidence measurements. The objective of this work is to propose a novel methodological approach for land subsidence prediction and uncertainty quantification by integrating the available monitoring information in numerical models using ad hoc Data Assimilation techniques. The proposed approach allows to: (i) train the model with the available data and improve its accuracy as new information comes in, (ii) quantify the prediction uncertainty by providing confidence intervals and probability measures instead of deterministic outcomes, and (iii) identify the most appropriate rock constitutive model and geomechanical parameters. The methodology is tested in synthetic models of production from hydrocarbon reservoirs. The numerical experiments show that the proposed approach is a promising way to improve the effectiveness and reliability of land subsidence models.

1 Introduction

The interest and capability of analyzing real world phenomena in a stochastic way have increased in recent years. Focusing on land subsidence, deterministic studies do not allow to take care of uncertainties that unavoidably affect the characterization of the porous medium, e.g., the choice of the constitutive law and values of the governing mechanical parameters. A way to address this issue relies on the integration of Data Assimilation (DA) techniques into the numerical model, in order to train the model through the available measurements and improve the reliability and accuracy of the solution by reducing the uncertainties. In petroleum engineering, DA approaches have been originally used for history matching purposes, with recent applications for subsidence prediction (Baù et al., 2016; Fokker et al., 2016; Zoccarato et al., 2016). In a very recent work by Gazzola et al. (2019), different kinds of DA approaches are combined in a novel robust methodological approach for the stochastic analysis of land subsidence. It allows for the quantification and reduction of uncertainties affecting this process, with the aim to build more realistic and reliable models. Here, that idea has been further developed and improved with the definition of a three-stage workflow that has been applied to a synthetic model of land subsidence above a producing hydrocarbon reservoir, in order to investigate strengths, weaknesses and potentials. The procedure is based on the generation of many ensembles of Monte Carlo realizations, differing, for example, for the constitutive law that describes the porous medium behavior and the values of the geomechanical parameters. Then, the methodology consists of: (i) a first model diagnostic stage based on the mismatch between the model outcomes and the available measurements, which allows to select the most appropriate ensemble; (ii) a Bayesian approach, i.e. Red Flag (RF) technique, for the identification of the parameter combinations with the highest probability of occurrence, and (iii) an ensemble-based DA technique, i.e. Ensemble Smoother (ES), which updates the model, allowing for a reduction and quantification of the uncertainties. The aim of this methodology is to study land subsidence in a stochastic way, providing confidence intervals and probability measures instead of deterministic outcomes. This is possible by training the model with the available measurements and improving its accuracy as new information comes in, allowing for the definition of the most appropriate rock constitutive law and geomechanical parameters, which are not known a priori. The proposed methodology has been applied to a synthetic realistic test case, considering a hydrocarbon production program for an off-shore reservoir and a GPS station that records displacement measurements. The numerical experiments show the promising potential of the proposed workflow, which appears to be a useful tool to improve the effectiveness and reliability of land subsidence models, also in a predictive sense.

The paper is organized as follows. First, the methodological approach is described in detail, then the synthetic, but realistic, test case is presented with a discussion of the outcomes of every step of the proposed workflow. Finally, a few conclusive remarks close the presentation.

2 Methodological approach

At the very beginning of a land subsidence study, the number of available pieces of information concerning the deep rock behavior is usually low. For example, the most appropriate constitutive law that defines the behavior of the porous medium is generally unknown and the mechanical properties of the porous medium, e.g. stiffness or anisotropy, can be estimated only within a variability range by laboratory tests and preliminary in-situ analyses. Consequently, the first step for a stochastic subsidence analysis is to propagate all these input uncertainties to the subsidence prediction, that is the output of the geomechanical model. This is done by the generation of many forecast ensembles of Monte Carlo realizations for each constitutive law that could be suitable to describe the behavior of the porous medium, and considering different variability ranges for the main mechanical parameters. When the production program starts, displacement records are collected and used to train the model through different DA approaches in order to reduce the uncertainties and make the analysis more accurate and reliable. In particular, following the methodological approach proposed in Gazzola et al. (2019), a Bayesian approach, i.e., RF technique, and a smoother formulation are suggested. Here, a preliminary model diagnostic is added, in order to evaluate the most suitable ensemble for the successive and more expensive DA techniques.

A way to validate the ensemble is the χ²-test, as used in Chen and Oliver (2013), Fokker et al. (2016) and Oliver and Alfonzo (2018). This procedure is based on the fact that, for linear problems, the minimum of the mismatch between the model result and the available measurements produces a χ² distribution with degrees of freedom equal to the number of measurements (Tarantola, 2005).

After that, a cheap and fast analysis of the forecast ensembles can be performed by the RF technique, as introduced in Nepveu et al. (2010). It is a statistical approach that computes the probability of every Monte Carlo realization by combining prior information with the likelihood of the measurements, without solving the inverse problem.

Finally, the ES technique is applied, a non-sequential DA algorithm originally proposed by Van Leeuwen and Evensen (1996). It is an ensemble-based technique used to update both state variables and model parameters and evaluate their uncertainties by combining prior information, measurements, and the solution of the forward model. Results are optimal when the probability distribution of uncertain parameters is Gaussian (Van Leeuwen and Evensen, 1996). The ES has been widely used in subsidence applications, some recent examples are Baù et al. (2016), Fokker et al. (2016) and Zoccarato et al. (2018). The analyses that follow are carried out with the ES implementation according to the approach by Evensen (2003). The outcomes of the ES application are evaluated by two performance indices, the average absolute error (AE) and the average ensemble spread (AES) as proposed by Hendricks Franssen and Kinzelbach (2008) and used in Zoccarato et al. (2016). The AE index is a measure of the algorithm capability to approach the truth, as it compares the model outcome with the true reference value for each observation. This index can be computed only in a synthetic case where the true reference is known. The AES index accounts for the deviation of the model results from the ensemble mean, hence it provides an indication of the spread of the distribution, i.e., a measure of the confidence in the predicted value. Generally, results of the assimilation are satisfactory when AE and AES of the update ensembles decrease with respect to the corresponding indices of the forecast ensembles. For this reason, in the sequel the relative variation J of these indices is also computed.

3 Test case

3.1 Test case model

The methodology described in Sect. 2 has been carried out for a synthetic test case. The model configuration has been created focusing on an off-shore hydrocarbon reservoir buried in a sedimentary basin with geometries and properties typical of the Northern Adriatic, Italy. The model domain is a parallelepiped with a square basis of about 50 km and depth of about 5 km. It has been subdivided in four layers with different properties: overburden, reservoir, aquifer and underburden. For the sake of simplicity, the first and the last are characterized by a linear elastic constitutive law, in fact their behavior does not significantly affect surface movements (Ferronato et al., 2010; Teatini et al., 2010). A non-linear elasto-plastic constitutive law, namely the modified Cam Clay (De Souza Neto et al., 2008), has been used for the definition of the reservoir and the aquifer behavior. The model domain has been discretized into a 3D finite element mesh composed of 71 734 nodes and 410 030 tetrahedrons. The entire domain has been characterized by a unitary Biot coefficient, a Poisson coefficient equal to 0.30 and a vertical compressibility c_m that follows the law vs. the effective vertical stress σ_z developed by Baù et al. (2002) and Ferronato et al. (2013) for the Northern Adriatic basin, Italy:

$$\begin{array}{rl}& c_m^{\text{I cycle}}=\mathrm{1.0044}\times {\mathrm{10}}^{-\mathrm{2}}\times {\mathit{\sigma }}_z^{-\mathrm{1.1347}}\\ & c_m^{\text{II cycle}}=\mathrm{2.9087}\times {\mathrm{10}}^{-\mathrm{4}}\times {\mathit{\sigma }}_z^{-\mathrm{0.4315}}\end{array}$$

where c_m and σ_z are in [MPa⁻¹] and [MPa], respectively. Homogeneous boundary conditions have been prescribed for displacements, on the lateral and the bottom boundaries, and for stress, on the top surface. As external forces, pore pressure variations have been imposed on the reservoir and aquifer nodes with the aim to simulate a general program of hydrocarbon production with two phases of production separated by a temporary stop from year 3 to year 5 and a final period of natural pressure recovery. Additional details on the geometry and properties of the test case are given in Gazzola et al. (2019).

Since a synthetic test case has been taken into consideration, the geomechanical model has been run both to create the ensembles of Monte Carlo realizations and to define a set of hypothetical measurements. Consequently, a set of statistical distributions and a true configuration of the main geomechanical parameters have to be defined. The modified Cam Clay constitutive law requires the definition of the modified compression index λ^∗, i.e. the slope of the normal consolidation line in the plot of volumetric strain vs. axial stress in natural logarithmic scale, and the modified swelling index k^∗, i.e. the slope of the unloading line (Nguyen et al., 2017). In Spiezia et al. (2017), more details on model properties and implementation have been provided. To simulate a set of GPS recordings (green stars in Fig. 1), the true configuration is selected as follows:

$$\begin{array}{rl}& {\mathit{\lambda }}^{\ast }=\mathrm{0.004992}\\ & k^{\ast }=\mathrm{0.000700}\end{array}$$

In this application, three different cases have been taken into consideration: uncertainties related only to λ^∗, only to k^∗ and to both. The forecast ensembles of vertical displacements u_z (grey lines in Fig. 1) have been generated with the following Gaussian distributions:

$$\begin{array}{rl}& \ln \left({\mathit{\lambda }}^{\ast }\right)\sim \mathcal{N}(-\mathrm{4.9363};\mathrm{0.33295})\\ & \ln \left(k^{\ast }\right)\sim \mathcal{N}(-\mathrm{6.7271};\mathrm{0.50975})\end{array}$$

The covariance matrix of measurement error is required for the application of the DA techniques. It can be computed as the sum of a measurement and an idealisation noise, according to NAM (2017). The first term is an index of the accuracy of the tool for recording the data and the representativeness of the mathematical model for reproducing the observed processes. It has been defined from a normal distribution with zero mean and standard deviation equal to 1.5 mm. The second component takes into consideration the spatial and temporal correlation between measurements. It has been computed following the fractional Brownian motion approach (NAM, 2017) through a fitting process of the variogram of the synthetic observations.

3.2 Model Diagnostic

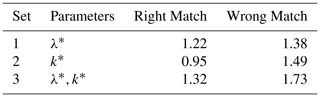
Preliminarily, a model diagnostic procedure, i.e. the χ²-test, has been carried out to evaluate every ensemble through the comparison between the model outcomes and the available measurements. Generally, a χ² value close to one is desirable, while larger values may point out difficulties in constraining the model through the available measurements. Values of χ² smaller than one should be avoided, as they denote a variance associated to the measurements higher than the variance associated to the ensemble. This means that the DA approaches cannot improve the forecast ensemble. Two scenarios have been taken into consideration with the results shown in Table 1. In the first case (third column of Table 1) the state forecast ensembles have been generated with the same constitutive law of the synthetic measurements, i.e. the modified Cam Clay, while in the second case (fourth column) a different constitutive law, i.e. a visco-elasto-plastic one, has been used to create the ensembles. As a matter of fact, in a real study, the constitutive law that describes the behavior of the porous medium is not known a priori. In both scenarios, the χ² value is always close to one, but values of the ensembles generated with the wrong constitutive law are always larger. This suggests that the χ²-test could be effectively used as a tool to select the most suitable constitutive law to describe the porous medium behavior. Only in one case, i.e. when uncertainties are associated to the modified swelling index k^∗, χ² is smaller than one and this could be related to the production program that has been prescribed. As a matter of fact, k^∗ is a parameter that controls the rock behavior in unloading/reloading conditions and consequently does not significantly influence the surface displacements for a hydrocarbon production program.

Table 1 Analyzed configuration sets with their associated uncertain parameters and χ² values for two scenarios: the first one with the right match between the constitutive law that generates the synthetic measurements and the ensembles, and the second one with the wrong match.

Table 2 RF approach: maximum and minimum probabilities of occurrence P for the analyzed ensembles and combination of parameters with maximum P.

3.3 Red Flag

After the model diagnostic, an easy and fast technique for a preliminary analysis of the ensembles is RF. It allows to characterize every realization of the ensemble by its own probability of occurrence. In Table 2 the parameters corresponding to the realization with the largest probability are provided. They are not always the closest set to the true parameters and the reason is twofold. First, the comparison is based on the vertical displacements u_z, that are the effect through the forward model of the parameter selection and not directly the parameters themselves. Second, an error is associated to the observations in order to consider, for example, the accuracy of the measurement tool or possible temporal correlations between successive measurements. Table 2 also provides the maximum and minimum probabilities of occurrence of the analyzed ensembles. They seem to confirm the outcome of the diagnostic stage, in fact for set #1 and #3 the difference between the largest and smallest probability is significant, while for set #2 the maximum probability is smaller and with a similar order of the minimum one.

3.4 Ensemble Smoother

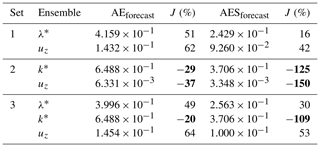
ES has been applied for the three sets of uncertain parameters previously described, with the outcome shown in Fig. 1. They confirm the results obtained by the model diagnostic procedure and the RF technique. In fact, for parameter set #1 results are satisfactory, i.e. the update ensembles of state and parameter are closer to the true values than the forecast ones. Also the positive values of the relative variations J of the update AE and AES with respect to the forecast ones, reported in Table 3, confirm these results. On the contrary, for set #2, results of ES application seem to be not encouraging. As anticipated by the value of χ², the parameter k^∗ does not significantly affect surface movements, i.e. the forecast state ensemble is already quite close to the measurements. This is also shown by the forecast AES values in Table 3. In particular, notice that similar variations of the parameters λ^∗ (AES(${\mathit{\lambda }}^{\ast })=\mathrm{2.429}\times {\mathrm{10}}^{-\mathrm{1}}$ for set #1) and k^∗ (AES($k^{\ast })=\mathrm{3.706}\times {\mathrm{10}}^{-\mathrm{1}}$ for set #2) produce quite different spreads, measured by AES(u_z), of the state ensembles. Consequently, the ES is not effective in constraining the model. Finally, in set #3 the available measurements help to reduce uncertainties both for parameter λ^∗ and for surface measurements similarly to set #1, but not for k^∗.

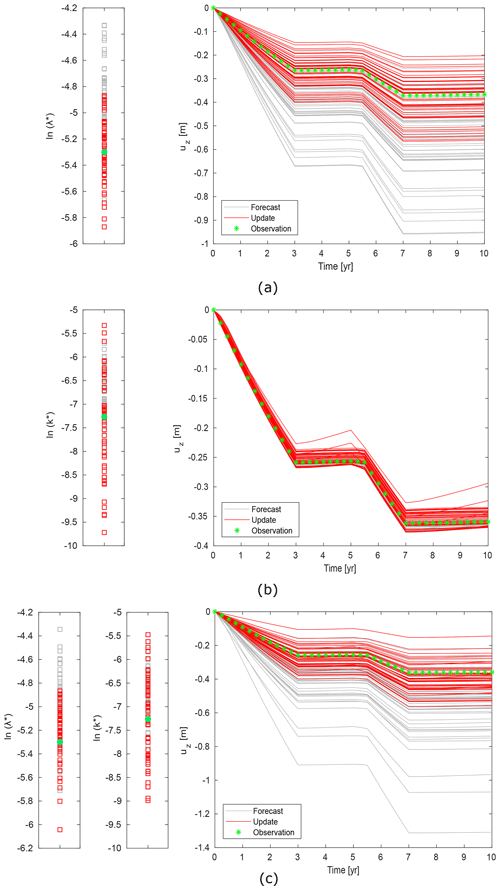
Figure 1 Outcomes of ES for set #1 (a), #2 (b) and #3 (c). Parameters (left panels) and state, i.e. vertical displacements, u_z (right panels), ensembles are shown in grey (forecast) and red (update). Observation data are green stars.

Table 3 ES approach: AE and AES for the forecast ensemble and the relative variation J of AE and AES from the update ensembles. The larger J, the more effective is the assimilation approach on the parameter or state ensembles indicated in column 2. Negative values are highlighted in bold.

ES can be employed also in a predictive sense by assimilating new measurements as they are recorded. Considering set #1, effectiveness of ES improves with the increase of the number of assimilated measurements, but also few observations allow to reduce uncertainties related to parameter and to the state ensembles. Results are shown in Fig. 2 and Table 4.

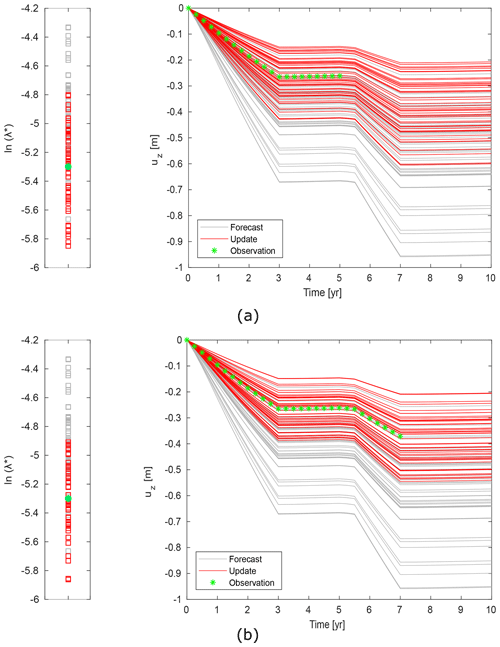
Figure 2 The same as in Fig. 1 for set #1 for the assimilation of 5 years (a) and 7 years (b) of displacements measurements (green stars).

Table 4 Testing ES approach in a predictive sense for set #1. Variations J of AE and AES from the update ensembles assimilating 5, 7 and 10 years of measurements. The AE and AES indices for the forecast ensembles are the same of Table 3. Negative values are highlighted in bold.

4 Conclusions

In this work, a novel methodological approach for a stochastic study of land subsidence due to hydrocarbon exploitation has been developed and tested in a synthetic test case inspired by the Northern Adriatic basin, Italy. The aim is to define an efficient and robust workflow that combines DA techniques and geomechanical models in order to quantify and reduce uncertainties and consequently make the model more accurate and reliable.

First, every ensemble has been evaluated considering the comparison with the available measurements through a model diagnostic procedure, i.e. the χ²-test. An ensemble is considered more appropriate as the associated χ² value is closer to one. From the outcomes of numerical experiments, the χ²-test appears a worthwhile tool to select the most appropriate ensemble for the successive DA techniques, e.g. to define the constitutive law that best approximates the porous medium behavior. After that, RF approach has been used to characterize every Monte Carlo realization by its own probability of occurrence. Despite the parameters of the most probable realization are not always the closest to the true values, RF allows for a preliminary reduction of uncertainties in a fast and cheap way. In fact, if no further analysis is carried out, the least probable realizations can be neglected in the land subsidence study, thus reducing the uncertainty interval. Finally, model state and parameters have been updated through the ES approach. If the forecast ensemble has been properly generated, the ES application to constrain the model through the available measurements proves effective. ES can be used also in a predictive sense, increasing the accuracy of its outcomes while new data are assimilated.

On summary, in the context of a synthetic test case, the proposed workflow seems to be an innovative and suitable approach to study land subsidence above producing hydrocarbon reservoirs, taking into consideration the uncertainties that unavoidably affect numerical models of real world phenomena. Moreover, it allows to reduce these uncertainties in order to obtain more accurate and reliable predictions. Further analyses and improvements on these approaches are currently underway with its application on real-world reservoir problems.