Numerical simulation of land subsidence above an off-shore Adriatic hydrocarbon reservoir, Italy, by Data Assimilation techniques

The numerical prediction of land subsidence above producing reservoirs can be affected by a number of uncertainties, related for instance to the deep rock constitutive behavior, geomechanical properties, boundary and forcing conditions, etc. The quality and the amount of the available observations can help reduce such uncertainties by constraining the numerical model outcome and providing more reliable estimates of the unknown governing parameters. In this work, we address the numerical simulation of land subsidence above a producing hydrocarbon field in the Northern Adriatic, Italy, by integrating the available monitoring data in the computational model with the aid of Data Assimilation strategies. A preliminary model diagnostic analysis, i.e. the χ²-test, allows for identifying the most appropriate forecast ensemble. Then, a Bayesian approach, i.e. the Red Flag technique, and a smoother formulation, i.e. the Ensemble Smoother, provide a significant reduction of the prior uncertainties. The experiment developed on a real-world gas field confirms that the integration of monitoring observations with classical geomechanical models is a valuable approach to improve the reliability of land subsidence predictions and to exploit in a systematic way the increasing amount of available measurement records.

1 Introduction

The numerical prediction of land subsidence above producing reservoirs can be affected by a number of uncertainties, related for instance to the definition of the constitutive law that describes the behavior of the porous medium, geomechanical properties, boundary and forcing conditions, etc. These uncertainties involve in the lack of quality and reliability of the land subsidence prediction. The accuracy and the amount of the available monitoring data, such as surface displacements recorded by GPS stations, can greatly help reduce such uncertainties, by constraining the computational model, solving approximately the inverse problem and providing more reliable estimates of the uncertain governing parameters. A novel efficient workflow that combines Data Assimilation (DA) techniques and geomechanical model has been proposed in a recent work by Gazzola et al. (2019) and improved in Gazzola et al. (2020) with an application to a synthetic test case. The methodology starts from the generation of a set of ensembles of Monte Carlo realizations in order to consider uncertainties associated, for example, to the choice of the constitutive law that describes the porous medium behavior and the values of the geomechanical parameters. Then, the procedure includes a three-steps workflow: (i) a first diagnostic of the ensemble, i.e. the χ²-test, based on the mismatch between the available measurements and the model outcomes, which allows for identifying the most appropriate constitutive law and focusing on one ensemble only; (ii) a Bayesian approach, i.e. the Red Flag (RF) technique, which provides the probability of occurrence of every Monte Carlo realization, and (iii) an ensemble-based DA technique, i.e. the Ensemble Smoother (ES), that updates the model state and parameters, providing a significant reduction of the prior uncertainties on the governing geomechanical parameters, allowing for the quantification and reduction of the expected interval for the predicted ground settlement.

The aim of this methodology is to improve the prediction of land subsidence, avoiding deterministic outcomes that are not realistic. The available measurements train the model in order to improve its accuracy and reliability as new information comes in. This procedure has been applied to a synthetic but realistic test case, resulting in encouraging quantification and reduction of uncertainties (Gazzola et al., 2020).

In this work, we address the numerical simulation of land subsidence above a real-world producing hydrocarbon field in the Northern Adriatic basin, Italy. Available data consist of GPS records for eleven years. A state-of-the-art Finite Element geomechanical model of the multi-pay layered reservoir is implemented, with a one-way coupled approach used to simulate the production program. Three ensembles of the expected land subsidence are generated by using a Modified Cam-Clay (MCC) and a visco-elasto-plastic (VEP) constitutive laws with different set of parameter values.

This methodology provides a significant reduction of the prior uncertainty on the governing geomechanical parameters, which allows to quantify and reduce as well the expected interval for the predicted ground settlement.

The paper is organized as follows. First, a brief description of the methodological approach is provided, then the producing hydrocarbon field and the outcomes of every step of the analyzed workflow are presented and discussed. A final section summarizes the conclusions.

2 Methodological approach

The aim of the methodological approach originally proposed by Gazzola et al. (2019) is to train the numerical model through the available measurements in order to quantify and reduce the uncertainties that unavoidably affect the model outcome.

The starting point of this methodology is to propagate such input uncertainties to the output of the geomechanical model, i.e. the land subsidence prediction, by the generation of a group of forecast ensembles of Monte Carlo realizations that consider, for example, different possible constitutive laws to describe the deep rock behavior and variability ranges for the main mechanical parameters. In fact, at the beginning of a land subsidence study, typically a few pieces of information only are available to characterize the porous medium behavior. Displacement records are collected when the pressure program starts and then used with different DA techniques in order to train the model and make the predictions more accurate and reliable. First, a diagnostic of the ensembles, i.e. the χ²-test, is suggested. This procedure allows for a preliminary validation of the ensemble based on the mismatch between the model outcomes and the available measurements that, for linear problems, follows a χ² distribution with degrees of freedom equal to the number of measurements (Tarantola, 2005). The χ²-test, as already used in Chen and Oliver (2013), Fokker et al. (2016) and Oliver and Alfonzo (2018), provides here an indication of the most suitable ensemble for the successive and more expensive DA steps of the procedure.

The second step of the workflow is the RF approach, as originally proposed by Nepveu et al. (2010). It is a Bayesian approach that combines the likelihood of the measurements with the prior information in order to compute the probability of every realization of the ensemble. This allows for a cheap and fast analysis of the forecast ensemble, since the inverse problem is not solved.

The last step consists in a smoother formulation, i.e. the ES technique. The ES is an ensemble-based technique originally developed by Van Leeuwen and Evensen (1996). It is a non-sequential DA algorithm that updates both model parameters and state variables by combining prior information, measurements, and the solution of the forward model. For the following application, the ES implementation described in Evensen (2003) has been used. When the probability distribution of uncertain parameters is Gaussian, outcomes of ES are optimal (Van Leeuwen and Evensen, 1996). There are many subsidence applications of the ES technique, some recent examples are Baù et al. (2016), Fokker et al. (2016) and Zoccarato et al. (2018). Here, to evaluate the outcomes, one performance index, i.e. the average ensemble spread AES (Hendricks Franssen and Kinzelbach, 2008), and its variation J from the forecast to the update ensemble have been taken into consideration, as in Zoccarato et al. (2016). The AES index defines the spread of the distribution with respect to its mean, hence it identifies the confidence in the predicted values. Generally, when the AES associated to the update ensemble decreases with respect to the corresponding index for the forecast ensemble, i.e. J has a positive value, results of the assimilation are satisfactory.

3 Case study

3.1 The hydrocarbon reservoir geomechanical model

The methodology described in Sect. 2 has been applied to a real reservoir model to evaluate the robustness and efficiency of the proposed approach. An off-shore multi-pay layered hydrocarbon reservoir buried in the Northern Adriatic basin, Italy, has been taken into consideration. The depth of the reservoir is between 2700 and 2850 m below mean sea level. The geomechanical model domain covers an area of about 60 km×66 km and extends down to 7 km below the land surface. The volume has been discretized into a 3D finite element mesh composed of 712 811 nodes and 685 440 hexahedra. Three main constitutive laws have been used to describe the possible behavior of the porous medium: linear-elastic, MCC and VEP. The first one has been associated to the overburden, underburden and sideburden layers because they are not affected by significant stress changes due to the mining activities (Ferronato et al., 2010; Teatini et al., 2010). To generate the ensembles, the aquifer and the reservoir have been characterized by two different non-linear models, that are both representative of the possible behavior of a deep porous volume subject to pressure variations (Spiezia et al., 2017; Isotton et al., 2019). In particular, an elasto-plastic rate-independent model, namely the MCC (De Souza Neto et al., 2008), and a VEP rate-dependent based on Vermeer-Neher theory (Vermeer and Neher, 1999) have been used. A unitary Biot coefficient and a Poisson coefficient equal to 0.30 have been prescribed for the entire domain, while the vertical compressibility c_m changes with the effective vertical stress σ_z, following the law developed by Baù et al. (2002) and Ferronato et al. (2013) for the Northern Adriatic basin, Italy:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{c}_m^{\text{I cycle}}=\mathrm{1.0044}\times {\mathrm{10}}^{-\mathrm{2}}\cdot {\mathit{\sigma }}_z^{-\mathrm{1.1347}}\\ {\displaystyle }& {\displaystyle }{c}_m^{\text{II cycle}}=\mathrm{2.9087}\times {\mathrm{10}}^{-\mathrm{4}}\cdot {\mathit{\sigma }}_z^{-\mathrm{0.4315}}\end{array}$$

where c_m and σ_z are in [MPa⁻¹] and [MPa], respectively.

Land subsidence has been predicted through a one-way coupled approach with the pore pressure values in time and space considered as a deterministic sources of strength and imposed on the reservoir and aquifer nodes. In fact, uncertainties on the flow field are negligible if compared with those on mechanical parameters due to the large amount of available information for the history matching of the reservoir model. Moreover, for the time and scales of interest, this simplified approach is generally acceptable (Gambolati et al., 2000) and particularly justified for gas reservoirs, where the coupling effects are usually weak.

The numerical simulations last for 40 years, including a first production period of about 7 years followed by a 4-years recovery step before the forecast phase of about 29 years.

On the lateral and the bottom boundaries, homogeneous boundary conditions have been prescribed, while the top of the domain, which represents the land surface, is modeled as a traction-free boundary.

3.2 Ensemble Generation and Model Diagnostic

The generation of the ensembles has been done by running the geomechanical model with a set of statistical distributions of the input parameters. Three ensembles, each composed of 50 realizations, have been created by using the MCC and the VEP constitutive laws with different set of parameter values. In particular, we consider uncertain the modified compression index λ^*, i.e. the slope of the normal consolidation line in the plot of volumetric strain vs axial stress in natural logarithmic scale (Nguyen et al., 2017). The methodological approach used in the present work is actually conceived for the characterization of more than one uncertain geomechanical parameter. Here, for the sake of simplicity, we focus the analysis on one parameter only, which appears to be the most significant parameter for a hydrocarbon production program (Gazzola et al., 2019). For more details on the application of this approach for more than one uncertain parameter, see Gazzola et al. (2020).

The first two ensembles of vertical displacements u_z have been obtained by using the following Gaussian distribution of λ^*:

$$\ln \left({\mathit{\lambda }}^{*}\right)\sim \mathcal{N}(\mathit{\mu };\mathit{\varsigma })$$

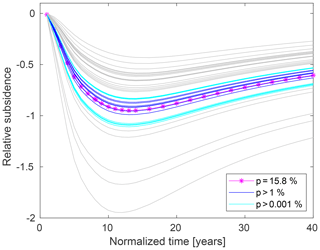
with mean μ equal to −4.3450 and standard deviation ς equal to 0.6659. These parameters are chosen according to the variability range of c_m typical of the Northern Adriatic basin, Italy, for a 95 % confidence interval (Baù et al., 2002), for both the MCC and VEP constitutive laws. The resulting forecast ensembles are shown in Fig. 1. Grey lines in Figs. 1 and 3 refer to the relative subsidence values in time normalized with respect to the last GPS record available.

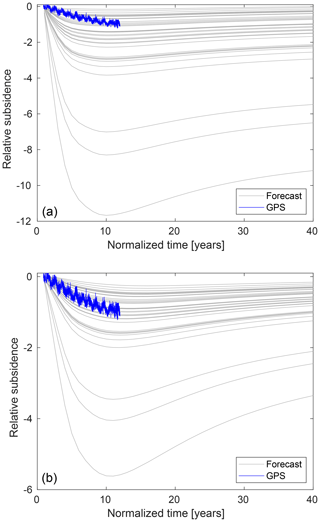
Figure 1 Forecast state ensemble (grey lines), i.e. relative vertical displacements u_z in time, for the MCC (a) and the VEP (b) behavior and available relative GPS records (blue line). The actual displacements are normalized with respect to the last GPS record available. The associated probability distributions and χ² values are provided in the first two rows of Table 1.

To train the model, a set of displacement measurements recorded by a GPS station is available. In particular, the GPS measurements recorded at the times when pressure records are available are used for the assimilation.

For the application of the DA techniques, the covariance matrix of measurement error has to be computed. We consider a diagonal matrix with a standard deviation equal to 5 mm that accounts for the accuracy of both the GPS station and the mathematical model used to reproduce the observed processes.

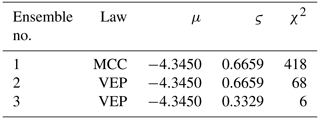
First, a diagnostic of the forecast ensembles has been carried out. The outcome of the χ²-test is shown in Table 1, where the values are computed as a mean of the χ² of every realization of the ensemble and then scaled by the number of measurements. Generally, the better is an ensemble, the closer to one is the relative χ² value. Despite of this, values of χ² smaller than one should be avoided because they denote a variance associated to the measurements larger than the ensemble variance and consequently the DA approaches cannot improve the forecast ensemble. The ensembles generated with the previous probability distribution present large χ². The time behavior of the relative u_z computed with the forward model and the MCC constitutive law (Fig. 1a) has a trend significantly different from that characterizing the measurements. The VEP ensemble (Fig. 1b) appears to better fit the behavior of the GPS records, but its χ² value is also large. Consequently, a third ensemble has been created, considering the VEP constitutive law and the 68 % confidence interval for c_m according to Baù et al. (2002). As a result of the χ²-test, this ensemble (Table 1) seems more representative of the measured data and consequently only this ensemble has been used for the successive DA applications (Figs. 2 and 3).

Table 1 Analyzed ensembles with their associated constitutive laws, parameters (μ and ς) of the probability distribution of λ^* and χ² values.

3.3 Red Flag

After the model diagnostic, RF is an easy and fast technique to analyze the ensemble by characterizing every realization by its own probability of occurrence. The outcomes of RF are shown in Fig. 2, where the forecast ensemble is colored considering different ranges of probabilities. The minimum probability of occurrence of the analyzed ensemble is almost null, while the maximum (associated to the pink realization of Fig. 2) is 15.80 %. The variability range of the probabilities of the ensemble is very large, thus confirming the results of the χ²-test, similarly to the synthetic analyses in Gazzola et al. (2020), and points out that this ensemble is suitable for the application of ES.

RF technique could be used also for a preliminary reduction of the uncertainties that affect the ensemble, by neglecting the realizations characterized by the smallest probability of occurrence that are, for example, grey lines in Fig. 2. As a matter of fact, RF has a tendency to ensemble collapse when many data points are present. As a consequence, this approach should be properly used only for a first screening of the ensemble.

Figure 2 Outcomes of RF for the forecast state ensemble, the third in Table 1. Every realization is colored depending on its probability of occurrence p.

3.4 Ensemble Smoother

The ES technique allows to update both parameter and state variables. The outcomes are shown in Fig. 3, where the update ensemble (red lines) is obtained by running the forward model with the update ensemble of the parameter λ^*. These results agree with those obtained by the model diagnostic procedure and the RF approach. In fact, the application of ES provides a reduction of the uncertainties that affect the model, constraining it to the available measurements. The variation J of the AES index is equal to 50 % and 38 % for the parameter and state ensemble, respectively, i.e. the spread of the ensemble around its mean decreases.

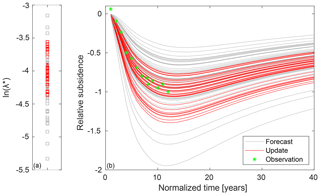
Figure 3 Parameter (a) and state (b) ensembles resulting from the ES application. The forecast and update ensembles are grey and red, respectively, while the observation data are the green stars.

The ES can be a useful tool also in a predictive sense by assimilating new measurements as they are recorded. To evaluate this capability, measurements have been assimilated by increasing steps of about 2 years. The outcomes are shown in Fig. 4 for the parameter ensemble and in Table 2 for both parameter and state variables. In this case, the update state ensembles used to compute J in Table 2 derive directly as an outcome of the ES approach and are not computed by running the forward model with the updated parameter sets.

Table 2 Testing ES approach in a predictive sense. Variations J of AES index for the parameter λ^* and the state u_z for the assimilation of increasing amount of GPS recordings.

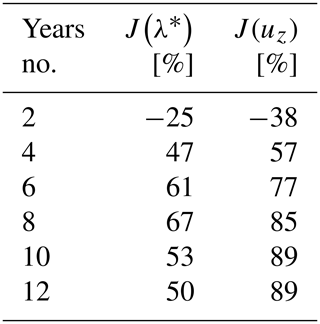
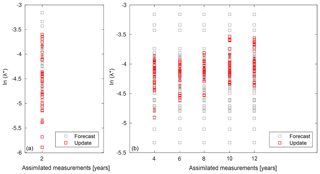
Figure 4 Outcomes of ES used in a predictive sense: parameter ensembles for increasing years of assimilated measurements.

Except for the assimilation of only 2 years of measurements, there is always a reduction of uncertainties for both parameter and state variables. The variation J(λ^*) increases until 8 years, but the assimilation slightly worsens when 10 and 12 years are accounted for. Despite of this, the index AES(u_z) gradually decreases, i.e. J(u_z) increases, pointing out a progressive abatement of the uncertainties and a better fitting of the measurements.

4 Conclusions

In this work, the novel methodological approach developed by Gazzola et al. (2020) for a stochastic study of land subsidence caused by hydrocarbon exploitation has been tested in a real-world case with the aim at evaluating its capability and robustness. The analyzed workflow combines the geomechanical model with DA techniques in order to account for uncertainties that affect any study of a real-world process and consequently to avoid deterministic outcomes that could not be matched by measurements recorded during the reservoir production life after the release of the geomechanical modeling outcomes. This procedure allows to achieve more accurate and reliable results by training the numerical model with the available measurements. Here, this methodology has been tested for an off-shore hydrocarbon reservoir buried in the Northern Adriatic basin, Italy, subject to a production program and monitored by a GPS station.

First, three ensembles have been generated by considering two non-linear constitutive laws, i.e. the MCC and the VEP behavior, and two different confidence intervals to describe the main mechanical parameter λ^*.

A model diagnostic procedure carried out by the χ²-test allows to choose the most appropriate ensemble for the successive DA approaches through the comparison between the model outcomes and the available measurements.

After the diagnostic of the ensemble, every Monte Carlo realization has been characterized by its own probability of occurrence through the RF technique. This approach could be used for a preliminary reduction of the uncertainties that affect the model by neglecting the least probable realizations of the forecast ensemble.

Finally, the ES technique has been used to reduce the uncertainties without neglecting any realization, by updating the state and parameter ensembles. The model has been trained by the available measurements, resulting in an effective reduction of the uncertainties and in a more reliable subsidence prediction. The ES could be used also in a predictive sense by assimilating new observations as they become available. Adding new measurements seems to result in a more effective constraining of the model, but also a relative few years of assimilated observations appear to be enough for a first reduction of uncertainties in this case study.

On summary, the application of the proposed methodology for a real-world hydrocarbon reservoir confirms the results obtained for the synthetic test case. This workflow allows for (i) a stochastic study of land subsidence; (ii) a reduction of the uncertainties that affect the numerical model and (iii) more accurate and reliable land subsidence predictions. The approach here presented represents a way to investigate land subsidence different from the traditional methodologies. The traditional (or “deterministic”) procedures generally use the available measurements to calibrate the geomechanical model in order to define the set of parameters that allows the optimal reproduction of the observations. In this way, there could be the need to re-calibrate the model as new information become available, i.e. update the values of the geomechanical parameters. Conversely, the proposed workflow starts the geomechanical study at the very beginning of the reservoir life combining uncertainties to the numerical model by the creation of an ensemble of realization. Then, when measurements become available, such uncertainties are reduced, with the reduction depending on the observation accuracy, but not eliminated in order to avoid the ensemble collapse and keep open the possibility to stochastically reproduce further records. This approach allows to take advantages from the available measurements, in fact they are not used only to monitor the evolution of land subsidence in time, but also to train the geomechanical model.