Multi‐scale simulation of rock compaction through breakage models with microstructure evolution

Regional subsidence due to fluid depletion includes the interaction among multiple physical processes. Specifically, rock compaction is governed by coupled hydro-mechanical feedbacks involving fluid flow, effective stress change and pore collapse. Although poroelastic models are often used to explain the delay between depletion and subsidence, recent evidence indicates that inelastic effects could alter the rock microstructure, thus exacerbating coupling effects. Here, a constitutive law built within the framework of Breakage Mechanics is proposed to account for the inherent connection between rock microstructure, hydraulic conductivity, and pore compaction. Furthermore, it is embedded into a 1-D hydromechanical coupled finite element analysis (FEA) to explore the effects of micro-structure rearrangement on the development of reservoir compaction. Numerical examples with the proposed model are compared with simulations under constant hydraulic conductivity to illustrate the model capability to capture the non-linear processes of reservoir compaction induced by fluid depletion.

1 Introduction

Various anthropogenic activities are responsible for the occurrence of surface subsidence and damage to buildings and infrastructure. Among these, rock compaction and land subsidence are major concerns in hydrocarbon reservoirs (Zoback, 2010). Reservoir depletion lowers the fluid pressure, leads to an increase in the stress carried by the rock skeleton, and generates non-negligible compaction. Diagnostic tools are necessary to understand and forecast regional subsidence, but a challenging obstacle in such analyses is the interaction of multiple physical processes operating over a wide range of time and length scales. Poroelastic modeling frameworks are often used to compute either near-field reservoir compaction or far-field subsidence (Du and Olson, 2001). However, poroelastic models restrict the analysis to linear deformation processes, thus ruling out possible inelastic changes in rock microstructure (i.e., particle crushing, particle rearrangement, and pore collapse) caused by compaction and the consequent hydro-mechanical couplings deriving from them (Esna Ashari et al., 2018). In this circumstance, more advanced constitutive laws are needed to capture the material properties and connect the particle-scale processes to macro-scale fluid flow characteristics. For this purpose, a new constitutive relationship within the framework of Breakage Mechanics is developed and the particular case of the Groningen gas field (Roels, 2001; Hol et al., 2015; van Thienen-Visser and Fokker, 2017) is used to validate the proposed model. Different modeling scenarios (e.g., elastic and inelastic compaction, constant hydraulic conductivity, and concurrent change of compressibility and hydraulic conductivity) are simulated to illustrate the potential impact of inelastic processes on reservoir compaction.

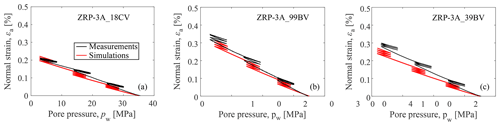
Figure 1 Simulations of the UPPD/M tests with two end-member porosities (test ID: ZRP-3A_18CV and ZRP-3A_39BV) and the medium porosity (test ID ZRP-3A_99BV).

Table 1 Summary of model parameters typical in the Groningen gas field.

2 Constitutive modeling

2.1 Partially coupled breakage model

Breakage mechanics is a constitutive framework built within the frame of continuum thermodynamics to study the inelastic deformation of granular solids subjected to changes in grain size distribution due to particle crushing. Such approach requires the definition of a Helmholtz free energy Ψ, which in case of linear elasticity can be expressed as:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\mathrm{\Psi }& =\left(\mathrm{1}-\mathit{\theta }B\right)[{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}K{\left({\mathit{\epsilon }}_{\mathrm{v}}^{\mathrm{e}}\right)}^{\mathrm{2}}+{\displaystyle \frac{\mathrm{3}}{\mathrm{2}}}G{\left({\mathit{\epsilon }}_{\mathrm{q}}^{\mathrm{e}}\right)}^{\mathrm{2}}],\\ \mathit{\theta }& =\mathrm{1}-{\displaystyle \frac{{\int }_{d_{\mathrm{m}}}^{d_{\mathrm{M}}}{p}_{\mathrm{u}}\left(x\right)x^{\mathrm{2}}\mathrm{d}x}{{\int }_{d_{\mathrm{m}}}^{d_{\mathrm{M}}}{p}_{\mathrm{0}}\left(x\right)x^{\mathrm{2}}\mathrm{d}x}}\end{array}\end{array}$$

where ${\mathit{\epsilon }}_{\mathrm{v}}^{\mathrm{e}}$ and ${\mathit{\epsilon }}_{\mathrm{q}}^{\mathrm{e}}$ are the volumetric and deviatoric elastic strain; B is the breakage index; K and G are the elastic bulk and shear modulus; d_m and d_M are the minimum and maximum particle diameters; θ is a grading index associated with the initial and ultimate grain size distribution (GSD), p₀(d) and p_u(d) (Einav, 2007a). Here, a Pearson distribution is used to describe mathematically the grading characteristics of a granular rock, eventually using experimental data to constrain the model parameters (Hol et al., 2018).

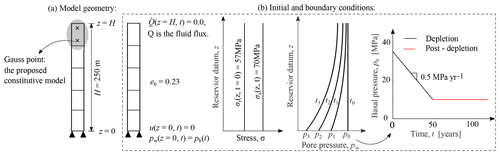
Figure 2 Schematic description of model setup: (a) model geometry; (b) initial and boundary conditions.

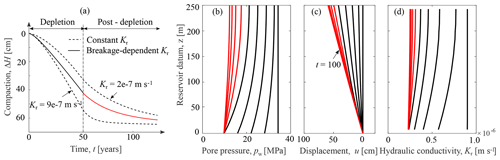
Figure 3 Simulations of a single reservoir compaction during and after depletion: (a) time history of reservoir compaction; (b, c) 25-year isocrones of the nodal pore pressure and displacement; (d) 25-year isocrones of hydraulic conductivity at gauss points.

Generally, brittle granular materials present two coupled dissipative mechanisms: plasticity and breakage. This work simply assumes that coupling exists only in compression, while the shear response is solely governed by frictional plasticity:

$$\begin{array}{}\text{(2)}& \mathit{\delta }\mathrm{\Phi }=\sqrt{{\left(\mathit{\delta }{{\mathrm{\Phi }}_{\mathrm{v}}^{\mathrm{p}}}^{*}\right)}^{\mathrm{2}}+{\left(\mathit{\delta }{\mathrm{\Phi }}_{\mathrm{B}}^{*}\right)}^{\mathrm{2}}}+\mathit{\delta }{\mathrm{\Phi }}_{\mathrm{q}}^{\mathrm{p}}\end{array}$$

in which the individual terms are being factorized as $\mathit{\delta }{{\mathrm{\Phi }}_{\mathrm{v}}^{\mathrm{p}}}^{*}={\sin }^{-\mathrm{1}}\left(\mathit{\omega }\right)\mathit{\delta }{\mathrm{\Phi }}_{\mathrm{v}}^{\mathrm{p}}$ and $\mathit{\delta }{\mathrm{\Phi }}_{\mathrm{B}}^{*}={\cos }^{-\mathrm{1}}\left(\mathit{\delta }{\mathrm{\Phi }}_{\mathrm{B}}\right)$ (Einav, 2007b), and:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& \mathit{\delta }{\mathrm{\Phi }}_{\mathrm{v}}^{\mathrm{p}}=p{\displaystyle \frac{E_{\mathrm{c}}}{E_{\mathrm{B}}{\left(\mathrm{1}-B\right)}^{\mathrm{2}}}}\mathit{\delta }{\mathit{\epsilon }}_{\mathrm{v}}^{\mathrm{p}},\mathit{\delta }{\mathrm{\Phi }}_{\mathrm{q}}^{\mathrm{p}}=\left(M_{\mathrm{f}}p+q_{\mathrm{0}}\right)\mathit{\delta }{\mathit{\epsilon }}_{\mathrm{q}}^{\mathrm{p}},\\ & \mathit{\delta }{\mathrm{\Phi }}_{\mathrm{B}}={\displaystyle \frac{E_{\mathrm{c}}}{{\left(\mathrm{1}-B\right)}^{\mathrm{2}}}}\mathit{\delta }B\end{array}\end{array}$$

where E_B is the breakage energy. E_c is the critical breakage energy. p and q are the mean effective stress and deviatoric stress. ${\mathit{\epsilon }}_{\mathrm{v}}^{\mathrm{p}}$ and ${\mathit{\epsilon }}_{\mathrm{q}}^{\mathrm{p}}$ are the volumetric and deviatoric plastic strain. $M_{\mathrm{f}}=\mathrm{6}\sin \mathit{\varphi }/\left(\mathrm{3}-\sin \mathit{\varphi }\right)$, $q_{\mathrm{0}}=\mathrm{6}c\cos \mathit{\varphi }/\left(\mathrm{3}-\sin \mathit{\varphi }\right)$. c is the cohesive shear strength and ϕ is the effective friction angle. It leads to two separate yielding criteria, the compressive breakage criterion f_B and the frictional shear failure f_f, here expressed as (Einav, 2007a, b):

$$\begin{array}{}\text{(4)}& f_{\mathrm{B}}={\displaystyle \frac{E_{\mathrm{B}}{\left(\mathrm{1}-B\right)}^{\mathrm{2}}}{E_{\mathrm{c}}}}-\mathrm{1}\le \mathrm{0},f_{\mathrm{f}}={\displaystyle \frac{q}{M_{\mathrm{f}}p+q_{\mathrm{0}}}}-\mathrm{1}\le \mathrm{0}\end{array}$$

and it obeys the following flow rules (Das et al., 2011):

$$\begin{array}{}\text{(5)}& \begin{array}{rl}& \text{d}{\mathit{\epsilon }}_{\mathrm{v}}^{\mathrm{p}}=\mathrm{2}{\mathrm{\Lambda }}_{\mathrm{B}}{\displaystyle \frac{E_{\mathrm{B}}{\left(\mathrm{1}-B\right)}^{\mathrm{2}}}{p{E}_{\mathrm{c}}}}{\sin }^{\mathrm{2}}\mathit{\omega },\text{d}{\mathit{\epsilon }}_{\mathrm{q}}^{\mathrm{p}}={\mathrm{\Lambda }}_{\mathrm{f}}{\displaystyle \frac{\mathrm{1}}{M_{\mathrm{f}}p+q_{\mathrm{0}}}},\\ & \text{d}B=\mathrm{2}{\mathrm{\Lambda }}_{\mathrm{B}}{\displaystyle \frac{{\left(\mathrm{1}-B\right)}^{\mathrm{2}}}{E_{\mathrm{c}}}}{\cos }^{\mathrm{2}}\mathit{\omega }\end{array}\end{array}$$

where Λ_B and Λ_f are non-negative plastic multipliers.

2.2 Simulation of cyclic depletion-inflation paths

Standard plasticity models are usually unable to replicate plastic strains prior to the intersection of a yield surface and neglect any inelastic deformation caused by loading-unloading cycles taking place in the pre-yielding regime. However, ample evidence has proved that plastic strains start to accumulate much earlier than the classic yielding cap (van Thienen-Visser and Fokker, 2017; Pijnenburg et al., 2018; Hol et al., 2018). To circumevent this limitation, hypo-plastic modeling techniques can be incorporated (Einav, 2012). This choice implies the use of flow rules adjusted through multiplicative coefficients taking into account the distance of current stress state from the yield surface:

$$\begin{array}{}\text{(6)}& \begin{array}{rl}& \text{d}{{\mathit{\epsilon }}_{\mathrm{v}}^{\mathrm{p}}}^{*}={\left(f_{\mathrm{B}}+\mathrm{1}\right)}^{s_{\mathrm{B}}}\text{d}{\mathit{\epsilon }}_{\mathrm{v}}^{\mathrm{p}},\text{d}{{\mathit{\epsilon }}_{\mathrm{q}}^{\mathrm{p}}}^{*}={\left(f_{\mathrm{f}}+\mathrm{1}\right)}^{s_{\mathrm{f}}}\text{d}{\mathit{\epsilon }}_{\mathrm{q}}^{\mathrm{p}},\\ & \text{d}{B}^{*}={\left(f_{\mathrm{B}}+\mathrm{1}\right)}^{s_{\mathrm{B}}}\text{d}B\end{array}\end{array}$$

where s_B and s_f are the hypo-plastic model parameters for breakage mechanics and frictional plasticity, respectively.

2.3 Breakage permeability variation

Microfracturing (i.e., particle crushing and cement damage) can have a dominant role on the diffusive processes responsible for macroscopic rock permeability (Zhang and Buscarnera, 2018). Here, the approach suggested by Esna Ashari et al. (2018) is followed to model permeability changes due to inelastic compaction. Specifically, an augmented breakage-dependent Kozeny equation is used:

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{\displaystyle \frac{k}{k_{\mathrm{0}}}}& ={\displaystyle \frac{K_{\mathrm{r}}}{K_{\mathrm{0}}}}={\left({\displaystyle \frac{n}{n_{\mathrm{0}}}}\right)}^{\mathrm{3}}{\left({\displaystyle \frac{D_{\mathrm{H}}}{D_{\mathrm{H}\mathrm{0}}}}\right)}^{\mathrm{2}},\\ {\displaystyle \frac{\mathrm{1}}{D_{\mathrm{H}}}}& =\left(\mathrm{1}-B\right){\displaystyle \frac{\mathrm{1}}{D_{\mathrm{H}\mathrm{0}}}}+B{\displaystyle \frac{\mathrm{1}}{D_{\mathrm{Hu}}}}\end{array}\end{array}$$

where n and n₀ are the current and initial porosity; k and k₀ are the current and initial permeability; K_r and K₀ are the current and initial hydraulic conductivity resulting from $K_{\mathrm{r}}={\mathit{\rho }}_{\mathrm{f}}gk/{\mathit{\mu }}_{\mathrm{f}}$, where ρ_f and μ_f are the density and viscosity of reservoir fluid, and g is the gravitational acceleration; D_H is the current harmonic mean grain size, with D_H0 and D_Hu being the values of D_H corresponding to the initial and ultimate GSD:

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{\mathrm{1}}{D_{\mathrm{H}\mathrm{0}}}}=\underset{d_{\mathrm{m}}}{\overset{d_{\mathrm{M}}}{\int }}{p}_{\mathrm{0}}\left(x\right){\displaystyle \frac{\mathrm{1}}{x}}\text{d}x,{\displaystyle \frac{\mathrm{1}}{D_{\mathrm{Hu}}}}=\underset{d_{\mathrm{m}}}{\overset{d_{\mathrm{M}}}{\int }}{p}_{\mathrm{u}}\left(x\right){\displaystyle \frac{\mathrm{1}}{x}}\text{d}x\end{array}$$

3 Example of application to the Groningen gas field

3.1 Model performance

In this work, data relative to the Groningen gas field were used to validate the model performance (Roels, 2001). The UPPD/M tests (multicycle Uniaxial-strain Pore Pressure Depletion tests) reported by Hol et al. (2018) are used to calibrate the model parameters. The UPPD/M samples were subjected to three depletion stages (Stage #1: p_w decreases from 35 to 25 MPa, Stage #2: from 25 to 15 MPa, and Stage #3: from 15 to 1 MPa). Each of the stage was followed by 3 unloading-reloading cycles during which the magnitude of the variation in p_w was 5 MPa. The model formulation described in the preceding sections postulates elastic behavior during unloading and accumulation of permanent (plastic) strain during loading cycles. Measurements available for the different loading/unloading cycles were used to constrain the model parameters summarized in Table 1. Figure 1 shows the model performance for the UPPD/M tests characterized by different values of porosity. Despite some differences between measurements and simulations, the model generally displays a satisfactory performance for all the considered cases.

3.2 Simulation of reservoir compaction

To numerically investigate the effects of material non-linearity on the development of reservoir compaction, the calibrated model is embedded into a 1-D coupled hydro-mechanical finite element (FE) solver (Sloan and Abbo, 1999). As schematically described in Fig. 2, a reservoir column with thickness of 250 m is subjected to a prescribed basal depletion p_b. Figure 2b illustrates the initial and boundary conditions of the simulated reservoir. As shown, it involves the fixed axial stress equal to 70 MPa and the initial radial stress equal to 57 MPa, which is typical across the Groningen gas field. Based on the reported field history, the basal depletion is imposed with an initial pore pressure of 35 MPa and a depletion rate of 0.5 MPa yr⁻¹. Figure 3a compares the predicted time history of reservoir compaction obtained with a breakage dependent hydraulic conductivity to those obtained under constant hydraulic conductivity. The two end-member values of hydraulic conductivity (i.e., $K_{\mathrm{r}}=\mathrm{2.0}\times {\mathrm{10}}^{-\mathrm{7}}$ and $K_{\mathrm{r}}=\mathrm{9.0}\times {\mathrm{10}}^{-\mathrm{7}}$ m s⁻¹) in Fig. 3d are selected for comparison. Figure 3b–d plots the 25-year isochrones of pore pressure, displacement, and hydraulic conductivity during and after basal depletion for the proposed model. The simulations readily show that microstructural changes due to particle crushing exacerbate hydro-mechanical couplings by lowering the hydraulic conductivity. As a consequence, fluid flow proceeds at a lower rate and the development of reservoir deformation is delayed. As shown in Fig. 3a, the compaction response with the evolving K_r is initially close to the behavior of constant high K_r, but as the occurrence of breakage, it tends to approach the response obtained for the lowest (constant) value of K_r.

4 Conclusion and discussion

Microstructure evolution caused by stress changes is a major cause of the inelastic deformation and hydro-mechanical coupling. In this paper, a constitutive law has been developed within the framework of Breakage Mechanics to link the micro-scale and the macro-scale response of a compacting rock, as well as to estimate the permeability variations caused by breakage. A 1-D hydromechanical coupled FE solver has been implemented to explore the impacts of microstructure evolution on reservoir compaction. Data relative to the Groningen gas field have been used to illustrate the model characteristics and test its performance. The model has been calibrated and validated with reference to data for rock cores subjected to the UPPD/M testing protocol. Finally, numerical simulations characterized by both constant and breakage-dependent hydraulic conductivity have been conducted to emphasize the non-negligible impact of inelastic effects. Such analyses show that inelastic processes at the grain-scale can significantly decelerate the pore pressure diffusive process, eventually manifesting as additional sources of delayed reservoir compaction. The geomechanical models discussed in this paper can be a springboard for further studies addressing the challenging problem of simulating field-scale ground subsidence triggering by compaction, for example by integrating near-field simulations with analytical solutions (Geertsma, 1973; Mehrabian and Abousleiman, 2015) or numerical modeling platforms (Lewis et al., 2003).