Atlantis, a tool for producing national predictive land subsidence maps of the Netherlands

A tool is presented that allows efficient and largely automated production of predictive land subsidence maps on a national scale in the Netherlands. The tool, based on Python scripts, is named Atlantis and calculates the subsidence induced by phreatic groundwater level management in Holocene soft-soil areas through peat oxidation and consolidation. Process formulation, input datasets and data handling procedures are elucidated. Maps produced with Atlantis will soon be available online.

1 Introduction

A large part of the coastal zone of the Netherlands subsides at rates that typically range from 0–10 mm yr⁻¹. Although the rates are relatively low, in the course of decades, the subsidence has important consequences for urban and rural water management, infrastructure, and land-use in general. Adaptation to land subsidence, generally by further lowering of the surface water levels to lower phreatic ground water levels, has occurred relatively unconsciously for about a millennium already (e.g. Erkens et al., 2016). Over the last few decades, awareness of subsidence and its impacts has grown with government bodies and has started to become integrated in policy making. That is, adaptation to land subsidence is progressively being addressed more consciously and in a proactive manner.

Since about 1997 (report Werkgroep klimaatverandering en bodemdaling, 1997) efforts have been undertaken to support and facilitate the policy process by producing nationwide predictive land subsidence maps that indicate how subsidence may progress a few decades into the future or longer. These maps were generally spreadsheet-based, with the applied methods poorly documented, and calculation times were largely prohibitive (months for a single map). A major step was adding the possibility of executing the calculation in a GIS environment. The resulting software, named Phoenix (Van der Schans and Houhuessen, 2011), is for instance used in the national cost-benefit analyses on land subsidence in the Netherlands (Van den Born et al., 2016). However, this model was not open source, and still difficult to update and expand when new knowledge would be available. Therefore, new efforts were therefore recently undertaken to develop a new software environment, dubbed Atlantis, that by using modern techniques overcome these limitations, thereby allowing for efficient and largely automated production of predictive land subsidence maps on a national scale and covering time periods of a few decades to centuries.

Atlantis integrates and generalizes calculation methods that were previously conducted in spreadsheets and GIS applications. Atlantis does not only allow prediction of subsidence under business-as-usual but is specifically meant to allow exploration of the impact of policy options and climate change impacts. Published maps can be efficiently updated when changes occur in underlying datasets, and new subsidence components, datasets or process formulations can be readily accommodated within the modular structure of the code.

2 Processes and voxel approach

2.1 Groundwater level management cycle

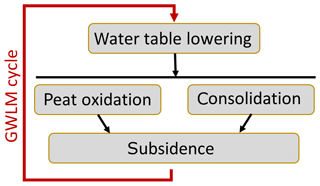
Presently, Atlantis focuses on projections of subsidence caused by phreatic groundwater level management (GWLM) (Fig. 1). GWLM-driven subsidence has been initiated in the distant past by construction of canals, ditches and drains to create arable land. This caused shrinkage of the soils, and oxidation of peat above the lower groundwater level and consolidation and compaction of underlying saturated Holocene deposits (e.g. Erkens et al., 2016). The subsidence gradually decreases the thickness of the unsaturated zone. To re-establish the unsaturated zone thickness required for the local land-use, the surface water level and drainage levels are periodically lowered to compensate for the subsidence, which initiates a new cycle of subsidence (Fig. 1). In areas with thick peat layers, this process can continue for many centuries and cause subsidence of several meters (Erkens et al., 2016).

Figure 1 Schematic representation of the groundwater management cycle.

2.2 Discretization, data requirements and load steps

The total model area of the Netherlands is discretized by a grid of rectangular cells. Cells are grouped into contiguous zones or blocks that represent water level management areas (WLMA) (Fig. 2a). WMLA's are parts of a water board district in which a single surface water level is maintained. The spatial variation of subsidence within these blocks is mainly steered by the distribution, depth and thickness of oxidation- and consolidation susceptible layers within the Holocene deposits, and by the groundwater level. To capture these conditions, Atlantis interfaces with external national and regional dataset of the present land surface elevation, the phreatic groundwater level and the geology. Calculations are carried out for individual columns that consist of a stack of 3-dimensional cells (voxels) (Fig. 2). The voxels are assigned a lithology and parameter values required for the oxidation and consolidation calculations. The basic voxel model is adopted from the national geological model GeoTOP (Stafleu et al., 2012). GeoTOP presently includes a resolution of 100 m × 100 m × 0.5 to 50 m below Dutch ordinance level. The basic model can be refined with regional data sets that include higher resolution data in the vertical.

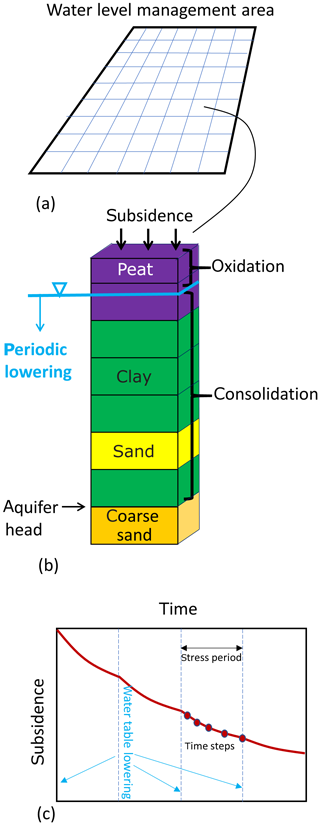
Figure 2 Different component of discretization. (a) The total model domain is subdivided into cells that are grouped into WLMA's (generally not rectangular). (b) Schematic representation of a voxel stack for an individual cell. (c) Time discretization in terms of stress periods and time steps.

Following MODFLOW (McDonald and Harbaugh, 1988) terminology, the time dimension is categorized in terms of stress periods and timesteps (Fig. 2c). A stress period is the time during which a constant stress is applied (for example the surface water stage in a management area or a surcharge). Within a stress period, time is discretized into individual timesteps. A stress period therefore generally consists of multiple timesteps, and a simulation may consist of multiple stress periods. These may all vary in duration.

In each time step both a consolidation and oxidation calculation are performed, and associated height loss of each voxel due to either process is stored. The total land surface subsidence that occurred in a stress period is used to quantify the water table lowering that is applied at the start of the next stress period. The lowering can be set equal to the average or median subsidence in the WLMA the model cell of (Fig. 1a), or equal to the subsidence of the individual cell. To accommodate both oxidation and consolidation with a single water table measure, the water table is considered to represent the mean (long-term) low water table (MLWT: Dutch: GLG) that is widely used in water management practice in the Netherlands.

2.3 Consolidation

2.3.1 Compression models

Presently, two compression models have been implemented to quantify consolidation; the Koppejan model and the isotache model. The Koppejan (Terzaghi-Buisman) model (1948) has been the classical Dutch compression model for settlement calculations for many years (CUR, 1996). The advantage of this model is that it is widely known among geotechnical engineers. The main limitation is the lack of a rate-based formulation, which complicates use with multiple loading events (e.g. in Atlantis long-term effects due to prior stress periods are neglected when using the Koppejan method), and which does not allow the initial condition to include a subsidence rate due to creep. Therefore, also a more advanced model can be chosen.

The isotache model (Den Haan, 1996; Kooi et al., 2018) has become the recommended model for settlement modelling in the Netherlands since about one decade. It overcomes limitations of the Koppejan model but requires more sensitive parameter tuning to avoid spurious effects of anomalously high creep rates and initial subsidence rates. Total strain ε (relative height loss) of a voxel for a time step $\mathrm{\Delta }t=t^n-t^{n-\mathrm{1}}$ consist of an elastic part and an inelastic part, where the latter follows from a rate-law (viscous behaviour) that is referred to as creep. The model uses three compression parameters: swelling constant a, compression constant b, secondary compression constant c. The elastic strain increment is obtained from

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }{\mathit{\epsilon }}_{\mathrm{e}}=a\ln \left({\displaystyle \frac{{\mathit{\sigma }}^{\prime \left(n\right)}}{{\mathit{\sigma }}^{\prime (n-\mathrm{1})}}}\right)\end{array}$$

where σ^′ is effective stress. Creep strain is governed by intrinsic time

$$\begin{array}{}\text{(2)}& \mathit{\tau }={\mathit{\tau }}_{\mathrm{ref}}{\mathrm{OCR}}^{\frac{b-a}{c}}\end{array}$$

Where $\mathrm{OCR}={\mathit{\sigma }}_{\mathrm{p}}^{\prime }/{\mathit{\sigma }}^{\prime }$ is the overconsolidation, ratio ${\mathit{\sigma }}_{\mathrm{p}}^{\prime }$ the preconsolidation stress, and τ_ref a reference intrinsic time of 1 d.

The creep strain increment is calculated from the following set of relationships

$$\begin{array}{}\text{(3a)}& {\displaystyle }\mathrm{\Delta }{\mathit{\epsilon }}_{\mathrm{cr}}=c\ln \left({\displaystyle \frac{{\mathit{\tau }}^n}{{\mathit{\tau }}^{\ast }}}\right);{\mathit{\tau }}^n={\mathit{\tau }}^{\ast }+\mathrm{\Delta }t;\text{(3b)}& {\displaystyle }{\mathit{\tau }}^{\ast }={\mathit{\tau }}^{n-\mathrm{1}}{\left({\displaystyle \frac{{\mathit{\sigma }}^{\prime (n-\mathrm{1})}}{{\mathit{\sigma }}^{\prime \left(n\right)}}}\right)}^{\frac{b-a}{c}}\end{array}$$

2.3.2 Effective stress development

The Koppejan and the isotache compression models are combined with a module that handles effective stress development. Stresses are evaluated for the centre-depth of voxels. Presently, effective stress calculation uses the degree-of-consolidation approach of Terzaghi (e.g., Verruijt, 2001). The equilibrium effective stress for fully drained (end of primary consolidation) conditions is calculated as the difference of total stress and equilibrium pore pressure

$$\begin{array}{}\text{(4)}& {\mathit{\sigma }}_{\mathrm{eq}}^{\prime }=\mathit{\sigma }-p_{\mathrm{eq}}\end{array}$$

Total stress is obtained from the overburden weight, where specific weight varies per litho-class (sand, clay, peat). A saturated and unsaturated specific weight is specified. Specific weight increases with volume loss by compression. Equilibrium pore pressure, p_eq, is obtained from equilibrium hydraulic head h_eq

$$\begin{array}{}\text{(5)}& p_{\mathrm{eq}}={\displaystyle \frac{\left(h_{\mathrm{eq}}-z\right)}{{\mathit{\gamma }}_{\mathrm{w}}}}\end{array}$$

where γ_w is the specific weight of water and z the elevation head relative to the Dutch ordinance level. Equilibrium head is currently based on linear interpolation between the head of the aquifer which underlies the Holocene confining layer and the momentary phreatic water table. That is, more complex head variation over the Holocene voxel stack in case of vertical seepage in combination with vertically varying hydraulic conductivity is currently neglected. Note that the approach includes effective stress reduction (load reduction) due to drowning; during a stress period in which both water table and aquifer head are constant, the equilibrium pore pressure of the voxels tends to slowly increase due to consolidation-related subsidence which lowers the elevation head z.

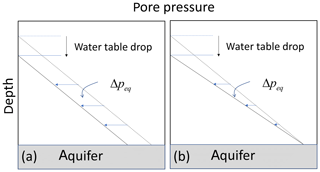
A water table lowering event at the start of a stress period corresponds to a “load” $\mathrm{\Delta }{\mathit{\sigma }}_{\mathrm{eq}}^{\prime }=\mathrm{\Delta }\mathit{\sigma }-\mathrm{\Delta }{p}_{\mathrm{eq}}$. Currently two options are available for the way Δp_eq is handled (Fig. 3). The change in total stress Δσaccounts for the reduction of overburden weight when the unsaturated specific weight is less than the saturated specific weight. In the time steps within the stress period, the load $\mathrm{\Delta }{\mathit{\sigma }}_{\mathrm{eq}}^{\prime }$is gradually transferred to σ^′using the degree-of-consolidation U:

$$\begin{array}{}\text{(6a)}& {\displaystyle }\begin{array}{rl}& {\mathit{\sigma }}^{\prime \left(n\right)}={\mathit{\sigma }}^{\prime (n-\mathrm{1})}+\mathrm{\Delta }U\mathrm{\Delta }{\mathit{\sigma }}_{\mathrm{eq}}^{\prime (n-\mathrm{1})};\\ & \mathrm{\Delta }U=U^{\left(n\right)}-U^{(n-\mathrm{1})}\end{array}\text{(6b)}& {\displaystyle }U\left(t\right)={\left[{\displaystyle \frac{T^{\mathrm{3}}}{T^{\mathrm{3}}+\mathrm{0.5}}}\right]}^{\mathrm{1}/\mathrm{6}};T={\displaystyle \frac{c_{\mathrm{v}}t}{L^{\mathrm{3}}}}\end{array}$$

Where T is the non-dimensional consolidation time, c_v the consolidation coefficient, and L the length scale of two-sided drainage. Presently, L is set equal to the voxel height (which tends to decrease with time).

Figure 3 Change of equilibrium (drained) pore pressure due to a drop of the water table. (a) Aquifer pressure (and head) follows the water table drop. (b) Aquifer pressure (and head) remain stable.

2.4 Oxidation

Oxidation accounts for volume loss of soil layers by mineralization of soil organic matter by oxidation. In Atlantis different approaches/models can be adopted. The most comprehensive model employs an organic-mass based approach. All voxels are initially assigned an organic mass fraction

$$\begin{array}{}\text{(7)}& F_{\mathrm{org}}={\displaystyle \frac{M_{\mathrm{org}}}{M_{\mathrm{org}}+M_{min}}}\end{array}$$

where org and min denote organic and mineral respectively. The organic and the mineral mass content of a voxel (per squaremeter in map view) is calculated from

$$\begin{array}{}\text{(8a)}& {\displaystyle }{M}_{\mathrm{org}}=F_{\mathrm{org}}{\mathit{\rho }}_{\mathrm{bulk}}L\text{(8b)}& {\displaystyle }{M}_{min}=\left(\mathrm{1}-F_{\mathrm{org}}\right){\mathit{\rho }}_{\mathrm{bulk}}L\end{array}$$

where ρ_bulk is the dry bulk density and L is the momentary voxel height. The initial bulk density (kilogram per cubicmeter) is modelled with an empirical relationship obtained from a large set of observational data of Dutch peat samples (Erkens et al., 2016)

$$\begin{array}{}\text{(9)}& {\mathit{\rho }}_{\mathrm{bulk}}={\displaystyle \frac{\mathrm{100}}{F_{\mathrm{org}}}}\left(\mathrm{1}-e^{-F_{\mathrm{org}}/\mathrm{0.12}}\right)\end{array}$$

In each time step Δt, organic mass loss is modelled using a constant rate law for the (part of) voxels that are shallower than a specified height above the MLWT (and not deeper than 1.2 m below land level).

$$\begin{array}{}\text{(10)}& \mathrm{\Delta }{M}_{\mathrm{org}}=-{\mathit{\alpha }}_{m}L\mathrm{\Delta }t\end{array}$$

α_m is an empirical constant estimated from a dataset with subsidence observations over several decades in land subsidence in peat-meadow locations in the Netherlands (Van den Akker et al., 2007). Organic mass loss of a voxel is converted to volume loss (per squaremeter) with

$$\begin{array}{}\text{(11)}& \mathrm{\Delta }{L}^{\mathrm{ox}}=\mathrm{\Delta }{M}_{\mathrm{org}}\widehat{V}\end{array}$$

where $\widehat{V}$ (cubicmeter per kilogram per squaremeter) is called “specific volume of oxidation”. Direct measurements of this quantity do not exist. For high F_org (regular peats) $\widehat{V}$can probably be approximated by the reciprocal of the dry bulk organic matter density. Below F_org≈0.3 (transition to organic rich clays) $\widehat{V}$ is expected to decrease as the bulk volume is more strongly determined by the mineral framework rather than by the organic matter. These concepts are captured in the following relationship

$$\begin{array}{}\text{(12)}& \widehat{V}={\displaystyle \frac{\mathrm{0.5}}{F_{\mathrm{org}}{\mathit{\rho }}_{\mathrm{bulk}}}}\left(\mathrm{1}+\mathrm{erf}\left({\displaystyle \frac{F_{\mathrm{org}}-\mathrm{0.2}}{\mathrm{0.1}}}\right)\right)\end{array}$$

Each time step, M_org and F_org (Eq. 7) are updated for organic mass loss. L is updated both for consolidation and for oxidation Eq. (11). Subsequently, ρ_bulk is updated using

$$\begin{array}{}\text{(13)}& {\mathit{\rho }}_{\mathrm{bulk}}={\displaystyle \frac{M_{\mathrm{org}}+M_{min}}{L}}\end{array}$$

This organic-mass based approach of oxidation provides a consistent framework to account for the mineral content of organic soils. While the organic mass fraction decreases by oxidation, the mineral mass fraction increases, and ultimately a non-oxidizable residue remains. The approach also allows modelling of oxidation-caused subsidence contributions of organic-rich clays and is not limited to oxidation of peat.

3 Modern, open source Python libraries

Atlantis is built on several open source Python libraries, which enormously simplifies development efforts. Python was chosen as the programming language due to its popularity within the scientific community, a comprehensive standard library and a wealth of open source (scientific) libraries. Python's syntax is easy to understand, enabling contributions from researchers, not just professional programmers.

Atlantis has four essential dependencies:

• Numpy (Van der Walt et al., 2011): the basic numerical array package in Python.

• Dask (Dask development team, 2016): dask provides tools for out-of-core (larger than memory) and parallel computation.

• Xarray (Hoyer and Hamman, 2017): xarray brings labelled dimensions and coordinates top of numpy arrays and integrates with dask for parallel computing. Within the context of atlantis, xarray is used primarily for input and output of the simulation data and handles parallel out-of-core computation.

• Numba (Lam et al., 2015): numba translates Python code to optimized machine code. Python code normally runs much slower than compiled languages (sometimes by orders of magnitudes!), but Numba compiled numerical code can approach the speed of C or Fortran.

A simulation can be run by writing a short Python script which initializes and runs the simulation. In this script, the paths to the input data are defined, as well as settings such as time discretization, the type of consolidation method (e.g. Koppejan or isotach), etc.

The input is array based. While two-dimensional data is easily represented by GIS rasters, three-dimensional (voxel) data such as GeoTOP is better represented by a multi-dimensional array data format such as netCDF (Unidata, 2019), HDF5 (The HDF group, 1997–2019), or Zarr (Zarr Development Team, 2019). Xarray is tailored to working with these formats and provides excellent tools to generate input, and to process results; other data formats can easily be converted to generate simulation input using xarray.

Atlantis is organized in three principal data structures. In Python, data structures are represented using objects (within the object-oriented programming paradigm). The object can contain data and procedures; the procedures mutate the data within the object. Different functionalities of the program can be modularized and assigned to these objects, thereby creating a division of responsibilities. In Atlantis, the three principal objects are:

1. The soil column: the soil column simulates one-dimensional subsidence for a single location. Its properties vary only with depth. The soil column contains the numerical methods describing land subsidence.

2. The control unit: the control unit is a collection of soil columns. In reality, many locations with variable subsoils fall within a single management area. Within this area, a single surface water stage is maintained, for example. The control unit is also the building block of parallel execution; multiple control units can be simulated in parallel.

3. The simulation: the simulation is responsible for reading the input data, scheduling parallel execution, and writing the output data.

Object-oriented programming provides re-use of code by inheritance. In Atlantis, we wish to provide multiple consolidation and oxidation methods. These methods differ, but they share a great deal of functionality: read in data and initialize columns, iteratively step through time, compute pressures and stresses, etc. These methods do not have to be duplicated, they can be shared by providing a base class from which they derive shared functionality via inheritance. For example, KoppejanConsolidation and IsotacheConsolidation derive their shared functionality from a common base class.

Nearly all number crunching takes place within the soil column object. Consequently, all soil column procedures are compiled using numba. Unfortunately, numba supports only a subset of the Python language (with a heavy focus on numpy), so some compromises are required. In Atlantis, this mostly consists of converting complex data types to simple arrays and scalars, which are properly understood by numba.