Land subsidence modelling for decision making on groundwater abstraction under emergency situation

This study presents an inversion scheme with uncertainty analysis for a land subsidence modelling by a Monte Carlo filter in order to contribute to the decision-making on the groundwater abstraction. For real time prediction and uncertainty analysis under the limited computational resources and available information in emergency situations, one dimensional vertical land subsidence simulation was adopted for the forward modelling and the null-space Monte Carlo method was applied for the effective resampling. The proposed scheme was tested with the existing land subsidence monitoring data in Tokyo lowland, Japan. The results demonstrated that the prediction uncertainty converges and the prediction accuracy improves as the observed data increased with time. The computational time was also confirmed to be acceptable range for a real time execution with a laptop.

1 Introduction

Groundwater is expected to be one of the alternative water resources to the tap water system under emergency situations such as huge earthquakes. However, the land subsidence caused by the groundwater abstraction is a possible issue, especially in coastal low lands. The groundwater abstraction may mitigate the water resources shortage temporarily while the land subsidence will increase the vulnerability to the flooding in the future. For the decision-making on the groundwater abstraction, the land subsidence modelling with uncertainty analysis can play an important role to predict the future land subsidence under the emergency groundwater abstraction.

Unfortunately, a realistic numerical simulation of land subsidence often requires much effort. First, both the groundwater mass balance and the force equilibrium in the formation have to be simultaneously solved because the land subsidence is a hydro-mechanically coupled process. Second, the spatial resolution of the model for the clayey formations must be high in order to simulate the elastoplastic deformation accurately because of the low hydraulic diffusivity and the hysteretic deformation characteristics of the clay (Aichi, 2008). Additionally, a huge number of forward model runs are often necessary for the uncertainty analysis because the land subsidence model contains many physical parameters and the information on their values in the heterogeneous formations are generally not known.

Emergency situations compound the effort because the computational resources available for the numerical simulation of land subsidence can be limited, and only local data may be available for the modelling because gathering the regional information may be difficult in emergency situation.

Considering these challenges, this study proposes a modelling scheme for a land subsidence prediction with uncertainty analysis under the limited computational resources and information.

2 Method

2.1 Proposed scheme overview and assumed situation for the application

This study assumes the following situations: the pumping and observation wells are constructed at an evacuation location. The observation well monitors the pore pressure of the pumped aquifer and the distance between land surface and the well bottom by extensometer. The geological columns of these wells and the rough estimates for the physical properties of formations are available to develop an initial model with some uncertainty. Electricity is available for running model simulations on a laptop. Because it is a disaster, the government cannot coordinate the different evacuation locations, and then, each evacuation location has to make the decision independently.

Considering these conditions, this study proposes a vertical one dimensional land subsidence simulation to reproduce and predict the land subsidence at the observation well. The boundary condition is specified from the observed pore pressure at the aquifer. A one-dimensional simulation requires less computational efforts than a three-dimensional one. Although three-dimensional simulations are better theoretically, one-dimensional simulations are expected to simulate a major part of the land subsidence process because the groundwater flow in the compacting clayey formations is one dimensional due to the contrast of hydraulic diffusivity between aquifer material and clay (Deming, 2001).

The uncertainty analysis is important for more-informed decision-making. Because many model parameters are uncertain and the observations are limited, the model calibration and the prediction uncertainty analysis should be conducted for highly parameterized model. The Monte Carlo filter method, or particle filter method, for the parameter estimation and uncertainty analysis has been proposed (Kitagawa, 1998; Liu and West, 2001) and applied to the aquifer test problem (Field et al., 2016). However, the number of forward runs can be large if the filtering and resampling are conducted by a neutral distribution such as Liu and West (2001). However, the null-space Monte Carlo method has been used to generate models effectively in the uncertain region in the parameter space (Doherty, 2015). Therefore, this study adopts the null-space Monte Carlo method for the resampling process in the Monte Carlo filter process.

The details of the forward simulation and inversion process are described in the following sections.

2.2 Governing equation for land subsidence simulation

The governing equation for a vertical one-dimensional simulation is a conservation of groundwater mass as follows:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{1}}{\mathrm{1}+e}}{\displaystyle \frac{\partial \left(\mathit{\rho }e\right)}{\partial t}}+{\displaystyle \frac{\partial }{\partial z}}\left[-K\left({\displaystyle \frac{\mathrm{1}}{g}}{\displaystyle \frac{\partial p}{\partial z}}+\mathit{\rho }\right)\right]+\mathit{\rho }Q=\mathrm{0},\end{array}$$

where ρ is the water density, e is the void ratio, K is the hydraulic conductivity, g is the gravitational acceleration, p is the pore pressure, and Q is the volumetric source/sink term. The water density was calculated with the library TEOS-10 ver.3.05 (Intergovernmental oceanographic commission of UNESCO, 2010) for a pure water at 20^∘. In this study, the linear elasticity was assumed for the elastic regime of the deformation. The elastic change in the void ratio, Δe^e, was calculated using the following formula:

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }{e}^e=-{\displaystyle \frac{\mathrm{1}}{K_{\mathrm{v}}}}\left({\mathit{\sigma }}^{\prime }-{\mathit{\sigma }}_{\mathrm{0}}^{\prime }\right)\left(\mathrm{1}+e_{\mathrm{0}}\right),\end{array}$$

where K_v is the uniaxial drained bulk modulus, e₀ is the initial void ratio and ${\mathit{\sigma }}^{\prime }-{\mathit{\sigma }}_{\mathrm{0}}^{\prime }$ denotes the change in the effective stress. Here, the compressional stress is taken to be positive. The effective stress was formulated as:

$$\begin{array}{}\text{(3)}& {\mathit{\sigma }}^{\prime }=\mathit{\sigma }-p,\end{array}$$

where σ is the total stress. The Cam-clay type plasticity (Wood, 1991) was assumed for the plastic regime of the deformation. The plastic change in the void ratio, Δe^p, was calculated by the following formulae:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& \mathrm{\Delta }{e}^p=\\ & \left\{\begin{array}{ll}-C_{\mathrm{c}}{\log }_{\mathrm{10}}\frac{{\mathit{\sigma }}^{\prime }}{{\mathit{\sigma }}_{\mathrm{pc}}^{\prime }}+\frac{\mathrm{1}}{K_{\mathrm{v}}}\left({\mathit{\sigma }}^{\prime }-{\mathit{\sigma }}_{\mathrm{0}}^{\prime }\right)\left(\mathrm{1}+e_{\mathrm{0}}\right)Q& {\mathit{\sigma }}^{\prime }\ge {\mathit{\sigma }}_{\mathrm{pc}}^{\prime }\\ \mathrm{0}& {\mathit{\sigma }}^{\prime }<{\mathit{\sigma }}_{\mathrm{pc}}^{\prime }\end{array},\right.\end{array}\end{array}$$

where C_c is the compression index, and ${\mathit{\sigma }}_{\mathrm{pc}}^{\prime }$ is the preconsolidation stress. Through Eqs. (1)–(4), the solid phase was assumed to be perfectly rigid.

Figure 1 Flowchart of the proposed scheme.

Figure 2 Observed data and model settings for a test at Kameido in Tokyo lowland, Japan.

The fully implicit finite difference method with Newton-Raphson method was applied for numerically solving the nonlinear partial differential equations.

2.3 Boundary and initial conditions

The observed pore pressure of the aquifer is used as the boundary condition at the bottom of the model. The observed pore pressure of the aquifer or the observed recharge rate is used as the boundary condition at the top of the model. The initial pore pressure distribution before the groundwater abstraction is assumed to be hydrostatic. The initial preconsolidation stress is calculated with the past maximum burial depth and assumed hydrostatic pore pressure profile. The initial void ratio distribution is calculated with Eqs. (2) and (3) under the initial pore pressure and the initial preconslidation stress.

2.4 Monte Carlo approach for the filtering and resampling

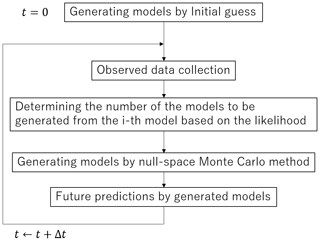
The sequence of parameter estimation and the uncertainty analysis is shown in Fig. 1. At the first phase of each time step, the calculated land subsidence by the models and the observed data are compared, and the values of objective function for the calibration is calculated for each model. In order to filter out the worse models but keep the better models with a certain level of diversity in the resampling process, the number of models to be generated in the resampling phase from each model are set to be proportional to the likelihood as follows:

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{n_i}{N}}\propto \mathrm{Exp}\left(-J_i\right),\end{array}$$

where n_i is the number of models to be generated by the null-space Monte Carlo method from ith model, $N=\sum _i{n}_i$ is the total number of candidate models to be generated, and J_i is the value of the objective function of ith model.

Next, the null-space Monte Carlo method is used to generate the new models and the predictive simulations are conducted by each model. The variation of the predictions gives the uncertainty of the future prediction at the current time step. As the time passes to the next time step of the observation, the above sequence is repeated.

At the first time step, it is important to generate numbers of models of relatively good reproducibility from the initial guess. For this purpose, the singular value decomposition assisted parameter estimation (Doherty, 2015) followed by the null-space Monte Carlo method was used in this study.

For the implementation of the null-space Monte Carlo method and the singular value decomposition assisted parameter estimation, the freely available software PEST (http://www.pesthomepage.org/Home.php, last access: 6 March 2020) was used in this study.

Figure 3 The variety of land subsidence prediction after the calibration in December 1964.

Table 1 Parameter space for a test.

2.5 A test for the proposed scheme

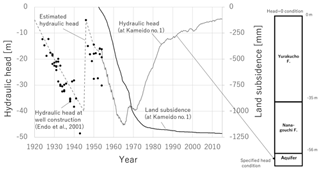
The proposed scheme is tested with the existing data of hydraulic head and land subsidence observed at Kameido No. 1 observation well in Tokyo lowland, Japan. The schematic geological column, the observed hydraulic head, and the land subsidence at Kameido are shown in Fig. 2.

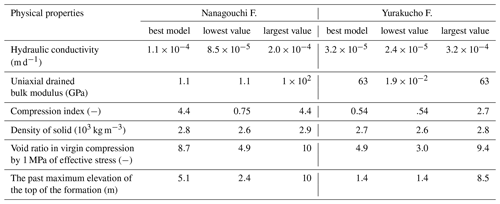
The target formations are Holocene which consist of silty Nanagouchi formation and clayey Yurakucho formation. The formations were discretized to 1 m meshes and the same parameters are assigned for meshes belonging to the same formation.

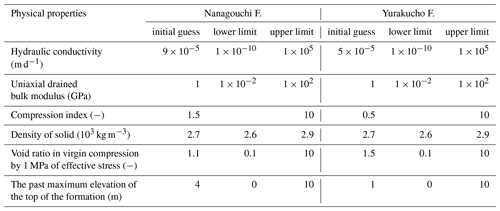
The year 1920 was assumed to be the initial condition before the groundwater abstraction start (Endo et al., 2001; Aichi, 2008). Because the continuous measurement started from June 1952, the hydraulic head before June 1952 was estimated from the records of hydraulic head measured near Kameido (Endo et al., 2001). The objective function for the model evaluation was the square error of the land subsidence. The range of parameter space and initial guess are listed in Table 1.

The proposed scheme was applied from December 1954 and the simulation and calibration time step was one month. The scenario of future pore-pressure change was assumed to be same with the observed hydraulic head after the calibration time step in order to check the prediction accuracy and the uncertainty reduction by comparing the calculated and observed land subsidence. The number of generated models was 50 in this test; however, the methodology to find the optimum number of the models should be examined in a future study.

Table 2 Parameter range of best 5 models after the calibration.

Figure 4 The variety of land subsidence prediction after the calibration in December 1984.

3 Results and discussions

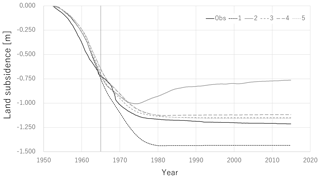
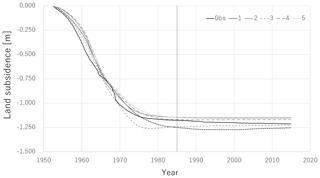
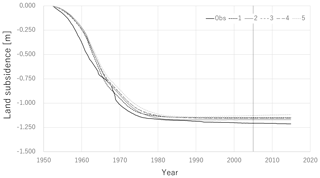
The future predictions by best 5 models at the calibration step in December 1964, December 1984, and December 2004 are shown in Figs. 3 to 5, respectively. In the early stage of the calibration steps, the uncertainty of the future prediction is quite large and the accuracy of prediction is questionable as shown in Fig. 3. However, it was confirmed that the prediction uncertainty decreases and the prediction accuracy improves as additional observation data is included (Figs. 4 and 5). The range of parameters of best 5 models at the calibration step in December 2004 is listed in the Table 2. The parameter uncertainty of hydraulic conductivity and compression index was reduced well while that of the other parameters was not because of less sensitivity.

The computational time was about 10–20 min for each calibration time step with a laptop (NEC LAVIE, Intel Core i7-7500U 2.7GHz, 8GB RAM, Windows 10) and it is considered to be within the acceptable range for decision-makers to use the simulated results in the daily management of groundwater abstraction rate. Although the proposed scheme worked well in this test, there remains several points to be improved.

Figure 5 The variety of land subsidence prediction after the calibration in December 2004.

First, Fig. 5 shows that all models predict slightly smaller land subsidence compared to the actual observation. Currently, the cause of and the countermeasure of this tendency are not clear. It might come from the errors in simulation of the preconsolidation stress which was caused by the uncertainty in the past boundary pore pressure conditions before the continuous measurement started. Not only the physical parameters but also the past pore pressure should be included in the uncertain analysis in a future study. In addition, the current test was limited to the long-term process in several tens of years and the simulation and calibration time step were one month because of the limitation of the published data. However, the actual application is considered to be in more short-term after the event. The examination of the time-step duration is also important in a future study.

4 Conclusions

A numerical scheme for the land subsidence modelling with the visualization of prediction uncertainty is proposed for contributing to the decision-making on the groundwater abstraction in emergency situations. The scheme was based on the Monte Carlo filter approach with one dimensional vertical land subsidence simulation and the null-space Monte Carlo method for generating models. The proposed scheme demonstrated that it can satisfactory reproduce the existing land subsidence data and it is applicable for the real time land subsidence model inversion and the uncertainty analysis. The simulated relation between the pore pressure and the land subsidence is expected to tell the meaning of monitored data at the observation well to the decision-makers. However, further improvements to include the boundary condition uncertainty and the examinations of the performance in the short-term process are necessary in the future study as well as the methodology to find the optimal number of models.