Influence of pore water pressure change on consolidation behavior of saturated poroelastic medium

There are many factors causing land subsidence, and groundwater extraction is one of the most important causes of subsidence. A set of coupled partial differential equations are derived in this study by using the poro-elasticity theory and linear stress-strain constitutive relation to describe the one-dimensional consolidation in a saturated porous medium subjected to pore water pressure change due to groundwater table depression. Simultaneously, the closed-form analytical solutions for excess pore water pressure and total settlement are obtained. To illustrate the consolidation behavior of the poroelastic medium, the saturated layer of clay sandwiched between two sand layers is simulated, and the dimensionless pore water pressure changes with depths and the dimensionless total settlement as function of time in the clay layer are examined. The results show that the greater the water level change in the upper and lower sand layers, the greater the pore water pressure change and the total settlement of the clay layer, and the more time it takes to reach the steady state. If the amount of groundwater replenishment is increased, the soil layer will rebound.

1 Introduction

The consolidation of soil induced by excessive withdrawal of groundwater is a worldwide problem and usually known as land subsidence which has occurred in many cities, for example, Bangkok, Venice, Mexico, Shanghai and so on. Therefore, analyzing and predicting soil consolidation due to groundwater withdrawal in a multiaquifer system is important for achieving the control of land subsidence and the sustainable use of groundwater resource. The most widely used theories of consolidation behavior are Terzaghi (1925) and Biot (1941). The study of consolidation was firstly proposed by Terzaghi (1925) considering the unidirectional consolidation rate of saturated clay layers. Despite the significant advance of this theory in capturing the essence of consolidation process, the coupling between fluid flow and deformation in a fully-saturated porous medium is not truly laid on a firm theoretical base. This conceptual breakthrough was achieved later by Biot (1941), who brought the role of the solid and fluid constituents on equal footing to formulate a pair of coupled equilibrium equations of motion using the displacement vector of solid and fluid pore pressure as dependent variables, now known as poroelasticity. Tuncay and Corapcioglu (1996) used volume-average theory to simulate the consolidation problem of poroelastic media saturated by two immiscible Newtonian fluids. In addition, Luo and Zeng (2011) constructed a coupled three-dimensional model of consolidation and groundwater extraction based on the viscoelastic-plastic constitutive relation and rheological theory of Biot's poroelasticity, and used finite element method to simulate and compare groundwater level changes and soil compression. Lo et al. (2014) have recently developed the poroelasticity theory of three-dimensional consolidation in unsaturated soils, which features the displacement vector of the solid phase together with the excess pore water and air pressures as dependent variables.

Tsai et al. (2006) and Tseng et al. (2008) applied the linear poro-elasticity theory to investigate the soil consolidation of multi-aquifer system caused by groundwater level decline due to pumping, but they didn't consider the viscous coupling caused by viscous drag. Considering the coupling between fluid flow and deformation, we analyze the soil consolidation due to groundwater table depression in a multiaquifer system based on the coupled poroelasticity equations formulated by Lo et al. (2014). After the closed-form analytical solutions for excess pore water pressure together with total settlement are obtained, numerical studies are undertaken for highly permeability porous sand (aquifers) surrounding an impervious clay (aquitard).

2 Governing equations

According to the poroelasticity theory of consolidation developed by Lo et al. (2014), the momentum balance equations for a deformable homogeneous porous medium bearing one compressible, viscous fluid, in the absence of body force and inertial force, can be expressed as

$$\begin{array}{}\text{(1a)}& -R_{\mathrm{22}}\left({\displaystyle \frac{\partial {\mathit{u}}_{\mathrm{f}}}{\partial t}}-{\displaystyle \frac{\partial {\mathit{u}}_{\mathrm{s}}}{\partial t}}\right)=-\mathit{\varnothing }\mathbf{\nabla }{p}_{\mathrm{f}},\end{array}$$

$$\begin{array}{}\text{(1b)}& \mathbf{\nabla }\cdot \stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}=\mathrm{0},\end{array}$$

where the subscripts “s” and “f” represent the solid phase and fluid phase, respectively; ∅ represents the porosity; p_f indicates the gauge pressure (excess pressure); u_f and u_s designate the displacements of each phase; $R_{\mathrm{22}}(=-{\mathrm{\varnothing }}^{\mathrm{2}}{\mathit{\mu }}_{\mathrm{f}}/k_{\mathrm{s}})$ signifies the coefficient of viscous drag due to the velocity difference between solid phase and fluid phase, where μ_f is the dynamic shear viscosity of the fluid phase, k_s is the intrinsic permeability. $\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}$ denotes the total stress tensor for the porous medium, using the sign convention that tension is positive. On the basis of Biot's theory (1962), the total stress components $\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}$ of the bulk material is defined as

$$\begin{array}{}\text{(2)}& \stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}={\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{t}}}_{\mathrm{s}}-\mathit{\varnothing }{p}_{\mathrm{f}}\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{\mathit{\delta }}},\end{array}$$

where ${\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{t}}}_{\mathrm{s}}$ is the stress tensor for the solid phase, $\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{\mathit{\delta }}}$ is the unit tensor.

2.1 Linear stress-strain relations

According to the mass balance equation, the linear stress-strain relations for a porous medium containing single fluid

$$\begin{array}{}\text{(3a)}& {\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{t}}}_{\mathrm{s}}=\mathrm{2}G\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{e}}+(Ae+Q\mathit{\epsilon })\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{\mathit{\delta }}},\end{array}$$

$$\begin{array}{}\text{(3b)}& -\mathrm{\varnothing }{p}_{\mathrm{f}}=Qe+R\mathit{\epsilon },\end{array}$$

where $\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{e}}=\frac{\mathrm{1}}{\mathrm{2}}(\mathbf{\nabla }{\mathit{u}}_{\mathrm{s}}+\mathbf{\nabla }{\mathit{u}}_{\mathrm{s}}^{\mathrm{T}})$ is the solid phase strain tensor, the superscript “T” representing the transpose; G is the shear modulus of porous medium frame; $e=\mathbf{\nabla }\cdot {\mathit{u}}_{\mathrm{s}}$ is the dilatation of solid phase; $\mathit{\epsilon }=\mathbf{\nabla }\cdot {\mathit{u}}_{\mathrm{f}}$ is the dilatation of fluid phase; The elastic coefficients A, Q, and R can be expressed as function of four elastic moduli (see the detail from Lo et al., 2005). After introduction of volume-averaged form and the linear stress-strain relation, Eq. (2) becomes

$$\begin{array}{}\text{(4)}& \stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}=\mathrm{2}G\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{e}}+\mathit{\{}\left(A+Q\right)e+(Q+R)\mathit{\epsilon }\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{\mathit{\delta }}}.\end{array}$$

According to Eq. (3b), the fluid dilatation ε can be expressed in terms of the fluid pressure p_f and the solid dilatation e as

$$\begin{array}{}\text{(5)}& \mathit{\epsilon }={\displaystyle \frac{-Q}{R}}e+{\displaystyle \frac{-\mathit{\varnothing }}{R}}{p}_{\mathrm{f}}=d_{\mathrm{1}}e+d_{\mathrm{2}}{p}_{\mathrm{f}}.\end{array}$$

In Eq. (5), the parameter d₁ is dimensionless, while d₂ has the unit of inverse stress. It is conventional to use stress variables as dependent variables rather than strain variables. Therefore, we take divergence of both sides of Eq. (1a), and then substitute Eq. (5) into the result and obtain:

$$\begin{array}{}\text{(6)}& R_{\mathrm{22}}{d}_{\mathrm{2}}{\displaystyle \frac{\partial p_{\mathrm{f}}}{\partial t}}+(d_{\mathrm{1}}-\mathrm{1}){\displaystyle \frac{\partial e}{\partial t}}=\mathit{\varnothing }{\mathrm{\nabla }}^{\mathrm{2}}{p}_{\mathrm{f}}.\end{array}$$

In the same spirit, the linear stress-strain relation can be written as:

$$\begin{array}{}\text{(7)}& \stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}=\mathrm{2}G\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{e}}+\mathit{\{}\left[A+Q+\left(Q+R\right)d_{\mathrm{1}}\right]e+(Q+R)d_{\mathrm{2}}{p}_{\mathrm{f}}\stackrel{\mathrm{‾}}{\stackrel{\mathrm{‾}}{\mathit{\delta }}}.\end{array}$$

For a one-dimensional problem with a time-invariant total compaction stress, Eqs. (6) and (7) can be reduced to

$$\begin{array}{}\text{(8a)}& d_{\mathrm{2}}{\displaystyle \frac{\partial p_{\mathrm{f}}}{\partial t}}+(d_{\mathrm{1}}-\mathrm{1}){\displaystyle \frac{{\partial }^{\mathrm{2}}w}{\partial t\partial z}}={\displaystyle \frac{\mathit{\varnothing }}{R_{\mathrm{22}}}}{\displaystyle \frac{{\partial }^{\mathrm{2}}{p}_{\mathrm{f}}}{\partial z^{\mathrm{2}}}},\end{array}$$

$$\begin{array}{}\text{(8b)}& \mathrm{0}=\left[\mathrm{2}G+A+Q+\left(Q+R\right)d_{\mathrm{1}}\right]{\displaystyle \frac{\partial w}{\partial z}}+\left[\left(Q+R\right)d_{\mathrm{2}}\right]p_{\mathrm{f}},\end{array}$$

where w is the component of the displacement of vector of the solid phase in the z direction. Equation (8b) can be rearranged as

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\partial w}{\partial z}}=-{\displaystyle \frac{(Q+R)d_{\mathrm{2}}}{K^{\left(u\right)}}}{p}_{\mathrm{f}},\end{array}$$

where $K^{\left(u\right)}=[\mathrm{2}G+A+Q+(Q+R\left)d_{\mathrm{1}}\right]$. Thus, the term $\frac{\partial w}{\partial z}$ in Eq. (8a) can be replaced by Eq. (9) to yield the following coupled partial differential equation

$$\begin{array}{}\text{(10)}& q_{\mathrm{1}}{\displaystyle \frac{\partial p_{\mathrm{f}}}{\partial t}}=b_{\mathrm{1}}{\displaystyle \frac{{\partial }^{\mathrm{2}}{p}_{\mathrm{f}}}{\partial z^{\mathrm{2}}}},\end{array}$$

where the parameters q₁ and b₁ are defined as

$$\begin{array}{}\text{(11a)}& q_{\mathrm{1}}=\left(d_{\mathrm{2}}-{\displaystyle \frac{(d_{\mathrm{1}}-\mathrm{1})(Q+R)d_{\mathrm{2}}}{K^{\left(u\right)}}}\right),\end{array}$$

$$\begin{array}{}\text{(11b)}& b_{\mathrm{1}}={\displaystyle \frac{\mathit{\varnothing }}{R_{\mathrm{22}}}}={\displaystyle \frac{-k_{\mathrm{s}}}{\mathit{\varnothing }{\mathit{\mu }}_{\mathrm{f}}}},\end{array}$$

Equations (10) represent a one-dimensional poroelastic problem of consolidation caused by pore water pressure changes. Coupling occurs only in the first-order time-derivative term of the pore water pressure. The diffusivity coefficient $c_v=b_{\mathrm{1}}/q_{\mathrm{1}}$ denotes the coefficient of consolidation.

2.2 Boundary and initial conditions

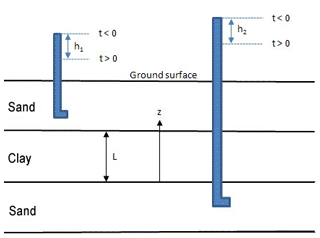
A stratum of clay sandwiched between sandy strata that are highly permeable and much stiffer than the clay is shown in Fig. 1, water level depression h₁ and h₂ due to pumping take place in the sandy strata above and below the clay. Due to significant differences of permeability and compressibility between sand and clay, excessive pore pressure only exists in the clay as consolidation proceeds. And nearly all of the consolidation happens due to the volume change within the clay, while the sandy strata may be considered rigid media as compared with the clay. Furthermore, the steady-state solutions, which are usually applied in engineering practice, will be considered.

Figure 1 Sketches of soil consolidation due to water table depression.

The initial conditions can be expressed as $p_{\mathrm{f}}(z,\mathrm{0})=\mathrm{0}$. With respect to the boundary conditions, the top and bottom surfaces of the porous layers are considered to be permeable so that the pore fluids can drain at both sides of the sample, which leads to $p_{\mathrm{f}}\left(\mathrm{0},t\right)=-{\mathit{\rho }}_{\mathrm{f}}g{h}_{\mathrm{2}}$ and $p_{\mathrm{f}}\left(L,t\right)=-{\mathit{\rho }}_{\mathrm{f}}g{h}_{\mathrm{1}}$. Based on Tsai et al. (2006), combined flow equation and Darcy's law and assuming an isotropic and homogeneous porous media and one-dimensional steady-state consolidation, the pore water pressure in the clay stratum can be represented as function of depth as $p_{\mathrm{f}}=-{\mathit{\rho }}_{\mathrm{f}}g[h_{\mathrm{2}}+z(h_{\mathrm{1}}-h_{\mathrm{2}})/L]$. By combining of initial and boundary equations into Eq. (10), we can get

$$\begin{array}{}\text{(12)}& {\displaystyle }\begin{array}{rl}{p}_{\mathrm{f}}\left(z,t\right)& ={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{f}}g\left[-h_{\mathrm{2}}L+z\left(h_{\mathrm{2}}-h_{\mathrm{1}}\right)\right]}{L}}\\ & +\sum _{n=\mathrm{1}}^{\mathrm{\infty }}{\displaystyle \frac{\mathrm{2}{\mathit{\rho }}_{\mathrm{f}}g}{n\mathit{\pi }}}\left[h_{\mathrm{2}}-h_{\mathrm{1}}\cos \left(n\mathit{\pi }\right)\right]\sin \left({\displaystyle \frac{n\mathit{\pi }z}{L}}\right)\cdot e^{-c_v(\frac{n\mathit{\pi }}{L}{)}^{\mathrm{2}}t}.\end{array}\end{array}$$

The time-dependent total settling s(t) can be consequently deduced

$$\begin{array}{}\text{(13)}& {\displaystyle }\begin{array}{rl}s\left(t\right)& =-\underset{\mathrm{0}}{\overset{L}{\int }}{\displaystyle \frac{\partial w}{\partial z}}\mathrm{d}z={\displaystyle \frac{-\left[\left(Q+R\right)d_{\mathrm{2}}\right]{\mathit{\rho }}_{\mathrm{f}}g(h_{\mathrm{1}}+h_{\mathrm{2}})L}{\mathrm{2}{K}^{\left(u\right)}}}\\ & +{\displaystyle \frac{(Q+R)d_{\mathrm{2}}{\mathit{\rho }}_{\mathrm{f}}g}{K^{\left(u\right)}}}\\ & \times \sum _{n=\mathrm{1}}^{\mathrm{\infty }}{\displaystyle \frac{\mathrm{2}L(\mathrm{1}-\cos \left(n\mathit{\pi }\right))(h_{\mathrm{2}}-h_{\mathrm{1}}\cos (n\mathit{\pi }\left)\right)}{(n\mathit{\pi }{)}^{\mathrm{2}}}}\cdot e^{-c_v(\frac{n\mathit{\pi }}{L}{)}^{\mathrm{2}}t}.\end{array}\end{array}$$

Equation (13) implies that, as for t→∞, the final total settlement Δs is equal to

$$\begin{array}{}\text{(14)}& \mathrm{\Delta }s=-(Q+R)d_{\mathrm{2}}{\mathit{\rho }}_{\mathrm{f}}g\left[\right(h_{\mathrm{1}}+h_{\mathrm{2}}\left)L\right]/\left(\mathrm{2}{K}^{\left(u\right)}\right).\end{array}$$

3 Numerical results and discussions

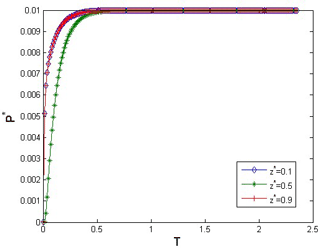
In order to investigate quantitatively the deformation of porous media due to water table depression, the governing equations have been implemented in MATLAB and a textbook case is simulated. The ground parameters used in the study are summarized in Table 1, which also lists the numerical value of elastic coefficients and hydraulic parameters necessary for the numerical simulations performed in the present study. Before the consolidation of soil subjected to water level depression is examined, the implementation of the poroelastic consolidation is verified. Considering water level depressions $h_{\mathrm{1}}/L=h_{\mathrm{2}}/L=\mathrm{0.01}$ and elapsed dimensionless time $T=c_{v}t/L^{\mathrm{2}}$, the excess dimensionless pore water pressure $P^{\ast }(=p_{\mathrm{f}}(zt)/({\mathit{\rho }}_{\mathrm{f}}gL\left)\right)$ with respect to the dimensionless depth $Z^{\ast }(=z/L)$ are shown in Fig. 2. The pore water pressure increases with time at the inside of the clay stratum. Because the boundary of clay stratum is subjected to a constant water table depression, the dimensionless pore water pressure at top and bottom of clay stratum remains equal to the value caused by the water table depression. The dimensionless pore water pressure at different depth for various dimensionless elapsed times is also plotted in Fig. 3. The dimensionless pore water pressure near the boundary is greater than that near the center of stratum. The change of pore water pressure in the clay layer is directly related to pressures at the upper and lower boundaries resulting from pumping, and the change of pore water pressure is from the boundary to the medium of the layer.

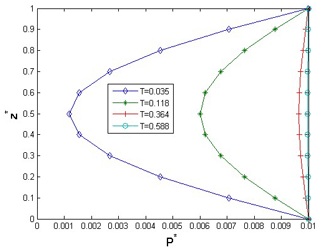
Figure 2 The dimensionless pore water pressure with respect to the dimensionless depth at different elapsed times.

Figure 3 The dimensionless pore water pressure at different depths versus time.

Table 1 Material parameters for saturated clay (Rawls et al., 1992; Lo et al., 2007).

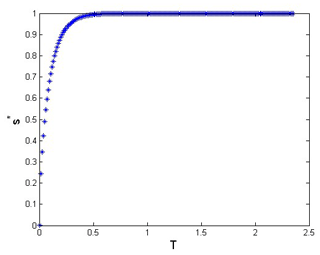
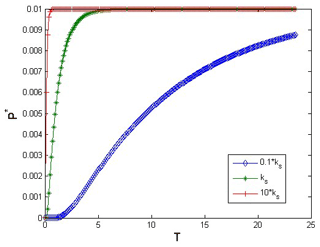
Figure 4 shows the dimensionless settlement $s^{\ast }(=\mathrm{s}(t)/\mathrm{\Delta }s)$ with respect to the dimensionless elapsed time. We can easily calculate the quantity of settlement at any time from Fig. 4. The dissipation of pore water pressure is significantly influenced by permeability (Fig. 5). When the intrinsic permeability is higher, the pore water pressure reaching stabilize is faster.

Figure 4 The dimensionless surface settlement versus time.

Figure 5 Effect of permeability on the dissipative pore water pressure as function of time.

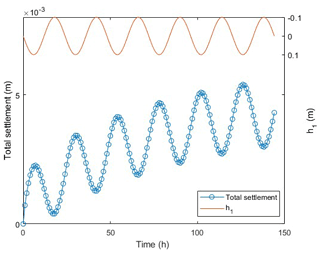
Considering the current situation, the groundwater table may be a time series change. The upper water level changes with time was assumed as $h_{\mathrm{1}}=\mathrm{0.1}\times \sin \left(\frac{t\mathit{\pi }}{\mathrm{12}}\right)m$ (the time interval is 1 h, so the water level changes for 12 h as a cycle), lower water level changes do not change with time $h_{\mathrm{2}}/L=\mathrm{0.02}$. It can be clearly seen from the results in Fig. 6 that because of the greater fluctuation of the fixed water level at the lower boundary, the trend of the consolidation with time is similar to the above-mentioned fixed water level fluctuation, but at the same time, it is affected by the fluctuation of the upper water level, and the periodic fluctuation appears. When the upper groundwater table raises, the settlement significantly decreases, which is regarded as the phenomenon of soil swelling. It can also be seen that the amount of rebound is less than that of compression. Therefore, increasing the groundwater replenishment from land subsidence prevention, the soil layer will partially rebound.

4 Conclusions

A set of coupled partial differential equations are presented in this study by using the poro-elasticity theory and linear stress-strain constitutive relation to describe the one-dimensional consolidation in a saturated porous medium subjected to pore water pressure change due to groundwater table depression. Simultaneously, the closed-form analytical solutions for excess pore water pressure together with total settlement are written. To quantitatively analyze the consolidation behavior of the poroelastic medium, a saturated layer of clay sandwiched between two sand layers is taken as example, and the dimensionless pore water pressure changes with depth and the dimensionless total settlement as a function of time in the clay layer are examined. The results show that the greater the water level change in the upper and lower sand layers, the greater the pore water pressure change and the total settlement of the clay layer are, and the more time it takes to reach the steady state. The change of pore water pressure in the clay layer is directly related to the pumping in the upper and lower boundaries, and the change of pore water pressure is from the boundary to the medium of the layer. When the groundwater table rises again, the phenomenon of soil swelling appears. If the amount of groundwater replenishment is increased, the soil layer will rebound partially.

Figure 6 The total settlement caused by fluctuating water level at the top clay boundary versus time (the water table depression at the base of the clay layer is kept constant in time ($h_{\mathrm{2}}/L=\mathrm{0.02}$).