the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Absolute vertical motion of the Amsterdam Ordnance Datum (NAP)
Rene Reudink
Roland Klees
Bas Alberts
Pieter van Waarden
The backbone of the Amsterdam Ordnance Datum (NAP) is a network of about 400 primary subsurface markers. Relative movements between the primary subsurface markers are measured with spirit levelling once in 10–20 years. However, little is known about absolute vertical movements of the primary network. This information is indispensable for the interpretation of water level measurements at the tide gauges along the Dutch coast. It may be provided by gravity measurements.
Here we present a time-series analysis of more than twenty years of gravity measurements at the stations Westerbork, Epen, Zundert, and Radio Kootwijk. It reveals that only station Epen shows a statistically significant movement of µGal yr−1, which corresponds to an uplift of 1.3±0.5 mm yr−1. For the other stations, the trends are statistically not different from zero at a significance level of 0.05. Corrections for water table variations are found to be indispensable; peak-to-peak amplitudes range from 4 µGal (Westerbork) to 28 µGal (Radio Kootwijk). Depsite some fundamental objections, corrections for instrumental offsets reduce the data scatter. First experiments with 7 years of soil moisture data acquired at station Radio Kootwijk reveal that the gravity signal of soil moisture variations has a standard deviation of 2.2 µGal, which is comparable to the noise standard deviation of measured gravity.
- Article
(207 KB) - Full-text XML
- BibTeX
- EndNote
The heights of the ∼35 000 markers of the second-order NAP network are determined with respect to a primary network of about 400 underground markers, which form the backbone of NAP. These underground markers are directly connected to the top of the Pleistocene sediment layers, which at the time of their construction, was believed to be stable, i.e., without significant vertical movement. However, geological studies indicate vertical movements of the Pleistocene sediment layers of different origins (e.g., Kooi et al., 1998). These vertical movements are the reason why over regular intervals of about 10–20 years, the primary network of sub-surface markers is re-measured. Though this cannot provide information about the absolute vertical motion of the NAP, it provides information about differences in vertical movements rates between sub-surface markers. These re-measurement campaigns are sufficient for the primary task of NAP. This does not apply, however, if NAP is used to determine absolute vertical land motion at the location of tide gauge stations. This specific application of NAP is necessary to separate the steric and eustatic component of sea level rise from the vertical land motion at the site. The separation is needed among others to validate climate models on which predictions of future sea level rise are based.
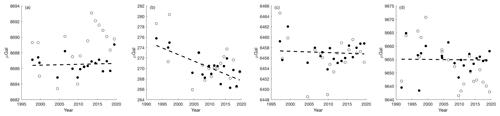
Figure 1Pre-processed gravity data before (circles) and after (dots) corrections for offset and estimated water table variations were applied. The dashed line shows the estimated linear trend based on offset and water table corrected pre-processed gravity data. From (a) to (d): Westerbork, Epen, Zundert, Radio Kootwijk
Global Navigation Satellite Systems (GNSS) can provide information about vertical movements relative to a network of reference stations. However, long-term monitoring of the vertical movements using GNSS suffers among others from terrestrial reference frame issues (in particular centre of mass movements) and low-frequency (flicker) noise.
Here we use gravity measurements to monitor the long-term absolute vertical movement of the NAP. This movement is not constant over the country, but may have long-wavelength patterns. Complex spatial patterns would require a significant number of gravity stations. However, as long as the regular re-measurements of the primary NAP network using spirit levelling are continued, a single gravity station is already enough. To create redundancy, a network of six stations has been established where absolute vertical movements are determined from a time series of yearly gravity measurements.
Here, we present an analysis of the data records at four stations, which cover at least 20 years of data. In Sect. 2, we describe the network of absolute gravity stations, the chosen measurement setup, and the data pre-processing. The methodology of data analysis is the subject of Sect. 3. The results, in particular the estimated vertical rates, are the subject of Sect. 4. In Sect. 5, we conclude by emphasising the main findings and identifying topics for future research.
The absolute gravity network comprises the stations Radio Kootwijk (1991–today), Epen (1992–today), Zundert (1996–today), Westerbork (1998–today), Oudemirdum (2012–today), and Oudeschild (2014–today). All stations, except Epen (which is located on a rock formation from the Carboniferous), are located on the top of the Pleistocene sediment layer (2.58 Ma–11.7 ka BP). The stations Oudeschild (Texel), Oudemirdum, and Westerbork are located on the Drenth-Frisian boulder clay plateau, a glacial deposit from the second-last ice age (Saalian, 370 ka–130 ka BP). Radio Kootwijk is located on top of a moraine from the penultimate ice age (Saalien, 370 ka–130 ka BP). Zundert is founded on a layer of surface sand from the early to mid Pleistocene.
Most gravity measurements were taken with Micro-g FG-5 absolute gravimeters. Before 2007, they were operated by the Bundesamt für Kartographie and Geodäsie (FG5 # 101; 1996), the Royal Observatory of Belgium (FG-5 # 202; 1997), and the University of Luxembourg (FG-5 # 216; 2004–2007), respectively. Since 2007, all measurements are being done with the FG-5 # 234, operated by TU Delft. The FG-5 is a free-fall class of absolute gravimeter, which measures the position and time since the start of the drop of a free-falling test mass. Gravity is then estimated by fitting a model of the equation of motion to the data. The measurements were organised in sets, where each set comprises 100–200 free-fall experiments (drops). Typically, 12 sets were measured during night to minimise micro-seismic background noise at frequencies below 1 Hz, which is mainly caused by ocean waves along the west-European coast and local wind. At stations with an increased background noise level such as Oudeschild, 24–48 sets were measured to obtain a measurement precision comparable with the other stations.
The data pre-processing follows international processing standards and comprises corrections for Earth tides, ocean loading, atmospheric pressure effects, and polar motion. There are no standards to correct gravity for hydrological signals (e.g., water table and soil moisture variations, precipitation and snow) as the corrections depend on a number of station-specific hydrological settings, which are difficult to generalise, and not all hydrological parameters are monitored. Therefore, water table measurements were done in wells located in the immediate vicinity of the gravity station (except station Epen), and a Bouguer plate model was used to compute the gravity signal of water table variations (cf. Sect. 3). Experimental soil moisture data were acquired since 2013 using the well at station Radio Kootwijk with an in-house developed and calibrated soil moisture sensor. This sensor was specially designed to fit in the most commonly used monitoring well types. Water table and soil moisture measurements were always made on the day of the absolute gravity measurements.
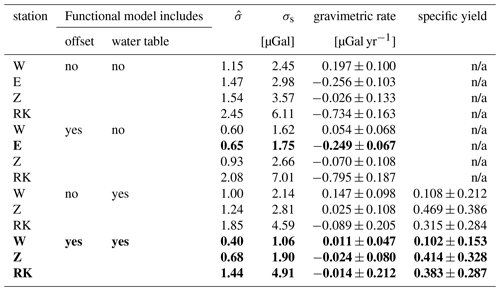
Table 1Results of the analysis of the gravity records at stations Westerbork (W), Epen (E), Zundert (Z), and Radio Kootwijk (RK). is the a-posteriori standard deviation of unit weight; σs is the RMS scatter around the estimated trend of the pre-processed gravity data corrected for instrumental offset (if offset = “yes”) and water table variations (if water table = “yes”). The given uncertainties for the gravimetric rate and the specific yield are a-posteriori standard deviations. The preferred solutions are highlighted in bold.
n/a: not applicable.
We use the functional model
to analyse the gravity time series at a station. E is the mathematical expectation operator, g(t) is pre-processed gravity at epoch t, t0 is a reference epoch, e.g., t0 = t1, o(t) is the gravimeter offset, a and b are the two parameters defining a linear trend model, and w(t) is the gravity signal of water table variations. The term is referred to as the trend function, and the parameter b is referred to as the gravimetric rate.
Gravimeter offsets are taken from the International Comparisons of Absolute Gravimeters (ICAGs) campaigns, which are organised once in 3–5 years by the Working Group on Gravimetry of the Consultative Committee on Mass (CCM WGG) and the Study Group 2.1.1 on Comparison of Absolute Gravimeters (SGCAG) of Sub-Commission 2.1 of the International Association of Geodesy (IAG) and the Bureau International des Poids et Mesures (BIPM). During these campaigns, the participating absolute gravimeters are compared to one another, and an offset is estimated per instrument relative to the weighted mean over all instruments (e.g., Vitushkin et al., 2010; Francis and Baumann, 2012).
Water table variations are recorded in wells located nearby the absolute gravity station. Except for station Epen, the area in the vicinity of the gravity stations is flat. Therefore, we use a simple Bouguer plate model,
where n is the specific yield, which is considered as one of the unknown parameters to be estimated from the data, h(t) is the level of the water table with respect to the Earth's surface, measured positively upwards, and h0 is a reference water table value, e.g., h0 = h(t1). The model of Eq. (2) is not suited for station Epen. Here, the groundwater flow is very complex due to the hilly topography and the presence of a nearby steep slope to the river valley of the Geul. As no suitable hydrological model is available, no water table corrections were computed for station Epen. The results of Sect. 4 confirm this choice.
The parameters of the functional model of Eq. (1) are estimated using weighted least-squares. The weight of an observation zi is chosen inversely proportional to its noise variance. The variance is computed as
where σuu is the unified uncertainty of the absolute gravimeter, is the internal measurement precision (experimental standard deviation) of gravity at epoch ti, and is the standard deviation of the offset at epoch ti. The unified uncertainty comprises the known systematic errors for the absolute gravimeter and the errors of the geophysical models applied to the data during data pre-processing. For the FG-5, the current value, adopted by the international community, is σuu = 2.1 µGal (Francis et al., 2015). is determined from the drop scatters (cf. Sect. 2) using the law of covariance propagation. Values strongly depend on the background noise and range from 0.17–2.7 µGal. The standard deviations of the offsets are taken from the results of the ICAGs. They range from 1.83–2.87 µGal. For station Westerbork, the stochastic model of Eq. (3) is extended by adding the variance of mass variations in the soil on top of the roof and the side walls of the gravity bunker, which are caused by variations in the amount of water in the soil. A Monte-Carlo simulation with a finite element model of the gravity bunker, showed that the signal's standard deviation is about 0.46 µGal.
For each station, we analysed the time series of absolute gravity measurements. We computed solutions with and without offset corrections and/or water table regression term, respectively. There are two reasons for that. Firstly, the instrumental offsets of an absolute gravimeter were determined relative to the other gravimeters participating in the calibration campaigns as outlined in Sect. 3. However, not the same gravimeters participated in each campaign, operators changed, and the uncertainties of the estimated offsets are pretty large, sometimes larger than the offsets. Therefore, it needs to be seen whether applying offset corrections provides more accurate gravimetric rates. Secondly, the specific yield of the soil around each station has to be estimated from the data. It has to be seen whether specific yield estimates are reasonable, and how strong they are correlated with the gravimetric rates. Each analysis is complemented by various statistical hypotheses tests, among others an overall test of the functional and stochastic model and a Pope test for outlier detection (e.g., Koch, 1999).
Figure 1 shows the pre-processed gravity data before and after corrections for offset and estimated water table variations were applied. The latter reduces the scatter of the data for all stations; the most significant reduction is obtained for stations Westerbork, Zundert, and Kootwijk. Table 1 shows the gravimetric rates and some other statistics. When applying offset corrections, the a posteriori standard deviation of unit weight () decreases by a factor ranging from 1.2 (Radio Kootwijk) to 2.3 (Epen). Accounting for water table variations reduces by a factor of 1.2–1.3 for stations Westerbork, Zundert, and Radio Kootwijk. The smallest is obtained when both instrumental offsets and water table corrections are applied. Compared to a solution without these corrections, the improvement factors range from 1.7 (Radio Kootwijk) to 2.9 (Westerbork). Moreover, these solutions always provided the smallest a posteriori standard deviations of the estimated gravimetric rates and specific yields, respectively. In addition, the over model tests were accepted at a significance level of 0.001, which was not always the case if at least one of these corrections was omitted. Finally, no outliers in the data were detected at a significance level of 0.017. Therefore, we prefer the solution with offset and water table corrections.
Using a significance level of 0.05, the null hypothesis of a zero gravimetric rate was accepted for all stations, except Epen. For Epen, the gravimetric rate was found to be µGal. Assuming that the gravimetric rate is only due to a vertical motion of the station, we interpret that station Epen is moving upwards with a rate of 1.3±0.5 mm yr−1.
The analysis of the Radio Kootwijk data record shows some peculiarities. The a posteriori standard deviation of unit weight is a factor of 2 or more larger than for any other station. The correlation coefficient between specific yield and gravimetric rate is unusually high (0.79 compared to 0.20 for Westerbork and Zundert). Finally, the benefit of applying corrections for instrumental offsets is the smallest among all stations. These particularities may point to un-modelled environmental signals in the data. One candidate is soil moisture as the water table at Radio Kootwijk is located at a depth of about 17 m below the surface. Since 2013, we operate an in-house developed and calibrated soil moisture sensor in a tube located nearby the gravity station. Though the data record is still too short to be used for trend estimation, an analysis of the soil moisture data record provides an idea about its gravimetric signal. The mean value of the latter was found to be 46.8 µGal over the period 2013–2019. However, for trend estimation, only variations in soil moisture are relevant. A value of 2.2 µGal was found for the standard deviation of the soil moisture correction. This is comparable to the noise standard deviation of an FG-5 gravity measurement. Hence, soil moisture cannot explain alone the peculiarities of the Radio Kootwijk data record.
We analysed more than 20 years of absolute gravity measurements at the stations Westerbork, Epen, Zundert, and Radio Kootwijk. So far, a statistically significant vertical movement could only be detected for station Epen. The data record at Radio Kootwijk requires further analysis with emphasis on un-modelled environmental signals. A comparison with available GPS time series at the stations Westerbork and Eijsden (14 km west of Epen), a co-location with GPS at the other stations, and a comparison with geological models of movements of the top of the Pleistocene sediment layer is left for future work.
All data used in our study can be accessed at: https://doi.org/10.4121/uuid:1174de8d-32ba-4583-a2e3-2b597453a30b (Reudink and Klees, 2020).
RR operated all instruments in the field and did the data pre-processing; RK did the data processing and wrote the draft paper; RR and RK did the data analysis and interpretation; BA and PvW provided financial support. RR, BA and PvW provided comments to the draft paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “TISOLS: the Tenth International Symposium On Land Subsidence – living with subsidence”. It is a result of the Tenth International Symposium on Land Subsidence, Delft, the Netherlands, 17–21 May 2021.
Francis, O. and Baumann, H.: Final report of the regional key comparison EURAMET, M.G-K1: European Comparison of Absolute Gravimeters ECAG-2011, Metrologia, 49, 07014, https://doi.org/10.1088/0026-1394/49/1a/07014, 2012. a
Francis, O., Baumann, H., Ullrich, C., Castelein, S., Camp, M. V., de Sousa, M. A., Melhorato, R. L., Li, C., Xu, J., Su, D., Wu, S., Hu, H., Wu, K., Li, G., Li, Z., Hsieh, W.-C., Plinks, P. V., Kostelecký, J., Mäkinen, J., Näränen, J., Merlet, S., Santos, F. P. D., Gillot, P., Hinderer, J., Bernard, J.-D., Moigne, N. L., Fores, B., Gitlein, O., Schilling, M., Falk, R., Wilmes, H., Germak, A., Biolcati, E., Origlia, C., Iacovone, D., Baccaro, F., Mizushima, S., Plaen, R. D., Klein, G., Seil, M., Radinovic, R., Sekowski, M., Dykowski, P., Choi, I.-M., Kim, M.-S., Borreguero, A., Sainz-Maza, S., Calvo, M., Engfeldt, A., Agren, J., Reudink, R., Eckl, M., van Westrum, D., Billson, R., and Ellis, B.: CCM.G-K2 key comparison, Metrologia, 52, 07009, https://doi.org/10.1088/0026-1394/52/1a/07009, 2015. a
Koch, K.-R.: Parameter estimation and Hypothesis Testing in Linear Models, Springer Berlin Heidelberg, ISBN 978-3-662-03976-2, 334 pp., 1999. a
Kooi, H., Johnston, P., Lambeck, K., Smither, C., and Moldenijk, R.: Geological causes of recent (100 yr) vertical land movement in the Netherlands, Tectonophysics, 299, 297–316, https://doi.org/10.1088/0026-1394/49/6/666, 1998. a
Reudink, R. H. C. and Klees, R.: Supplementary data: Absolute vertical motion of NAP, 4TU, Centre for Research Data, Dataset, https://doi.org/10.4121/uuid:1174de8d-32ba-4583-a2e3-2b597453a30b, 2020.
Vitushkin, L., Jiang, Z., Robertsson, L., Becker, M., Francis, O., Germak, A., D'Agostino, G., Palinkas, V., Amalvict, M., Bayer, R., Biler-Koivula, M., Desogus, S., Faller, J., Falk, R., Hinderer, J., Gagnon, C., Jokob, T., Kalish, E., Kostelecky, J., Lee, C., Liard, J., Lokshyn, Y., Luck, B., Mäkinen, J., Mizushima, S., Moigne, N. L., Nalivaev, V., Origlia, C., Pujol, E., Richard, P., Ruess, D., Schmerge, D., Stus, Y., Svitlov, S., Thies, S., Ullrich, C., van Camp, M., Vitushkin, A., and Wilmes, H.: Results of the Seventh International Comparison of Absolute Gravimeters ICAG-2005 at the Bureau International des Poids et Mesures, Sevres, in: Gravity, Geoid and Earth Observation, edited by: Mertikas, S., International Association of Geodesy Symposia 135, Springer Berlin Heidelberg, 47–53, 2010. a





