the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Study on the water resources optimal operation based on riverbed wind erosion control in West Liaohe River plain
Sun Wanguang
Li Chengzhen
Fan Baoshan
Rivers are drying up most frequently in West Liaohe River plain and the bare river beds present fine sand belts on land. These sand belts, which yield a dust heavily in windy days, stress the local environment deeply as the riverbeds are eroded by wind. The optimal operation of water resources, thus, is one of the most important methods for preventing the wind erosion of riverbeds. In this paper, optimal operation model for water resources based on riverbed wind erosion control has been established, which contains objective function, constraints, and solution method. The objective function considers factors which include water volume diverted into reservoirs, river length and lower threshold of flow rate, etc. On the basis of ensuring the water requirement of each reservoir, the destruction of the vegetation in the riverbed by the frequent river flow is avoided. The multi core parallel solving method for optimal water resources operation in the West Liaohe River Plain is proposed, which the optimal solution is found by DPSA method under the POA framework and the parallel computing program is designed in Fork/Join mode. Based on the optimal operation results, the basic rules of water resources operation in the West Liaohe River Plain are summarized. Calculation results show that, on the basis of meeting the requirement of water volume of every reservoir, the frequency of reach river flow which from Taihekou to Talagan Water Diversion Project in the Xinkai River is reduced effectively. The speedup and parallel efficiency of parallel algorithm are 1.51 and 0.76 respectively, and the computing time is significantly decreased. The research results show in this paper can provide technical support for the prevention and control of riverbed wind erosion in the West Liaohe River plain.
- Article
(986 KB) - Full-text XML
- BibTeX
- EndNote
With the development and utilization of water resources, partial rivers were dried up in arid or semi-arid area. After dried up, bare riverbed becomes the new cradle land of sandstorm. Since 1972, the lower reaches of the Yellow River has began to dry up (Gao, 1998). The reasons for dry up in the watershed of the Yellow River can be concluded into three aspects: (1) natural reasons, the Yellow River basin is located in an arid and semi-arid region, at the same time, the river dry up may be aggravated by global warming; (2) human activities, about 30 billion m3 runoff were consumed annually (Fu and Chen, 2006), and large-scale soil and water conservation measures decreased the streamflow (Shi et al., 2016). The dry up of river basin has caused many serious problems, such as agricultural and industrial output reduction, environmental degradation and water quality deterioration (Fu and Chen, 2006; Wang and Li, 2007).
Table 1The statistical results about runoff of each hydrological station in the West Liaohe River Plain.
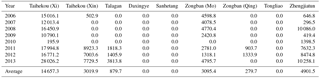
Units: 104 m3.
Wind erosion caused soil loss and then impoverishes lands (Lal, 2001). The blown dust emission from eroding lands impairs air quality (Lee et al., 2003) and poses a threat to human health (Wilson and Sprengler, 1996). The research of wind erosion prevention and control is mainly focused on the following two aspects: (1) the nonerodible grains are placed on the erodible surface to reduce the degree of wind erosion (Bagnold, 1941); (2) the use of vegetation cover or crop residues to prevent wind erosion (Englehorn et al., 1952; Zhang et al., 2003; Jia et al., 2015). The wind erosion control of bare riverbed or lakebed is quite different from sand land. Due to the technical difficulties, it is hard to implement these measures. Bao et al. (2006) estimated the rational water area and inflow of the Ebinur Lake for controlling wind erosion in the dried up lake basin (Bao et al., 2006). For intermittent dried up reach, there is no better erosion control measures so far.
In this paper we analyze the hydrological characteristics West Liaohe River plain and establish the optimal operation model for water resources based on river desertification control.
2.1 Water system of the West Liaohe River plain
The West Liaohe River Plain is formed by alluvial deposits of the West Liaohe River and its main tributaries. West Liaohe River Basin area is 5.2×104 km2. The main rivers of the river system include the lower reach of the Hongshan Reservoir in the Laoha River, the lower reach of the Hairisu Water Diversion Project in the Xilamulun River, the Xinkai River, the main stream of the West Liaohe River, the Jiaolai River and the Wulijimuren River. From late 1990s, the streamway of West Liaohe River Plain frequent drying up. After 2000, due to reduced precipitation, water stored by reservoir, industrial and agricultural water use increased, the trend of streamway dried up aggravated (Wang and Li, 2007).
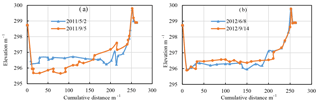
Figure 2Comparison of large cross-section measured before and after flood season at the Taihekou (Xi) station (a: 2011, b: 2012).
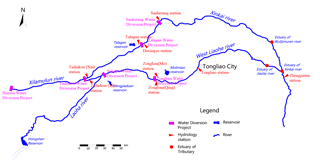
This paper collected nearly 8 years (2006 ∼ 2013) of the West Liaohe River plain river hydrological station (including Taihekou, Daxingye, Talagan, Zongban, Sanhetang, Tongliao, Zhengjiatun) daily flow and sediment data (Fig. 1). The statistical results about runoff of each hydrological station in the West Liaohe River Plain are shown in Table 1.
As shown in Table 1, the annual average runoff of Taihekou (Xi) station is 14 657.3 × 104 m3 and the annual average runoff of Taihekou (Xin) is 3019.9 × 104 m3. The result indicate that only about 17.1 % of total runoff of the Xilamulun River were diverted into the Xinkai River. The annual average runoff of Talagan station on the Xinkai River is 879.7 × 104 m3. Because of seepage loss along the streamway, only about 29.1 % of runoff of Taihekou (Xin) can reach Talagan station. The reach below Daxingye station of the Xinkai River were drying up all the time. From 1998, Hongshan Reservoir, which located in the Laoha River has been in a low water level running, so it did not discharge to downstream and the streamway below Hongsha Reservoir has dried up all the time. The runoff of main stream of the West Liaohe River mainly comes from Taihekou (Xi) station. This runoff diverted into Mengjiaduan Reservoir partly, deducting the seepage along the streamway, the remaining runoff were diverted into Molimiao Reservoir and Yinliaojiqing channel. So the reach below Molimiao Water Diversion Project was dried up all the time. The annual average runoff of Zhengjiatun station is 4901.5 × 104 m3 and the runoff is mainly from Wulijimuren River.
According to the analysis results of hydrological characteristics, the reach of West Liaohe River Plain is divided into intermittent river reach and long dry reach. This paper focuses on the prevention and control of riverbed wind erosion in intermittent river reach.
The river of West Liaohe River Plain has a large amount of sediment. According to the Taihekou (Xi) station monitoring data, the average sediment concentration is 9.07 kg m−3. The sediment concentration increases with the increasing of flow rate. At the same time, the average of median size of riverbed is 0.13 mm, so the change of riverbed erosion and deposition is very severe (Fig. 2).
In the summer flood season in 2011, the maximum flow rate is 585 m3 s−1 at the Taihekou (Xi) hydrological station. After flood season, the riverbed were cut seriously. In the summer flood season in 2012, the maximum flow rate is 151 m3 s−1 at the same cross-section, but the riverbed were deposited seriously. We can come to the conclusion that the longitudinal stability of the riverbed is poor. According to the results of the field investigation, vegetation cover is an effective measure to resist wind erosion in the bare river bed. Due to the longitudinal variation of riverbed, it is difficult to form effective vegetation cover on the riverbed surface. At the drying up time, bare riverbed has become the main source of wind erosion. The optimal water resource operation measures can ensure that the vegetation cover of the river bed is not destroyed frequently by the sediment laden flow.
2.2 Modeling analysis
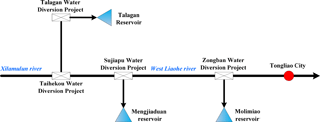
There are three large beside reservoirs (the total capacity of more than 1 × 108 m3) and four large water diversion project in the West Liaohe River plain (Fig. 3). The runoff from upstream is controlled by the water diversion project and diverted into beside reservoir partly. The water resources stored in beside reservoir are used for local industrial and agricultural water supply. Under the premise of ensuring the local industrial and agricultural water supply, whether the water diversion project can be optimized to reduce the water diversion frequency on the riverbed, and then to achieve the purpose of wind erosion control.
2.3 Analysis of water flow evolution considering seepage loss
In the intermittent river reach, a thick unsaturated zone formed beneath the riverbed. When the flow of water through the riverbed, seepage loss is very strong. There are two stages of seepage loss in the intermittent river reach, one is initial infiltration stage and the other is stable infiltration stage. Under the initial infiltration stage, the infiltration rate is large, but the decay rate is faster, and the cumulative infiltration of this stage accounted for a large proportion (Cheng et al., 2015).
Due to the difficulty of accurately dividing the seepage stage, the two stages of seepage loss are considered as a whole. From 2006 to 2013, only 3 years (summer flood season in 2011 and 2012, spring flood season in 2013) that the runoff diverted into Xinkai River by Taihekou Water Diversion Project can reached Talagan Hydrological Station. The daily average flow rate of Taihekou (Xin) station and Talagan station is compared (Fig. 4).
By statistics, the runoff of Talagan station accounted for only 20.38 % of the Taihekou (Xin) station in summer flood season in 2011, and the same ratio is 20.07 % in summer flood season in 2012. This indicates that the water seepage loss from the Taihekou (Xin) station to Talagan station reaches about 80 % of the total runoff. In spring flood season in 2013, the runoff of Talagan station accounted for 49.34 % of the Taihekou (Xin) station, and the seepage loss is relatively small, mainly because of the seasonal frozen soil in the riverbed has not been fully melted.
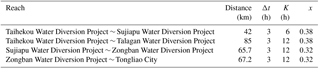
The Muskingum method is used to calculate river water flow evolution in the West Liaohe River plain (Eq. 1). The water flow evolution parameters are the results (Table 2) of the “West Liaohe River flood control planning report” (Northeast investigation and Design Institute of Ministry of water resources, 2005).
where Qup, 1, Qup, 2, Qdown, 1, Qdown, 2 are the inflow of beginning and end period of the upper section, and the outflow of beginning and end period of the down section respectively, m3 s−1. C0, C1, C2 are parameters. K is propagation time of the reach under steady flow, hour. x is the flow proportion factor, in addition to reflect on the role of wedge storage flow, also reflect the storage capacity of the river. Δt is the calculation period, hour.
Considering the optimization calculation is too large, and the degree of concern for water quantity is higher than the flow process, simplified flow evolution and seepage loss coupling and used the comprehensive seepage loss coefficient. However, it is necessary to distinguish between spring flood season and summer flood season, expression is as flow:
where Sf, r is the comprehensive seepage loss coefficient of reach r. The comprehensive loss coefficient can be approximately considered as linear correlation with the length of the river. Because of the lack of measured hydrological data, the comprehensive loss coefficient of seepage of other reach can be calculated by the correlation between the loss coefficient and the length of the reach which is from Taihekou to Talagan Water Diversion Project:
where Lr is the length of reach r, km.
To verify the comprehensive river seepage loss coefficient, the measured data of Daxingye station and Sanhetang station on the Xinkai River were selected from 1999 to 2000. The reach length is 36.7 km between the two hydrological stations. The comprehensive loss coefficients of spring and summer flood season were 0.78 and 0.65 respectively using Eq. (3). However, the measured values were 0.72 and 0.69 respectively, so the calculated result is close to the measured value. It is proved that the assumption of linear correlation between the loss coefficient and the length of the reach is reasonable. It is needed to be explained that the comprehensive seepage loss coefficient of reach was obtained under the condition that the river dried up for a long period previously. So the river water conditions will have a certain impact on the coefficient.
2.4 Hydraulic connection
The distribution of river flow is controlled by water diversion project. Through the water diversion project, river flow can be diverted into beside reservoir or lower reach. The hydraulic connections which take water diversion project as a node are described below.
where QTaihekou_in, QTaihekou_out, QTaihekou_diversion are inflow, outflow and diversion flow of the Taihekou Water Diversion Project respectively, m3 s−1.
where QTalagan_in, QTalagan_out, QTalagan_diversion are inflow, outflow and diversion flow of the Talagan Water Diversion Project respectively, m3 s−1. QTaihekou_diversion_evolution is the diversion flow rate that evolved from Taihekou to Talagan Water Diversion Project, m3 s−1.
where QSujiapu_in, QSujiapu_out, QSujiapu_diversion are inflow, out flow and diversion flow of Sujiapu Water Diversion Project respectively, ,m3 s−1. QTaihekou_out_evolution is the outflow rate that evolved from Taihekou to Sujiapu Water Diversion Project, m3 s−1.
where QZongban_in, QZongban_out, QZongban_diversion are inflow, outflow and diversion flow of Zongban Water Diversion Project, m3 s−1. QSujiapu_out_evolution is the outflow rate that evolved from Sujiapu to Zongban Water Diversion Project, m3 s−1.
According to the analysis results of hydraulic system, the system is a mixed type system and the hydraulic connection between upstream and downstream is closely. The distribution of water resources were controlled by four water diversion projects, so the dimension of the system space is four dimensional. Based on the results of hydrological statistical analysis, the Water Diversion Project of Talagan and Zongban had no outflow in recent 8 years (from 2006 to 2013). So we use regular operation mode for the Water Diversion Projects of Talagan and Zongban, and the two Water Diversion Projects no longer participate in optimal operation. Specific to Zongban Water Diversion Project as an example:
- 1.
When QZongban_in>QZongban_diversion_max, then QZongban_diversion=QZongban_diversion_max, and then .
- 2.
When QZongban_in≤QZongban_diversion_max, then QZongban_diversion=QZongban_in, and QZongban_out=0. Where QZongban_diversion_max is the maximum capacity of diversion flow of Zongban Water Diversion Project, m3 s−1.
After using regular operation mode for the Water Diversion Projects of Talagan and Zongban, the four dimensional optimization problem can be reduced to two dimensional optimization problem, and only the Water Diversion Projects of Taihekou and Sujiapu can be seen as targets of the optimal operation. The outflow and diversion flow are optional state variables for every water diversion project. In order to meet the threshold setting and the realization of the target, the diversion flow is chosen as the state variable in Taihekou Water Diversion Project and the outflow is chosen as state variable in Sujiapu Water Diversion Project.
3.1 Objective function
The inflow of Taihekou Water Diversion Project is mainly concentrated in the spring flood season (from 10 March to 20 April) and summer flood season (from 25 June to 20 August). Other times the riverbed is in the drying up state. The maximum inflow were 147 and 1074 m3 s−1 of the Taihekou Water Diversion Project in spring flood season and summer flood season respectively.
Because the water diversion project has no capacity for runoff regulation, the inflow either diverted into beside reservoir or discharged into lower reach. Due to the extreme shortage of local water resources, the water eventually was diverted into beside reservoir regardless of diversion flow or outflow. Therefore, it is a prerequisite to optimize the operation of water resources to meet the requirements of the local industry and agriculture. Based on the prevention and control of wind erosion of riverbed, it is beneficial that the river discharge or dry up for a long time. If the upstream flow is less, the flow is firstly diverted into nearest beside reservoir and reduce interference on the downstream of the river. If the upstream flow is larger, the flow is diverted into long distance beside reservoir preferentially, concentrated flow and reduce the frequency of water through of riverbed. Therefore, as the objective function, it is needed to consider diversion flow or outflow and river length. Specific expressions are as follows:
where obj is objective function; j is the Number of reservoir; objj is objective function value of j reservoir water storage. Lj is the distance from Taihekou Water Diversion Project to j reservoir, km; Vj, cap is utilizable capacity of j reservoir, 104 m3; Ij is the volume of water that had diverted into j reservoir in calculation period, 104 m3; P is penalty coefficient; Qj, t is the flow rate that diverted into j reservoir. is the maximum flow rate of flood, m3 s−1; Qj, thr is the lower threshold of flow rate that diverted into j reservoir, m3 s−1; sign is indicator of status.
The objective function includes two aspects: (1) the objection of water volume that diverted into beside reservoir and (2) the objection of wind erosion prevention and control of riverbed. The objective function is essentially a function of the reach length (Lj) and the amount of water diverted into beside reservoir (Ij). is a dimensionless variable coefficient, when the amount of water diverted into j reservoir increases, the coefficient becomes smaller. Through the objective function can ensure the amount of water diverted into beside reservoir, and thus guarantee the local industrial and agricultural water supply.
The lower threshold flow is one of the key variables of the objective function. Through this variable, it can avoid the interference of high-frequency of small flow rate to the lower reach. To obtain the lower threshold flow, we can use two methods of optimization and simulation. If the optimization method is used to solve the problem, it is necessary to add two dimension on the basis of the original two dimensional optimization problem; and the use of simulation method to solve, we can learn from the operation experience, given a reasonable lower threshold flow. This paper uses simulation method to obtain the lower threshold of diversion flow of Taihekou Water Diversion Project and outflow of Sujiapu Water Diversion Project respectively. The lower threshold flow setting is directly related to the volume of diversion flow of Talagan and Zongban Water Diversion Project. The optimal value of the lower threshold of the diversion flow is based on the measured water diversion of the Talagan and Zongban Water Diversion Project.
In this paper, the problem of optimal flood control is not studied, and the flood discharge of each river is given in the form of constraint.
3.2 Constraints
3.2.1 Water balance of reservoir
where Vj, t and are water storage at the beginning and end of the period t respectively in reservoir j; Ij, t is runoff of reservoir j in period t; Wj, t is water supply of reservoir j in period t; Ej, t is the loss of evaporation and seepage of j reservoir in period t; Aj, t is surplus water of j reservoir in period t.
3.2.2 Constraint of discharge capacity
where Qr, t is the flow rate of reach r in period t, m3 s−1; Qr, max is the discharge capacity of reach r, m3 s−1;
3.2.3 Constraint of upper bound of reservoir water storage
where Vj is water storage of reservoir j in period t, 104 m3; Vj, nor is upper bound of water storage of reservoirj, 104 m3.
3.3 Search method
3.3.1 Constraint handling method
In the process of water resources optimal operation, the constrained optimization problem is transformed into unconstrained optimization problem by penalty function generally. In this paper, the discharge capacity and the upper bound of reservoir water storage are all mandatory constraint. When the variables violate the constraints, the penalty term is added on the basis of the results of the original objective function. Specific expressions are as follows:
where F1 and F2 are the penalty coefficient of the flow rate and water storage respectively; obj′ is the objective function value that is added by the penalty value.
3.3.2 Solving process
Water diversion project itself does not have the ability to regulate runoff, only transform the inflow into diversion flow or outflow. Importantly there is a time effect of water flow evolution, that is, there is post-efficiency, which is essentially different from reservoirs. Therefore, the solution method of the optimal operation of the water diversion project group is quite different from the reservoir group.
In order to simplify the problem solving, multi-dimensional optimization problems are usually transformed into one-dimensional optimization problems, such as DPSA (Dynamic Programming Successive Approximation) in dynamic planning (Opan, 2010; Yi et al., 2003). Multi-stage optimization can also be translated into a single two-stage optimization problem, such as POA (Progressive Optimality Algorithm) in dynamic plan (Liu et al., 2011; Guo et al., 2011). If DPSA and POA are combined (DPSA-POA), the multi-dimensional and multi-stage optimization problems can be transformed into one-dimensional and two-stage optimization problems (Bai et al., 2015; Zhang et al., 2016), and the difficulty of solving optimization problems reduced greatly, at the same time, the problem of post-efficiency can be solved effectively.
To solve the problem of the water resources optimal operation based on riverbed wind erosion control in West Liaohe River plain, and improve computational efficiency, this paper presents a “multi-core parallel solution algorithm for optimal operation of water diversion project group”.
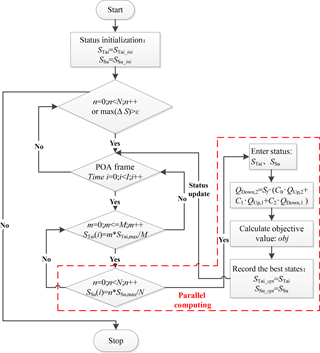
From the above analysis, we can see that the upper and lower reaches are closely linked to each other of the optimal operation system in this paper, and two independent state variables find the optimal combination of states through the DPSA method under the framework of POA to get the optimal operation scheme. According to the relationship between upstream and downstream, Taihekou Water Diversion Project is the first level, Sujiapu Water Diversion Project is the final level. Under the framework of POA, we only change the state variable of the last stage i at a time, and the first state variable is fixed. The full range of two complete series are brought into the calculation method of objective function. According to the calculation method of water flow evolution, the diversion flow and outflow of each water diversion project are calculated, and then the objective function value is calculated. When the traversal of the final level at time i is completed, the state variable of its parent is changed. When all traversal completed at time i, then , until all the time were completed. The whole process is repeated n times, until the difference between the two calculation results is less than the set threshold, you can stop the calculation. Calculation process is shown in Fig. 5. In the figure, M and K are the number of diverting states of Tahekou and Sujiapu Water Diversion Project, respectively, and their values can be selected comprehensively according to the state change field and the calculation precision.
From the entire calculation process, the calculation is the largest in the final cycle. It is necessary to calculate the evolution of water flow under fixed stages of two water diversion project. It is necessary to calculate the amount of diversion flow and out flow of each water diversion project and calculate the entire objective function value. In this paper, the last stage is changed into parallel computing mode to balance the load of each thread, so as to avoid the cost of thread synchronization at the end of the cycle. The Fork/Join framework is a framework for performing parallel tasks. In the final cycle, each subtask is independent of each other, so the task can be distributed to multiple threads, and the results of multiple subtasks can be combined into a total calculation result.
The performance of parallel algorithm is evaluated by speedup ratio and parallel efficiency (Peng et al., 2014), and the expression is as follows:
where Sp is speedup ratio; Ts is serial computing time consuming; min; Tp is parallel computing time consuming; min; Ep is parallel efficiency; P is processor number.
Taking Taihekou Water Diversion Project daily measured flow from 2006 to 2013 as input condition, on the basis of guaranteeing the total water separation of various reservoirs, avoid the destruction of riverbed vegetation by the frequent overflow of the river through the optimal operation of Taihekou and Sujiapu Water Diversion Project, and achieve the goals of riverbed wind erosion control. The combination of the different thresholds of water diversion at the Taihekou and the Sujiapu Water Diversion Project are analyzed. Take Talagan and Zongban Water Diversion Project measured water diversion volume value as the verification. The results are shown in Table 3.
Table 3Analysis of threshold of diversion flow at Taihekou Water Diversion Project and threshold of outflow at Sujiapu Water Diversion Project. Values in bold indicates that Scheme 2 is the best scheme.
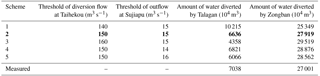
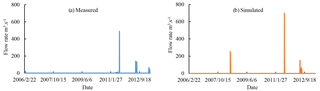
Figure 6Comparison of simulated and measured diversion flow into Xinkai River at Taihekou Water Diversion Project.
It can be seen from the calculation results in the table that the lower threshold of water diversion for Taihekou Water Diversion Project is set to 150 m3 s−1 and the release threshold of Sujiapu Water Diversion Project terminal set to 15 m3 s−1 is more appropriate (Scheme 2 in Table 3). The simulated diversion water volume of the Talagan Water Diversion Project is 6636×104 m3, and the measured value is 7038×104 m3. The simulated diversion water volume of the Zongban Water Diversion Project is 27 919×104 m3, and the measured value is 27 001×104 m3. The simulation results and the measured values are relatively close.
Under scheme 2, Taihekou Water Diversion Project has diverted into Xinkai River for 3 years, summer flood in 2008, summer flood in 2011 and summer flood in 2012 respectively. The number of draining days at Talagan Water Diversion Project is 29 days. In the measured value, Taihekou Water Diversion Project has diverted into Xinkai River for 4 years, spring flood in 2006, summer flood in 2011, summer flood in 2012 and summer flood in 2013 respectively. The number of draining days at Talagan Water Diversion Project is 44 days. The results of the comparison between the calculated and the measured are shown in Fig. 6. In the spring flood season of 2006, the maximum inflow of Taihekou Water Diversion Project was 132 m3 s−1. In the actual operation, the maximum diversion flow into Xinkai River is 19.4 m3 s−1, and the amount of water diverted into Xinkai River is 503×104 m3 in the whole spring flood season. Leakage along the river consumes the vast majority of water. While not meeting the purpose of diversion water storage, the large amount of sediment carried by the water current also undermined the growth environment of the bed vegetation. After the optimal operation, only when the inflow of Tahekou Water Diversion Project exceeds the set threshold, it will be diverted into Xinkai River. Taking the summer flood season in 2011 as an example, the maximum of inflow of the Taihekou Water Diversion Project is 1074 m3 s−1, and the total flood runoff in this session is 25 320×104 m3. After optimization calculation, the maximum flow diverted into Xinkai River is 698 m3 s−1 (the measured value is 489 m3 s−1), and the amount of water diverted into Xinkai River is 11 900×104 m3 (measured value is 8655×104 m3). The maximum diversion flow and total amount of diversion water have been greatly increased compared with the measured values.
Under scheme 2, Zongban Water Diversion Project has inflow water for 7 years and the total number of inflow days is 176 days. In the measured values, Zongban Water Diversion Project also has inflow water for 7 years and the total number of inflow days is 200 days.
The results of comparison between the optimized operation and the measured data show that the number of years of water passing through the Zongban Water Diversion Project is the same with the measured value and the number of years that the Taihekou Water Diversion Project diverted into Xinkai River decreased by 1 year after the optimal operation is implemented. For the number of draining days, the number of draining days at Talagan and Zongban Water Diversion Project decreased to some extent contrast with the measured value, but the reduction in the number of draining days at Talagan Water Diversion Project was relatively large.
Through the above analysis we can see that the setting of the lower threshold of diversion flow and the amount of water diverted into the reservoir are conflicting. On the basis of guaranteeing the amount of water diverted into the reservoir, setting a reasonable lower threshold of flow diverted into the new Xinkai River of Taihekou Water Diversion Project and lower threshold of outflow of the Sujiapu Water Diversion Project can make the Xinkai River from Taihekou to Talagan Water Diversion Project (river length of 85 km) and the West Liaohe River from Sujiapu to Zongban Water Diversion Project (length of 65.7 km) through a larger water flow and control the lower flow in the reach. Reduce the frequency of river flow as much as possible, and reduce the frequent damage of water flow to the vegetation cover of the riverbed. The goal of water resources optimization of West Liaohe River Plain based on the prevention and control wind erosion of riverbed has been achieved.
By optimizing the operation, we can summarize the following rules: (1) When the inflow of Tahekou Water Diversion Project is greater than or equal to 150 m3 s−1, the Xinkai River floodgate is opened to preferentially divert the water into Xinkai River, and more water from the same flood can be diverted into the Xinkai River. (2) When the inflow of Tahekou Water Diversion Project is less than 150 m3 s−1, and the flow rate is less than 15 m3 s−1 after it evolves to Sujiapu Water Diversion Project, it should be diverted into Mengjiaduan reservoir as far as possible. When the inflow of Sujiapu Water Diversion Project is greater than or equal to 15 m3 s−1, give priority to the downstream drainage.
The optimized operation solution test environment is a notebook computer. CPU type is CORE i7, dual-core, 4G memory. After calculation, the serial algorithm takes 14.61 min and the parallel algorithm takes 9.66 min. The speed ratio of the parallel computation is 1.51, and the parallel efficiency is 0.76. It can be seen that the parallel computation of multi core shortens the time consuming and improves the computational efficiency.
- 1.
According to the measured data and actual operation, the West Liaohe River Plain water conservancy project system is simplified to be operation system that is composed of the four water diversion project and three reservoirs. On the basis of this, through the rules and regulations of Talagan and Zongban Water Diversion Projection, the four-dimensional optimization problem is further reduced to a two-dimensional optimization problem.
- 2.
An optimal water resources operation model of West Liaohe River Plain based on the prevention and control of wind erosion of riverbed was established. The model objective function involves the factors such as the amount of water diverted into the reservoir, the length of the river reach and the lower threshold of the flow rate, and on the basis of ensuring the requirements of water diversion in each reservoir, make the river flow through the reach in a short period of time and avoid the destruction of vegetation above the riverbed by the frequent overflow of the river.
- 3.
Proposed a multi-core parallel solution method of water resources optimal operation in West Liaohe River Plain. Find the optimal combination of states by DPSA method under the framework of POA and adopting the Fork/Join mode design parallel computing algorithm in OpenPM programming model, we proposed the calculation flow.
- 4.
The calculation results show that on the basis of ensuring the demand of water diversion into Talagan and Molimiao reservoirs, the threshold of diversion flow from Taihekou Water Diversion Project to Xinkai River is 150 m3 s−1, while the threshold of outflow of the Sujiapu Water Diversion Project is 15 m3 s−1. The optimal operation effectively reduced the water diversion frequency in the Xinkai River reach from Taihekou Water Diversion Project to Talagan Water Diversion Project. Using parallel algorithms, speedup and parallel efficiencies were 1.51 and 0.76, respectively, and computational efficiency improved significantly.
- 5.
The research results of this paper show that it is feasible to achieve the prevention and control of wind erosion of riverbed in the intermittent over-water reach of West Liaohe River Plain through the optimized water resources operation.
The hydrological data used in this study all come from the hydrologic Yearbook (Hydrology data of Liaohe River Basin). According to the People's Republic of China hydrological regulations, hydrological data are not allowed to be made public.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Innovative water resources management – understanding and balancing interactions between humankind and nature”. It is a result of the 8th International Water Resources Management Conference of ICWRS, Beijing, China, 13–15 June 2018.
The study is financially supported by the National Non-Profit Research
Program of China (No.201401015).
Edited by: Depeng Zuo
Reviewed by: two anonymous referee
Bagnold, R. A.: The physics of blown sand and desert dunes, Methuen, London, 265 pp., 1941.
Bai, T., Chang, J., Chang, F., Huang, Q., Wang, Y., and Chen, G.: Synergistic gains from the multi-objective optimal operation of cascade reservoirs in the Upper Yellow River basin, J. Hydrol., 523, 758–767, https://doi.org/10.1016/j.jhydrol.2015.02.007, 2015.
Bao, A., Mu, G., Zhang, Y., Feng, X., Chang, C., and Yin, X.: Estimation of the rational water area for controlling wind erosion in the dried-up basin of the Ebinur Lake and its effect detection, Chinese Sci. Bull., 51, 68–74, https://doi.org/10.1007/s11434-006-8209-9, 2006.
Cheng, L., Wang, Z., Hu, S., Wang, Y., Jin, J., and Zhou, Y.: Flood routing model incorporating intensive streambed infiltration, Sci. China Earth Sci., 58, 718–726, https://doi.org/10.1007/s11430-014-5018-x, 2015.
Englehorn, C. L., Zingg, A. W., and Woodruff, N. P.: The effects of plant residue cover and cold structure on soil losses by wind, Soil Sci. Soc. Am. J., 16, 29–33, https://doi.org/10.2136/sssaj1952.03615995001600010010x, 1952.
Fu, G. and Chen, S.: Water crisis in the Yellow River: facts, reasons, impacts, and countermeasures, Water Practice and Technology, 1, 1–8, https://doi.org/10.2166/WPT.2006028, 2006.
Gao, Y.: Analysis of reasons for the Yellow River's dry-up and its eco-environmental impacts, J. Environ. Sci., 10, 357–364, 1998.
Guo, S., Chen, J., Li, Y., Liu, P., and Li, T.: Joint operation of the multi-reservoir system of the Three Gorges and the Qingjiang cascade reservoirs, Energies, 4, 1036–1050, https://doi.org/10.3390/en4071036, 2011.
Jia, H., Wang, G., Guo, L., Zhuang, J., and Tang, L.: Wind erosion control utilizing standing corn residue in Northeast China, Soil Till. Res., 153, 112–119, https://doi.org/10.1016/j.still.2015.05.009, 2015.
Lal, R.: Soil degradation by erosion, Land Degrad. Dev., 12, 519–539, https://doi.org/10.1002/ldr.472, 2001.
Lee, H. N., Tanaka, T., Chiba, M., and Igarashi, Y.: Long range transport of Asian dust from dust storm and its impact on Japan, Water, Air, & Soil Pollution: Focus, 3, 231–243, https://doi.org/10.1023/A:1023254910362, 2003.
Liu, X., Guo, S., Liu, P., Chen, L., and Li, X.: Deriving Optimal Refill Rules for Multi-Purpose Reservoir Operation, Water Resour. Manag., 25, 431–448, https://doi.org/10.1007/s11269-010-9707-8, 2011.
Northeast investigation and Design Institute of Ministry of water resources: West Liaohe River flood control planning report, Changchun, Report No.: 900-CH7-13, 50 pp., 2005.
Opan, M.: Irrigation-energy management using a DPSA-based optimization model in the Ceyhan Basin of Turkey, J. Hydrol., 385, 353–360, 2010.
Peng, A.-B., Peng, Y., and Zhou, H.,: Multi-core parallel computation for deriving joint operating rule curves in multi-reservoir system under the condition of inter-basin water transfer, J. Hydraul. Eng., 45, 1284–1292, https://doi.org/10.13243/j.cnki.slxb.2014.11.003, 2014.
Shi, H., Li, T., Wang, K., Zhang, A., Wang, G., and Fu, X.: Physically based simulation of the streamflow decrease caused by sediment-trapping dams in the middle Yellow River, Hydrol. Process., 30, 783–794, https://doi.org/10.1002/hyp.10649, 2016.
Wang, X. and Li, L.: The drying-up of the West Liaohe River and the countermeasures to the problem, Journal of Arid Land Resources and Environment, 21, 79–83, 2007.
Wilson, R. and Sprengler, J. D.: Particles in our air: concentrations and health effects, Harvard University Press, Cambridge, Mass, 1996.
Yi, J., Labadie, J. W., and Stitt, S.: Dynamic Optimal Unit Commitment and Loading in Hydropower Systems, J. Water Res. Pl., 129, 388–398, https://doi.org/10.1061/(ASCE)0733-9496(2003)129:5(388), 2003.
Zhang, C. L., Zou, X. Y., Dong, G. R., and Lu, Y. Z.: Wind tunnel studies on influences of vegetation on soil wind erosion, J. Soil Water Conserv., 17, 31–33, 2003.
Zhang, W., Liu, P., Chen, X., Wang, L., Ai, X., Feng, M., Liu, D., and Liu, Y.: Optimal operation of multi-reservoir systems considering time-lags of flood Routing, Water Resour. Manag., 30, 523–540, https://doi.org/10.1007/s11269-015-1175-8, 2016.