Estimating lake-water evaporation from data of large-aperture scintillometer in the Badain Jaran Desert, China, with two comparable methods

Accurate quantification of evaporation (E₀) from open water is vital in arid regions for water resource management and planning, especially for lakes in the desert. The scintillometers are increasingly recognized by researchers for their ability to determine sensible (H) and latent heat fluxes (LE) accurately over distances of hundreds of meters to several kilometers, though scintillometers are mainly used to monitor the land surface processes. In this paper, it is installed on both sides of the shore over a lake. Compared to the data of evaporationpan, the scintillometer was successfully applied to Sumu Barun Jaran in Badain Jaran Desert using the classical method and the proposed linearized β method. Due to the difficulty in measuring water surface temperature and the easiness to monitor the water temperature at different depths, it is worth thinking that if is feasible to utilize the shallow water temperature instead of the water surface temperature and how much errors it will cause. Water temperature at 10 and 20 cm depths were used to replace the lakewater surface temperature in the two methods to analyze the changes of sensible and latent heat fluxes in hot and cold seasons at halfhour time scales. Based on the classical method, the values of H were almost barely affected, and the average value of LE using water temperature at 20 cm depth is 0.8–9.5 % smaller than that at 10 cm depth in cold seasons. In hot seasons, compared to the results at 10 cm depth, the average value of H increased by 20–30 %, and LE decreased by about 20 % at 20 cm depth. In the proposed linearized β method of scintillometer, only the slope of the saturation pressure curve (Δ) is related to the water surface temperature, which was estimated using available equations of saturated vapor pressure versus temperature of the air. Compared to the values of estimated by the air temperature, while the water surface temperature are replaced by water temperature at 10 and 20 cm depths, in different seasons, the errors of 2–25 % in Δ were caused. Thus was calculated by the original equation in the proposed linearized β method of scintillometer. Interestingly, the water temperature at 10 and 20 cm depths had little effect on H, LE (E₀) in different seasons. The reason is that the drying power of the air (E_A) accounted for about 85 % of the evaporation (i.e. the changes of Δ have only about 3 % impact on evaporation), which indicated that the driving force from unsaturated to saturated vapor pressure at 2 m height (i.e. the aerodynamic portion) has the main role on evaporation. Therefore, the proposed linearized β method of scintillometer is recommended to quantify the H, LE (E₀) over open water, especially when the water surface temperature cannot be accurately measured.

1 Introduction

Accurate quantification of evaporation from water body has always been crucial for water resources use and management reasonably, especially in arid regions (Kustas et al., 2000; Bou-Zeid, 2002; Vercauteren et al., 2009; Mcjannet et al., 2011; Mcgloin et al., 2014). Traditionally, evaporation in open water bodies is directly measured by evaporationpan or indirectly calculated by simple aerodynamic approaches using meteorological measurements. The assumptions made by these methods may usually lead to large errors in evaporation calculation. In the last two decades, better technical methods and equipment such as eddy covariance has been developed to estimate the evaporation of open water bodies directly, whose reliability has also been verified by a large number of researches in all sizes about water body (Blanken et al., 2000; Liu et al., 2009; Nordbo et al., 2011; Mcgloin et al., 2014). Due to the limitation in space in evaporation estimation of eddy covariance method, in recent years, scintillometer technology is developed and popular in accurately quantifying the latent heat flux over a greater spatial extent and accounting for possible spatial variability in evaporation resulting from wind, water temperature and depth (Mcjannet et al., 2011). However, Determination of latent heat flux using scintillometry has mainly been limited to studies over vegetation (Guyot et al., 2009). Until recently, Mcjannet et al. (2011) proposed a new approach for obtaining sensible and latent fluxes from a scintillometer deployed over open water. Compared with the results observed by eddy covariance and alternative scintillometer calculation approaches that are commonly used in the literature, the methodology based on linearization of the Bowen ratio was tested and validated.

In the scintillometry calculation, the most important portion is the definition of Bowen ratio (β). Generally, three approaches are used to define βin most researches: the classical method, the β closure method and the proposed linearized β method. Based on the energy balance in the water body studies, however, the heat flux of water body (G) has the significant contribution in the energy balance (Tanny et al., 2008; Vercauteren et al., 2009; Mcgloin et al., 2014; Mcjannet et al., 2011). The measurement of G in water bodies is difficult and leads to large errors easily (Stannard and Rosenberry, 1991). In order to avoid the measuring uncertainty of water surface temperature and the errors produced by different footprints, the slope of the saturation vapor pressure curve (Δ) was estimated from the air temperature using the polynomial equation derived by Lowe (1977) in the proposed linearized β method, however, this also cause some errors in the calculation. The water surface temperature is also needed in the classical method. Due to the difficulty in measuring the water surface temperature and the easiness to monitor the water temperature at different depths, it is worth thinking that if is feasible to utilize the shallow water temperature instead of the water surface temperature and how much errors it will cause.

Figure 1 Location of the study area (a), lakes (b), weather station (c) and scintillometer (d).

In this paper, the scintillometer using the classical method and the proposed linearized β method are applied to Sumu Buran Jaran in Badain Jaran Desert, China, to estimate the evaporation. We also discuss that the effects of water surface temperature replaced by shallow water temperatures at different depths in cold and hot seasons on the scintillometer results.

2 Methods

2.1 Study Area

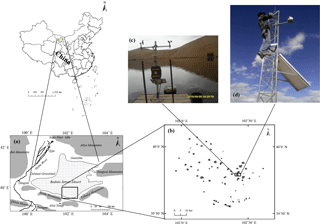
As shown in Fig. 1, the Badain Jaran Desert (39^∘20^′–41^∘30^′ N, 100^∘01^′–103^∘10^′ E) is located in the western Alxa Plateau in Inner Mongolia, China. It is the second largest desert in China covering 4.9 × 10⁴ km² (Wang, 1990). On the north, east and south, the BJD is surrounded by mountains that were mostly formed by granite rocks. The northwest of BJD is Gurinai grassland lying in the downstream area of the Heihe River. Generally, the topography is higher in southeast, lower in northwest. In the desert hinterland, the tall and dense sanddunes and sandhills exist, accounting for as much as 60 % of the desert area, and their relative height are about 200–300 m and up to 500 m. The overall flow of groundwater is from south to north and from east to west, which is consistent with the topography of the desert. Plenty of lakes exist in the BJD, but most of them are smaller than 0.2 km² and shallower than 2 m. More than 65 % of the lakes are saline lakes (TDS > 35 g L⁻¹) and the salinities vary from 1–400 g L⁻¹. In this study, the second largest saline lake-Sumu Barun Jaran was chosen, with the area of 1.24 km² and the maximum depth of 11.1 m. The elevation of the lake is 1150–1200 m.

2.2 Measurements

A large-aperture scintillometer (LAS-BLS450, Scintec AG, Rottenburg, Germany) was installed on both sides of the Sumu Barun Jaran lake consisting of a transmitter (39^∘47${}^{\prime \prime }$44.30${}^{\prime \prime }$ N, 102^∘25^′19.93${}^{\prime \prime }$ E) and a receiver (39^∘46^′51.55${}^{\prime \prime }$ N, 102^∘25^′25.15${}^{\prime \prime }$ E) with 150 mm aperture, an optical wave signal is transmitted to the receiver over a path length (1801 m). The height of the scintillometer to the lake is about 10 m. The near infrared pulse spectrum emitted by the transmitter is 880 nm, and range of the structure parameter of the refractive index of air ($C_n^{\mathrm{2}}$) is from 10⁻¹⁷–10⁻¹⁰ m${}^{-\mathrm{2}/\mathrm{3}}$ reflecting the atmospheric turbulence intensity. The modulation frequency of the scintillometer is 1750 Hz with an averaging period of 30 min. Combined with temperature, relative humidity, wind speed, net radiation and other meteorological data derived from an automatic weather station, the structure parameter of the refractive index of air can be used to estimate the sensible heat flux using Monin-Obukhov similarity theory (Monin and Obukhov, 1954). Once the values of sensible heat flux (H) are obtained, the next step is to calculate the latent heat flux (LE) and evaporation (E₀). The main difference in calculation methods of scintillmeter is the estimation of β. As the water body heat flux (G) is difficult to measure accurately and leads to large errors in results easily, here we do not use the β closure method. However, if we use the shallow water temperature instead of water surface temperature in the β closure method, the heat flux from water surface to the shallow water depth should be estimated when calculating energy balance from net radiation and scintillometer method. The classical method using meteorological data and the proposed linearized β method are studied in this paper. Combined with temperature, relative humidity, wind speed, net radiation and other meteorological data derived from an automatic weather station, the structure parameter of the refractive index of air can be used to estimate the sensible heat flux using Monin-Obukhov similarity theory (Monin and Obukhov, 1954). Once the values of sensible heat flux (H) are obtained, the next step is to calculate the latent heat flux (LE) and evaporation (E₀) on the basis of the β referring to the ratio between the sensible and heat fluxes. Thus, the main difference in calculation methods of scintillmeter is the estimation of β. As the water body heat flux (G) is difficult to measure accurately and leads to large errors in results easily, the classical method using meteorological data and the proposed linearized β method are studied in this paper.

In the classical method, the βis estimated from the other measurements. Assuming that the turbulent transfer coefficients of heat and water vapor are equal above a water body, then we can calculate βusing the measurements of water surface temperature (T_w) and air temperature (T_a) as follows (Penman, 1948):

$$\begin{array}{}\text{(1)}& \mathit{\beta }=\mathit{\gamma }{\displaystyle \frac{T_{\mathrm{w}}-T_{\mathrm{a}}}{e_{\mathrm{w}}^{\ast }-e_{\mathrm{a}}}}\end{array}$$

where $e_{\mathrm{w}}^{\ast }$ is the saturated vapor pressure at T_w.

In the proposed linearized β method, using the method proposed by Vercauteren et al. (2009), evaporation can be estimated by Penman (1948) equation:

$$\begin{array}{}\text{(2)}& E={\displaystyle \frac{\mathrm{\Delta }}{\mathit{\gamma }}}{\displaystyle \frac{H}{L_e}}+E_{\mathrm{A}}\end{array}$$

where Δ is the slope of the saturation pressure curve. L_e is the latent heat of vaporization and γ is the psychometric constant. E_A is the drying power of the air. The calculation procedure shown in Mcjannet et al. (2011) is an iterative process. Starting values of β and Obukhov length (L) is needed to estimate initial values of H and E. From these values a new βcan be calculated which is then fed back through the iterative process to recalculate the structure parameter of the refractive index of air and H. The procedure is run until the solution is stable.

A detailed description of the calculation processes using the two methods to estimate fluxes and evaporation by scintillometer over open water is introduced by Mcjannet et al. (2011).

There are some differences in the calculation procedures used in this study and presented by Mcjannet et al. (2011). Firstly, z₀ was set to 0.0001 m in Mcjannet et al. (2011), however, considering the fluctuations of the lake, in this study it was fixed at 0.0002 m, which is equal to the experiential value of sea. Secondly, the drying power of the air (E_A) was expressed as (PMU, Monteith and Unsworth, 1990, p. 185):

$$\begin{array}{}\text{(3)}& E_{\mathrm{A}}={\displaystyle \frac{\mathit{\rho }{c}_p}{r_{\mathrm{a}}{\mathit{\gamma }}^{\ast }}}\left[e_{\mathrm{s}}\right(T)-e]\end{array}$$

Wherer_a (s m⁻¹) is aerodynamic resistance and e (Pa) is vapor pressure with subscript s denoting the saturation. More detailed calculation equations were presented in Tanny et al. (2011). Thirdly, as we have net radiation data, the net radiation method is used to determine the atmospheric stability, in which that net radiation > 10 W m⁻² is considered as atmospheric instability (Kohsiek et al., 2006). Finally, as we have no data of lake water surface temperature, water temperature at 10 cm depth are used to replace in the classical method.

Figure 2 Dynamic variation (a, c) and comparison (b, d) between the estimated evaporation by scintillometer using the classical method and the proposed linearized β method and observed results by evaporationpan at daily time during 1 July–31 August in 2014.

2.3 Experimental data and Data quality control

Meteorological and scintillometer's data during 12:00 LT (UTC+8) on 26 October 2012 to 20:00 LT on 9 March 2013 and 08:00 LT on 10 May 2013 to 20:00 LT on 26 March 2015 with the interval of 30 min in the daytime are collected in this study. Compared to timezone in Beijing, from 08:00 to 20:00 LT is defined as daytime, and the rest is defined to as nighttime.

Based on Wang et al. (2010), the saturation upper limit of the refractive index of air in Sumu Barun Jaran is set to 1.63 × 10⁻¹³ m${}^{-\mathrm{2}/\mathrm{3}}$, data beyond which are removed. Negative βvalues tended to occurred later in the afternoon, but we did not remove them directly like Mcjannet et al. (2011), and replaced them using positive values.

3 Results analysis

3.1 Reliability verification of scintillometer with two methods

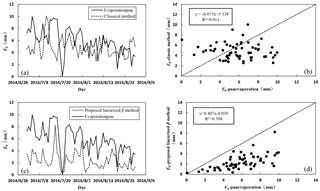
The comparison periods for the proposed linearized β method and the classical method of scintillometer and E601 evaporationpan measurements covered 62 days between 1 July and 31 August 2014 to test the feasibility of scintillometer (Fig. 2). The daily evaporation estimated by scintillometer using two methods are less than those observed from evaporationpan, while their fluctuations are consistent. The evaporation correlation between evaporationpan and scintillometer using the proposed linearized β method (r² = 0.40) is better than that using the classical method (r² = 0.01). The average daily evaporation in July and August measured by pan and estimated by scintillometer using the classical method and the proposed linearized β method is 5.89, 4.90 and 2.36 mm, respectively. Evaporationpan data is 17 and 60 % higher than the corresponding average daily values of scintillometer using the classical method and the proposed linearized β method. That the evaporation calculated by scintillometer using two methods are less than the values observed from evaporationpan has two reasons. One is that the evaporationpan cannot store thermal energy. The other reason is that the data in atmospheric unstable condition in the daytime (i.e. R_n > 10 W m⁻²) are used in the calculation of scintillometer, not all data from 08:00 to 20:00 LT. Moreover, the scintillometer did not record data at some point. These two kinds of data that are not used in the calculation account for 38 % of the total data. Thus, the average daily evaporation in July and August estimated by scintillometer using the classical method and the proposed linearized β method is 6.76 and 3.26 mm, respectively. The average daily evaporation estimated by scintillometer using the classical method and the proposed linearized β method is 15 % higher and 45 % lower than the result (5.89 mm) derived from evaporationpan, respectively. The results derived from the scintillometer using the classical method are closer to the average daily evaporation estimated from E601 pan. The average evaporation estimated by the proposed linearized β method accounts for 48 % of the corresponding average daily value calculated using the classical method. The great difference of evaporation estimated by scintillometer using two methods may be mainly caused by two reasons. One reason is due to the water surface temperature. As the water surface temperature is needed to calculate the β value in the classical method, whereas the water surface temperature here is replaced by the water temperature at 10 cm depth. The other reason is that use of the classical method involves iteratively solving only for L as β is specified from measurements, while both of the L and βin the proposed linearized β method are calculated iteratively until the solution is stable. Although the evaporation estimated by scintillometer and evaporationpan are not exactly the same, they have the similar magnitude and fluctuation trend. Therefore, the scintillometer using two methods are considered to be applied to Sumu Barun Jaran successfully.

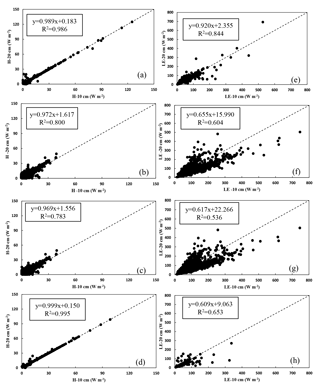
Figure 3 Comparison of the estimated results of H and LE between using water temperature at depths of 10 cm and 20 cm instead of lake water surface temperature in January and February, 2013 (a, e), May and June, 2013 (b, f), July and August, 2014 (c, g), and November and December, 2012 (d, h) with the classical method.

3.2 Shallow water temperature instead of the water surface temperature

Water surface temperature must be employed to estimate evaporation using the classical method in scintillometer procedure. Measuring water surface temperature accurately is so difficult, while measuring water temperature is easy. Therefore, it is worth thinking that if is feasible to utilize the shallow water temperature instead of the water surface temperature and how much errors it will cause.

The water temperature at 20 cm depth is used to replace the lake water surface temperature, compared to the results replaced by the water temperature at 10 cm depth. The cold seasons and hot seasons are defined from November to February, and May to August, respectively.

3.2.1 The classical method

The results using the classical method at halfhour time scale are shown in Fig. 3. Using water temperature at 10 cm depth, the average value of H and LE are 10.83 and 32.37 W m⁻² in January and February, 7.00 and 121.17 W m⁻² in May and June, 6.75 and 119.26 W m⁻² in July and August, and 14.77 and 30.65 W m⁻² in November and December, respectively. From cold to hot seasons, the average value of H decreases by 46 %, and the average value of LE increases by 2.8 times. Replaced by water temperature at 20 cm depth, on average, the value of H and LE are 10.90 and 32.12 W m⁻² in January and February, 8.42 and 95.27 W m⁻² in May and June, 8.09 and 95.81 W m⁻² in July and August, and 14.91 and 27.74 W m⁻² in November and December, respectively. In cold seasons, the average value of H is 36 % lager than that in hot seasons, and LE increases by about 2.2 times. In conclusion, the values of H were almost barely affected, and the average value of LE using water temperature at 20 cm depth is 0.8–9.5 % smaller than that at 10 cm depth in cold seasons. In hot seasons, compared to the results at 10 cm depth, the average value of H increased by 20–30 %, and LE reduced by about 20 % at 20 cm depth. Compared to the results at 10 cm depth, the values of H and LE have greater fluctuation in hot seasons than those in cold seasons.

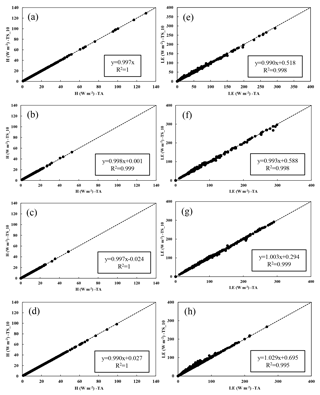
Figure 4 Comparison of the estimated results of H and LE between Δ obtained from the polynomial equation at air temperature and Δ calculated by the original formula at 10 cm depth in January and February, 2013 (a, e), May and June, 2013 (b, f), July and August, 2014 (c, g), and November and December, 2012 (d, h).

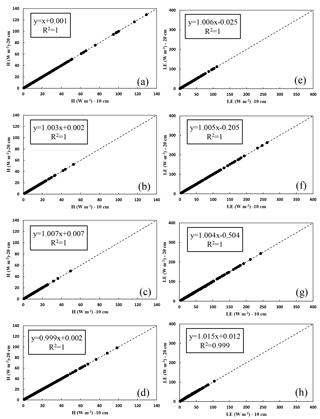
Figure 5 Comparison of the estimated results of H and LE between using water temperature at depth of 10 and 20 cm instead of lake water surface temperature in January and February, 2013 (a, e), May and June, 2013 (b, f), July and August, 2014 (c, g), and November and December, 2012 (d, h) with the proposed linearized β method.

3.2.2 The proposed linearized β method

The proposed linearized β method in scintillometer procedure to calculate evaporation does not need the water surface temperature as only the slope of the saturation vapor pressure curve (Δ) is related to water surface temperature in this approach, which is assumed that Δ can be estimated from the air temperature using the polynomial equation derived by Lowe (1977). However, the assumption also produces 2–25 % errors of Δ in different seasons.

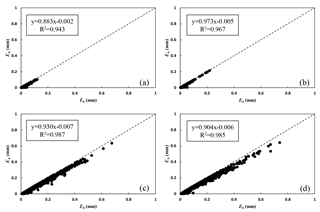
Figure 6 E_A versus E₀ from scintillometer using the proposed linearized β method in January and February, 2013 (a, e), May and June, 2013 (b, f), July and August, 2014 (c, g), and November and December, 2012 (d, h).

In the proposed linearized β method, the results of the Δ estimated by the polynomial equation at air temperature and calculated by the original formula using water temperature at 10 cm depth instead of lake water surface temperature at halfhour time scales are compared (Fig. 4). Using the polynomial equation at air temperature, on average, the value of H and LE are 11.02 and 5.57 W m⁻² in January and February, 3.01 and 80.64 W m⁻² in May and June, 2.91 and 66.96 W m⁻² in July and August, and 14.64 and 7.17 W m⁻² in November and December, respectively. As the lakewater surface temperature are replaced by water temperature at depths of 10 and 20 cm, in both situations, the results of H, LE (E₀) are hardly affected (Figs. 4, 5).

Compared to the values of Δ estimated by the air temperature, while the water surface temperature are replaced by water temperature at 10 and 20 cm depths, in different seasons, the errors of 2–25 % in Δ are caused. However, changes in Δ have little impact on the values of H and LE. Since evaporation is composed of the drying power of the air (E_A) and the expression of Δ based on the Eq. (1) in the Vercauteren et al. (2009), the relationship between E₀ and E_A, shown in Fig. 6. The average value of E₀ and E_A are 0.015 and 0.012 mm in January and February, 0.153 and 0.135 mm in May and June, 0.146 and 0.126 mm in July and August, and 0.024 and 0.018 mm in November and December, respectively. In cold and hot seasons, E_A accounted for about 75 and 87 % of E₀ with good correlation, which indicates that the changes of have an average of 4 and 1 % impact on evaporation, and the driving force from unsaturated to saturated vapor pressure at 2 m height has the main role on evaporation.

4 Conclusions

The scintillometers are increasingly recognized by researchers for their ability to determine sensible (H) and latent heat fluxes (LE) accurately over distances of hundreds of meters to several kilometers, whereas scintillometers are rarely used to estimate the evaporative processes over open water. In this study, the scintillometer was installed on both sides of the shore over a lake for deriving sensible and latent heat fluxes to estimate the evaporation. Compared to the evaporationpan, the scintillometer is successfully applied to Sumu Barun Jaran Lake in Badain Jaran Desert, China using the classical method and the proposed linearized β method.

Under the condition of atmospheric unstability during the daytime, using the classical method, the values of H were almost barely affected by the changes of shallow water temperature in cold seasons, whereas in hot seasons, the H change a lot. In different seasons, variations of shallow water temperature have an influence on LE (E₀) with different extent. Using the proposed linearized β method, shallow water temperature instead of lakewater surface temperature had little effect on H, LE (E₀) in all seasons. The drying power of the air (E_A) accounts for about 85 % of the evaporation, which indicates that the driving force from unsaturated to saturated vapor pressure at 2 m height (i.e. the aerodynamic portion) has the main role on evaporation. Therefore, the proposed linearized β method of scintillometer is recommended to quantify the H, LE (E₀) over open water, especially when the water surface temperature cannot be accurately measured. Although the proposed linearized β method of scintillometer has more advantages than other approach for estimating the H, LE (E₀) over open water, some iterative convergence problems should be concerned.