Guidelines for rainwater harvesting system design and assessment for the city of Johannesburg, South Africa
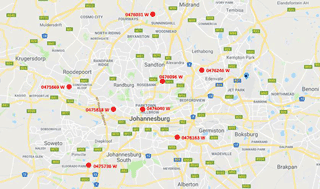
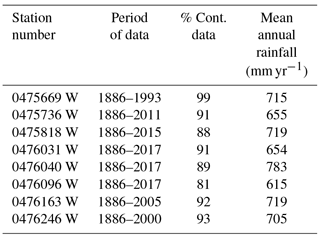
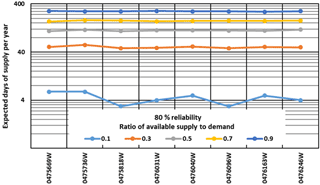
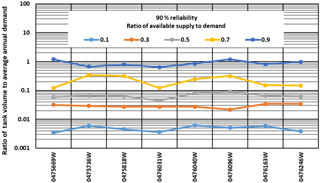
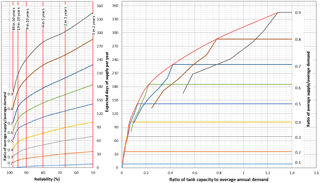
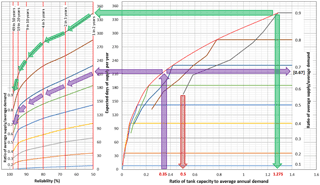
As water demand increases rainwater harvesting (RWH) systems are increasingly being installed for water supply but comprehensive hydrologic design guidelines for RWH do not exist in many parts of the world. The objective of this study was to develop guidelines for the hydrologic design and assessment of rainwater harvesting (RWH) systems in the City of Johannesburg, South Africa. The data for developing the guidelines were mainly obtained from multiple daily simulations of potential RWH systems in the city. The simulations used daily rainfall from 8 stations and demands based on the probable non-potable uses of RWH systems – toilet flushing, air conditioning and irrigation. The guidelines were confined to systems that would typically fill up in the wet season and empty towards the end of the dry season of the same year. Therefore, supply-to-demand ratios ranging from 0.1 to 0.9 were applied. Two generalized design charts of dimensionless relationships were developed. One relates the yield ratio with supply-to-demand ratio and reliability while the other relates the yield ratio with the storage-to-demand ratio and reliability. Reliability was defined as the probability of exceedance of annual yield in order to incorporate the large inter-annual variability of rainfall experienced in the region. The analyses and design of an example RWH system is used to illustrate the application of the design charts.