Trading the Economic Value of Unsatisfied Municipal Water Demand

Modelling and optimization techniques for water resources allocation are proposed to identify the economic value of the unsatisfied municipal water demand against demands emerging from other sectors. While this is always an important step in integrated water resource management perspective, it became crucial for water scarce Countries. In fact, since the competition for the resource is high, they are in crucial need to trade values which will help them in satisfying their policies and needs. In this framework, hydro-economic, social equity and environmental constraints need to be satisfied. In the present study, a hydro-economic decision model based on optimization schemes has been developed for water resources allocation, that enable the evaluation of the economic cost of a deficiency in fulfilling the municipal demand. Moreover, the model enables efficient water resources management, satisfying the demand and proposing additional water resources options. The formulated model is designed to maximize the demand satisfaction and minimize water production cost subject to system priorities, preferences and constraints. The demand priorities are defined based on the effect of demand dissatisfaction, while hydrogeological and physical characteristics of the resources are embedded as constraints in the optimization problem. The application to the City of Amman is presented. Amman is the Capital City of the Hashemite Kingdom of Jordan, a Country located in the south-eastern area of the Mediterranean, on the East Bank of the Jordan River. The main challenge for Jordan, that threat the development and prosperity of all sectors, is the extreme water scarcity. In fact, Jordan is classified as semi-arid to arid region with limited financial resources and unprecedented population growth. While the easy solution directly goes to the simple but expensive approach to cover the demand, case study results show that the proposed model plays a major role in providing directions to decision makers to orient their policies and strategies in order to achieve sustainability of scarce water resources, satisfaction of the minimum required demand as well as financial sustainability. In addition, results map out national needs and priorities that are crucial in understanding and controlling the complexity of Jordan's water sector, mainly for the city of Amman.

1 Introduction

In view of water scarcity, there is a growing strain on surface and groundwater to guarantee socio-economic development and maintain healthy ecosystems. Rapid population growth, climate change, and socio-economic development generate an increasing pressure on water resources to meet domestic, agriculture and industrial water demand and maintain water quality (Loucks and van Beek, 2005). The competition over scarce water resources is increasing. Water demand centres for municipal, industrial, agricultural, hydropower, and environmental uses compete in water stressed countries over conventional (surface and groundwater) as well as unconventional (desalination, brackish and treated wastewater) water. This increase both the importance of reallocating existing water resources more efficiently, and the need for developing new unconventional resources. In view of that, water mangers address the concept of Integrated Water Resource Management (IWRM). Effective water resource management focus on managing different water sources and uses while conserving or improving water quantity and quality. Identification and development of water resources project rely on maximizing net benefit or minimizing costs while considering social, political and environmental impacts. It contains physical, political, and economic measures such as water pricing or marketing policies (Mayer and Muñoz-Hernandez, 2009).

Different approaches combining optimization and simulation tools have been applied on a wide range of water resource management problems. On the basis of objective functions and accompanying constraints, optimization models search for the best solution among the countless options for the infrastructure shape and the water allocation. These models, usually built on economic and/or hydrologic bases, present the advantage of incorporating social value systems in the allocation of the water resource. Other criteria, such as equity, political, or environmental quality can also be used (Loucks and van Beek, 2005); generally speaking, these are more useful if improvement of the system performance is the main goal.

The present contribution exploits the knowledge needed to understand and manage water resources with special emphasis for the capital city of Amman, home for almost forty-two percent of the population of Jordan. The importance of this study derived from the tremendous pressures in service delivery faced by the water uses. This is due to an extraordinary municipal demand growth, linked to the increasing of both the number of refugees entering the Country and the municipal demand, connected with economic development, improvement of living standards and health.

2 The case study

Amman is the capital and the largest city of Jordan. It is the economic, political and cultural centre. Its population is 4 million, 36 % foreign nationals, over an area of 7579 km².

The model case study divides the Amman area in: two domestic demand centres (Amman main and Deep South), one agricultural demand centre, and one industrial demand centre. The model identifies both existing and potential water supply sources from different resources able to satisfy the demand for these centres.

Amman is mainly supplied by renewable groundwater, fossil groundwater, surface water, and treated wastewater. All resources are allowed to supply municipal, agricultural and industrial uses, except treated wastewater that is only used for agriculture and industrial uses. In the actual system, private groundwater wells are owned by the farmer or factory. The Amman main water system is supplied by both internal, including twelve renewable groundwater wellfields, and external water sources imported from other governorates, including 13 sources in addition to the Jafer basin, namely the DISI, through the newly constructed conveyance pipeline on Build Operate and Transfer basis. Deep South water system is supplied by local resources that belong to five wellfields in the Dead Sea basin.

Renewable groundwater resources supply 126 [Mm³ yr⁻¹], fossil groundwater supply 114 [Mm³ yr⁻¹] and surface water supply an average of 135 [Mm³ yr⁻¹]. In the study period (13 years), treated wastewater supplies a total of 296 [Mm³].

3 Methodology

An optimization model is here proposed to allocate water in regions with absolute resource scarcity. It is applied for the period 2018–2030 at Amman governorate level to: maximize social benefits; minimize the dissatisfaction of water demand; minimize the economic cost of water production, that include investment, operation and maintenance, and conveyance costs. Constraints were designed to confine the model according to technical, environmental and institutional aspects and local resource conditions. This analysis extends similar works (Wang et al., 2015; Al-zahrani et al., 2016; Davijani et al., 2016) in which multi-objective optimization models are proposed for water resources allocation considering economic and social objectives. Two objectives are finalized. The first is an economic objective that includes water production and conveyance costs, and agriculture and industrial demand dissatisfaction cost. The second is the dissatisfaction of municipal demand. The model was solved to find the trade-off value assigned to the dissatisfaction of municipal demand objective by founding Pareto front and selecting one of the preferred Pareto optimal choices (Yapo et al., 1998). In the present work, the model is formulated and solved with reference to an annual time-step. Both fixed and variable unit costs related to water production and conveyance are assumed constant in time (no inflation rate), and municipal demand comprises the physical losses.

3.1 Water Demand Prediction

The model considers three kinds of demand points (each demand is associated to a given topographical location):

• a.

  Domestic demand points. These points are mainly in cities and refer to water used for living (drinking, cooking, washing, etc.). This kind of demand is expected to increase in time. In the statement of the problem, it is assumed that such increase is perfectly identified and connected with population growth. Physical losses are considered and estimated using the concept of Non-Revenue Water (NRW), where NRW is assumed to decrease by 1 % each year over the study period. The domestic demand has the highest priority and must be satisfied only by water coming from groundwater, surface water, and desalinated water.

• b.

  Agriculture industrial demand points: it is assumed to be approximately constant over the years and can be satisfied by all water sources.

Each water use is characterized by: (1) the normal demand, representing the target that reflects the amount of water needed to reach economic development and to sustain living standards; (2) the minimum demand, the amount required by a sector that must be satisfied; (3) the maximum demand level (aspiration level – continuous supply). Different kinds of water demands were extracted from utility records. Water demand forecast is focused on the prediction of the normal demand level.

3.2 Allocation model

An optimal water resource allocation model is proposed to achieve the minimum economic cost and maximum social benefit for the capital city of Amman allocating limited water resources under physical and environmental constraints. The optimal water resources allocation model consists of two parts: the objective function, including economic and social aspects, and the constraints, which embed physical, environmental, and social limitations. The allocation model is built on two objectives through:

$$\begin{array}{}\text{(1)}& \mathrm{MIN}=\mathrm{F}\mathrm{1}+\mathrm{DELTA}\cdot \mathrm{F}\mathrm{2}\end{array}$$

where F1 is the economic term and F2 the social term. F1 comprises production and investment costs for the development of potential resources, water conveyance cost, and cost of dissatisfaction of agriculture and industrial demands. The social term expresses the dissatisfaction of the municipal demand, associated to a trade-off factor (delta) that reflects the economic cost of a deficiency in fulfilling the municipal demand.

The model is solved with different values of delta to find the Pareto front. The preferred Pareto optimal point is then selected based on the desired importance for the two objectives.

3.2.1 Available and Potential Resources

The purpose of this section is to present costs and constraints related to the extraction of water from existing and potential resources and to develop a potential resource.

Existing Resources/Renewable Groundwater (RGW)

Let IRGW be the number of wellfields already existing. The cost term to be minimized for this kind of resources is

$$\begin{array}{}\text{(2)}& \mathrm{RGWC}=\sum _{t=\mathrm{1}}^T\sum _{i=\mathrm{1}}^{\mathrm{IRGW}}{K}_i^{\mathrm{RGW}}\cdot y_i^{\mathrm{RGW}}\left(t\right)+c_i^{\mathrm{RGW}}\cdot q_i^{\mathrm{RGW}}\left(t\right)\end{array}$$

where $K_i^{\mathrm{RGW}}$ is the fixed cost [JD] associated with the abstraction from the ith wellfield; $c_i^{\mathrm{RGW}}$ is the variable cost coefficient for water from the ith wellfield [JD Mm⁻³]; $y_i^{\mathrm{RGW}}\left(t\right)$ is a binary variable (BV) that is: 1 if the i-th wellfield is used in year t, and zero otherwise; $q_i^{\mathrm{RGW}}\left(t\right)$ is the water pumped from the ith renewable well field in year t [Mm³ yr⁻¹].

The following constraints must be fulfilled:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{0}\le q_i^{\mathrm{RGW}}\left(t\right)\le q_i^{\mathrm{RGW},\mathrm{MAX}}\\ \text{(3)}& {\displaystyle }& {\displaystyle }i=\mathrm{1},\mathrm{\dots }\text{IRGW and}t=\mathrm{1},\mathrm{2},\mathrm{\dots }T\end{array}$$

Disjunctive constraint:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathit{\mu }\cdot y_i^{\mathrm{RGW}}\left(t\right)-q_i^{\mathrm{RGW}}\left(t\right)\ge \mathrm{0}\\ \text{(4)}& {\displaystyle }& {\displaystyle }i=\mathrm{1},\mathrm{2},\mathrm{\dots }\text{IRGW and}t=\mathrm{1},\mathrm{2},\mathrm{\dots }T\end{array}$$

where $q_i^{\mathrm{RGW},\mathrm{MAX}}$ is the maximum wellfield capacity of ith renewable wellfield [Mm³ yr⁻¹]; its estimation should be based on the groundwater aquifers safe yield; μ is an arbitrary very large number (50×10⁹).

Constraints (4) is introduce to ensure that the fixed cost is paid whenever the wellfield is exploited. Note that there is no necessity of ensuring the opposite as it is automatically ensured by the minimization of the cost function.

Other Existing Resources

The same applies also when considering the cost for water production from existing fossil groundwater (in this case i=1,...IFW), from existing surface water source (in this case i=1,...ISW), and from existing wastewater treatment. One should notice that for the case study under analysis, surface water resource uses are subject to political agreements between Jordan and Israel, that determine abstraction limits for both side, considering the ecosystem demand.

Potential Resources (not yet existing)

Besides optimizing the existing resources, the model suggests when new plants should be built and how “powerful” each new plant should be. The two cost terms are related to the resources exploitation, analogous to the term considered for existing resources, and to construction costs.

Potential Fossil Ground Water (PFW)

Let IPFW be the number of potential wellfields extracting water from the same source – in the case study the potential fossil groundwater resources of Hisban Kafrain, Sheediyya-Al Hasa, and Additional Disi. Then, the decision model minimizes both operational, PFWC1, and investment, PFWC2, costs:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{PFWC}\mathrm{1}=\sum _{t=\mathrm{1}}^T\sum _{i=\mathrm{1}}^{\mathrm{IPFW}}{K}_i^{\mathrm{PFW}}\cdot y_i^{\mathrm{PFW}}\left(t\right)\\ {\displaystyle }& {\displaystyle }\cdot z_i^{\mathrm{PFW}}\left(t\right)+c_i^{\mathrm{PFW}}\\ \text{(5)}& {\displaystyle }& {\displaystyle }\cdot q_i^{\mathrm{PFW}}\left(t\right)\cdot z_i^{\mathrm{PFW}}\left(t\right)\end{array}$$

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{PFWC}\mathrm{2}=\sum _{I=\mathrm{1}}^{\mathrm{IPFW}}\left(\sum _{t=\mathrm{1}}^T{V}_i^{\mathrm{PFW}}\left(t\right)\right)\\ \text{(6)}& {\displaystyle }& {\displaystyle }\cdot \left(B_i^{\mathrm{PFW}}+D_i^{\mathrm{PFW}}\cdot q_i^{\mathrm{PFW},\mathrm{MAX}}\right)\end{array}$$

where $K_i^{\mathrm{PFW}}$ is the fixed cost of abstraction from the ith PFW wellfield [JD]; $y_i^{\mathrm{PFW}}\left(t\right)$ is a binary variable (BV): 1 if the ith PFW wellfield is used in year t, and zero otherwise; $z_i^{\mathrm{PFW}}\left(t\right)$ is a BV: 1 if the i-th PFW wellfield is fully operated at (t), zero otherwise; $c_i^{\mathrm{PFW}}\left(t\right)$ is the variable cost coefficient for quantity of the abstracted PFW from the ith wellfield [JD]; $q_i^{\mathrm{PFW}}\left(t\right)$ is water flow pumped from the ith wellfield [Mm³ yr⁻¹], this constrained to the size of the new plant; $V_i^{\mathrm{PFW}}\left(t\right)$ is BV: 1 if construction the ith wellfield start in year t, and zero otherwise; $q_i^{\mathrm{PFW},\mathrm{MAX}}$ is maximum water flow that maybe pumped from the ith PFW wellfield [Mm³ yr⁻¹]. It is a decision variable that determine the size of the new plant; $D_i^{\mathrm{PFW}}$ is the variable cost coefficient associated to the ith potential wellfield [JD]; $B_i^{\mathrm{PFW}}$ is the fixed cost associated with constructing the planned ith wellfield [JD]; $L_i^{\mathrm{PFW}}$ is the period for constructing PFW wellfield.

The following constraints have to be introduced:

The quantity of water extracted from the ith wellfield should be less than or equal the maximum capacity.

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{0}\le q_i^{\mathrm{PFW}}\left(t\right)\le q_i^{\mathrm{PFW},\mathrm{MAX}}\\ \text{(7)}& {\displaystyle }& {\displaystyle }i=\mathrm{1},\mathrm{\dots }\text{IPFW and}t=\mathrm{1},\mathrm{2}\mathrm{\dots }T\end{array}$$

Disjunctive constraint ensure that the wellfield has been already established when it is exploited:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{z}_i^{\mathrm{PFW}}\left(t\right)=\left\{\begin{array}{l}\mathrm{1}\mathrm{if}{V}_i^{\mathrm{PFW}}\left(t-L_i^{\mathrm{PFW}}\right)=\mathrm{1}\\ \mathrm{Or}\\ z_i^{\mathrm{PFW}}\left(t-\mathrm{1}\right)=\mathrm{1}\\ \mathrm{0}\mathrm{otherwise}\end{array}\right.\\ \text{(8)}& {\displaystyle }& {\displaystyle }i=\mathrm{1},\mathrm{\dots }\text{IPFW and}t\ge L_i^{\mathrm{PFW}}\end{array}$$

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{z}_i^{\mathrm{PFW}}\left(t\right)=\mathrm{0}\\ \text{(9)}& {\displaystyle }& {\displaystyle }i=\mathrm{1},\mathrm{\dots }\text{IPFW and}t\le L_i^{\mathrm{PFW}}\end{array}$$

Imposing fixed exploitation cost constraint if necessary.

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathit{\mu }\cdot y_i^{\mathrm{PFW}}\left(t\right)-q{}_i^{\mathrm{PFW}}\left(t\right)\ge \mathrm{0}\\ \text{(10)}& {\displaystyle }& {\displaystyle }i=\mathrm{1},\mathrm{\dots }\text{IPFW and}t=\mathrm{1},\mathrm{2},\mathrm{\dots }T\end{array}$$

Disjunctive constraint to insure the use of the wellfield when it is build and fully operated.

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathit{\mu }\cdot z{}_i^{\mathrm{PFW}}\left(t\right)-y{}_i^{\mathrm{PFW}}\left(t\right)\ge \mathrm{0}\\ \text{(11)}& {\displaystyle }& {\displaystyle }i=\mathrm{1},\mathrm{\dots }\text{IPFW and}t=\mathrm{1},\mathrm{2},\mathrm{\dots }T\end{array}$$

Preventing multiple start of construction of a wellfield.

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\sum _{t=\mathrm{1}}^T{V}_i^{\mathrm{PFW}}\left(t\right)\le \mathrm{1}\\ \text{(12)}& {\displaystyle }& {\displaystyle }i=\mathrm{1},\mathrm{\dots }\text{IPFW and}t=\mathrm{1},\mathrm{2},\mathrm{\dots }T\end{array}$$

$L_i^{\mathrm{PFW}}$ is the number of time interval for the ith new FW wellfield.

A constraint limiting the size of the plant.

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{q}_i^{\mathrm{PFW},\mathrm{MAX}}\le {\mathrm{MAXSIZE}}^{\mathrm{PFW}}\\ \text{(13)}& {\displaystyle }& {\displaystyle }i=\mathrm{1},\mathrm{\dots }\mathrm{IPFWand}t=\mathrm{1},\mathrm{2},\mathrm{\dots }T\end{array}$$

where MAXSIZE^PFW is the maximum admissible size of the plant in site i; assumed technical known.

Other Potential Resources

The above applies also when considering the cost for building plants and produce water from potential wastewater treatment plants (i=1,...IPWWT), and for the potential desalination plants (i=1,...IDP).

3.2.2 Transmission cost

The transmission cost is dependent on the topology of the transmission network which depend on topography. This require deep knowledge of the topographic characteristic of the region. Simplification of point to point connection costs is used based on the fact that the transmission network is (almost entirely) already existing.

Transmission Cost from Renewable Groundwater (RGW) to Agriculture Demand (AD) Points

Introducing JAD as the number of agriculture demand points (in our model one agriculture centre) and IRGW as the number of renewable groundwater wellfields, then the cost of transmitting water from a renewable groundwater source to an agricultural demand points is provided by

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathrm{TC}}_{\mathrm{AD}}^{\mathrm{RGW}}=\sum _{t=\mathrm{1}}^T\sum _{j=\mathrm{1}}^{\mathrm{JAD}}\sum _{i=\mathrm{1}}^{\mathrm{IRGW}}{\displaystyle \frac{\mathit{\gamma }\cdot q_{ij}^{\mathrm{AD}\mathit{\_}\mathrm{RGW}}\left(t\right){\left(\mathrm{TDH}\right)}_{ij}}{E_{\mathrm{pi}}}}\cdot \\ \text{(14)}& {\displaystyle }& {\displaystyle }{C}_{\mathrm{Ep}}\cdot \mathrm{\Delta }t\cdot y_{ij}^{\mathrm{AD}\mathrm{\_}\mathrm{RGW}}\end{array}$$

where γ is the specific weight of water = [9.81 KN m⁻³ at 20 ^∘C]; $q_{ij}^{\mathrm{AD}\mathrm{\_}\mathrm{RGW}}\left(\mathrm{t}\right)$ is the water flow from the ith RGW wellfield in time interval (t) to jth agriculture demand point expressed [Mm³ yr⁻¹]; TDH_ij is the total dynamic head; H_Stat is the difference in head between suction and discharge sides of pump in the absence of flow; equals difference in elevation of free surfaces of the fluid source and destination; H_f is the head loss; E_pi is pump efficiency; C_Ep is the cost of pumping water from the ith source based on the efficiency of the pump to any demand center point [JD Kwh⁻¹]; $y_{\mathrm{ij}}^{\mathrm{AD}\mathrm{\_}\mathrm{RGW}}$ is a binary parameter with two values, 1 if the H_Stat greater than zero, zero otherwise; L_ij is the distance between the ith RGW wellfield and jth agriculture demand point [m]; The flow that can be conveyed from ith source to the jth demand points is constrained by

$$\begin{array}{}\text{(15)}& {\displaystyle }\le q_{ij}^{\mathrm{AD}\mathrm{\_}\mathrm{RGW}}\left(t\right)\le q_{ij}^{\mathrm{AD}\mathrm{\_}\mathrm{RGW},\mathrm{MAX}}\end{array}$$

where $q_{ij}^{\mathrm{AD}\mathrm{\_}\mathrm{RGW},\mathrm{MAX}}$ is the maximum flow from the ith source to the jth demand point [Mm³ yr⁻¹].

Transmission Cost from Other sources

Similar transmission cost equations and constraints are used for other sources: existing fossil groundwater (i=1,...IFW), existing surface water (i=1,...ISW), existing treated wastewater (i=1,...IWWT), PFG (i=1,...IPFW), potential wastewater treatment plants (i=1,...IPWWT), and potential desalination plants (i=1,...IDP).

Flows summation from all resources to jth agriculture demand points namely FLA_J (t) in year t, is given by:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\sum _{I=\mathrm{0}}^{\mathrm{IRGW}}{q}_{ij}^{\mathrm{AD}\mathrm{\_}\mathrm{RGW}}\left(t\right)+\sum _I^{\mathrm{IFW}}{q}_{ij}^{\mathrm{AD}\mathrm{\_}\mathrm{FW}}\left(t\right)+\sum _{I=\mathrm{1}}^{\mathrm{ISW}}{q}_{ij}^{\mathrm{AD}\mathrm{\_}\mathrm{SW}}\left(t\right)\\ {\displaystyle }& {\displaystyle }+\sum _{I=\mathrm{1}}^{\mathrm{IWWT}}{q}_{ij}^{\mathrm{AD}\mathrm{\_}\mathrm{WWT}}\left(t\right)+\sum _{I=\mathrm{1}}^{\mathrm{IPFW}}{q}_{ij}^{\mathrm{AD}\mathrm{\_}\mathrm{PFW}}\left(t\right)\\ \text{(16)}& {\displaystyle }& {\displaystyle }+\sum _{I=\mathrm{1}}^{\mathrm{IPWWT}}{q}_{ij}^{\mathrm{AD}\mathrm{\_}\mathrm{PWWT}}\left(t\right)+\sum _{I=\mathrm{1}}^{\mathrm{IDP}}{q}_{ij}^{\mathrm{AD}\mathrm{\_}\mathrm{DP}}\left(t\right)={\mathrm{FLA}}_J\left(t\right)\end{array}$$

Transmission Cost-Industrial and Municipal Demand

Transmission cost to industrial and municipal demand points are introduced, with index j ranges from 1 to JID or 1 to JDD (number of industrial and municipal points). FLI_J(t) and FLD_J(t) presents flows summation from all resources to the jth industrial and municipal demand point, excluding treated wastewater.

3.2.3 Constraints over the resource availability

Constraints on resources overall amount are introduced as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\sum _{j=\mathrm{1}}^{\mathrm{JID}}{q}_{ij}^{\mathrm{ID}\mathrm{\_}\mathrm{RGW}}\left(t\right)+\sum _{j=\mathrm{1}}^{\mathrm{JAD}}{q}_{ij}^{\mathrm{AD}\mathrm{\_}\mathrm{RGW}}\left(t\right)+\sum _{j=\mathrm{1}}^{\mathrm{JDD}}{q}_{ij}^{\mathrm{DD}\mathrm{\_}\mathrm{RGW}}\left(t\right)\\ {\displaystyle }& {\displaystyle }\le q_I^{\mathrm{RGW}}\left(t\right)\\ \text{(17)}& {\displaystyle }& {\displaystyle }i=\mathrm{1},\mathrm{\dots }\text{IRGW and}t=\mathrm{0},\mathrm{1},\mathrm{\dots }T\end{array}$$

The above is a constraint for a typical (presently existing) renewable groundwater plant. The same applies for the other sources: existing fossil groundwater (i=1,...IFW); existing surface water (i=1,...ISW); existing wastewater source (i=1,...IWWT); potential FGW (i=1,...IPFW); potential wastewater treatment plants (i=1,...IPWWT); and potential desalination plants (i=1,...IDP).

3.2.4 Dissatisfied Agriculture/Industrial Demand

Dissatisfied agriculture and industrial objective functions are expressed as:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{Min}\sum _{t=\mathrm{0}}^T\sum _{j=\mathrm{1}}^{\mathrm{JID}}{\mathit{ϵ}}_j\mathrm{Max}({\mathrm{ID}}_j\left(t\right)-{\mathrm{FLI}}_j\left(t\right),\mathrm{0})\\ \text{(18)}& {\displaystyle }& {\displaystyle }+\sum _{t=\mathrm{0}}^T\sum _{j=\mathrm{1}}^{\mathrm{JAD}}{\mathit{\theta }}_j\mathrm{Max}({\mathrm{AD}}_j\left(t\right)-{\mathrm{FLA}}_j\left(t\right),\mathrm{0}))\end{array}$$

where ID_j(t),AD_j(t) is the industrial and Agricultural demand [Mm³ yr⁻¹] for the demand centre [JID] and [JAD] at year t respectively; FLI_j(t), FLA_j(t) is the supplied water for industrial and Agricultural uses [Mm³ yr⁻¹] for the demand centre [JID] and [JAD] at year t respectively; ϵ_j,θ_j are the unit costs of unsatisfied industrial and agriculture demand for the demand centre [JID] and [JAD] in [JD Mm⁻³] respectively.

3.2.5 Municipal Demand Dissatisfaction

The unsatisfied municipal demand, is expressed as:

$$\begin{array}{}\text{(19)}& {\displaystyle }{\displaystyle }\mathrm{Min}\sum _{t=\mathrm{0}}^T\sum _{j=\mathrm{1}}^{\mathrm{JDD}}\mathrm{Max}({\mathrm{DD}}_j\left(t\right)-{\mathrm{FLD}}_j\left(t\right),\mathrm{0})\end{array}$$

were DD_j(t), FLD_j(t) are the municipal demand and supplied water [Mm³ yr⁻¹] for the [JDD] centre at year t.

4 Results and Discussion

The present work is focused on trading the economic cost of the service with the municipal water demand satisfaction. Results here presented are based on the following assumptions: (1) municipal water demand includes the physical losses determined by Non-Revenue Water (NRW), which decline 1 % each year starting from the 2017 level of 38 %; (2) population growth rate is 1.7 %; (3) industrial and agricultural demands are assumed constant over the study period; and (4) fixed and variable unit costs do not account for inflation.

Table 1 Pareto optimal selection.

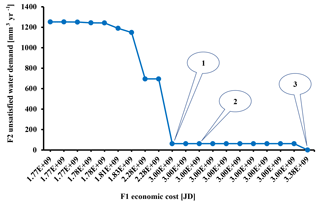
For the given conditions, a trade-off curve can be constructed to describe the relationship between the two objectives (i.e., the economic cost of the service vs. the municipal water demand satisfaction) by changing the cost of unsatisfying the municipal demand by one million cubic meters of water. Figure 1 shows the Pareto front. A negative relation between the dis-satisfaction of the municipal demand and the cost of the service is depicted.

Figure 1 Pareto optimal front.

The choice of the trade-off factor (delta) may take place, theoretically, at any discretization step. Figure 1 depicts also the amount of unsatisfied demand associated with different cost levels.

Selected possible solutions for the allocation problem (see Fig. 1) are represented by:

• Point 1. Unsatisfied municipal demand equal 62.15 [Mm³], and trade-off factor is 1 200 000 [JD];

• Point 2. Un-satisfied municipal demand equal 62.03 [Mm³], and trade-off factor is 2 200 000 [JD];

• Point 3. Un-satisfied municipal demand equal 0, and trade-off factor is 6 090 000 [JD].

Points 1 and 2 satisfy both social and economic objectives but are slightly biased to economic objectives. For Point 3 priority is given to the social objective and the economic objective was ignored. Based on the results described in Fig. 1 and Table 1, the selected Pareto optimal solution is Point 2 with 62.03 [Mm³] unsatisfied municipal demand, now equivalent to 118.1 L c⁻¹ d⁻¹, and an economic cost equal to 3.00 [BJD]. Although Point 3 totally satisfies the normal municipal water demand of 120 [L c⁻¹ d⁻¹], the economic cost is 3.38 [BJD] exceeding Point 2 costs by 377 [MJD]. In other words, at Point 3 a cost of 377 MJD should be paid to increase the water availability by 1.9 L d⁻¹ per person. When compared to Point 1, Point 2 adds 120 000 m³ with a total additional expenditure of 268 000 JD.

5 Conclusions

The estimation of the economic cost associated to a deficiency in fulfilling municipal water demand against demands emerging from other sectors can be obtained through modelling and optimization techniques for water resources allocation under the viewpoint of integrated water resource management (IWRM). This estimation is crucial for water scarce Countries. In fact, in these Countries the high competition for the resource call for the need to trade values which will help them in satisfying their policies and needs.

This model can be replicated and applied to other areas, especially those characterized by an increasing demand-supply deficit or dissatisfaction of municipal water consumers. It will be beneficial and will facilitate their endeavour for sustainable water management.