the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Regionalising MUSLE factors for application to a data-scarce catchment
Andrew Slaughter
Denis Hughes
Sukhmani Mantel
The estimation of soil loss and sediment transport is important for effective management of catchments. A model for semi-arid catchments in southern Africa has been developed; however, simplification of the model parameters and further testing are required. Soil loss is calculated through the Modified Universal Soil Loss Equation (MUSLE). The aims of the current study were to: (1) regionalise the MUSLE erodibility factors and; (2) perform a sensitivity analysis and validate the soil loss outputs against independently-estimated measures. The regionalisation was developed using Geographic Information Systems (GIS) coverages. The model was applied to a high erosion semi-arid region in the Eastern Cape, South Africa. Sensitivity analysis indicated model outputs to be more sensitive to the vegetation cover factor. The simulated soil loss estimates of 40 t ha−1 yr−1 were within the range of estimates by previous studies. The outcome of the present research is a framework for parameter estimation for the MUSLE through regionalisation. This is part of the ongoing development of a model which can estimate soil loss and sediment delivery at broad spatial and temporal scales.
- Article
(2232 KB) - Full-text XML
-
Supplement
(1198 KB) - BibTeX
- EndNote
Soil erosion is a threat to agriculture and the environment, and water-borne sediment disrupts aquatic ecosystem functionality and compromises the quality of water (Msadala et al., 2010). In addition, reservoir sedimentation is a major offsite impact associated with soil erosion (Kusimi et al., 2015). Soil erosion is therefore a critical environmental problem on a global scale, and is also one of the most important environmental problems facing South Africa, particularly in high soil erosion risk areas such the Eastern Cape Province (Le Roux et al., 2008).
Quantifying the rate of soil loss and sediment delivery as well as identifying major contributing factors is important for the effective and sustainable management of catchments. The development of models that estimate erosion and sediment transport is therefore necessary as models enable planners to gain a better understanding of complex natural processes (Xu, 2002) and the data generated can be used to complement scarce observed sedimentation data.
Erosion modelling has commonly been conducted using the Universal Soil Loss Equation (USLE) (Mishra et al., 2006) or models that are based on a similar conceptual understanding (Rabia, 2012). Modifications of the USLE over the years include the Modified USLE (MUSLE) and the Revised USLE (RUSLE) (Mishra et al., 2006). However, most existing erosion models have been developed for European or North American conditions and may not be reliable or appropriate to represent the dynamics of semi-arid catchments in southern Africa. The spatial and temporal variations of erosion processes in semi-arid catchments complicate the process of simplifying patterns of runoff generation and sediment transfer (Hughes, 2008). This relates to catchments in southern Africa that experience extreme hydrological variability, characterised by low annual precipitation and high evaporative losses. Stored sediment loads in these regions can be abruptly flushed out by sporadic high-intensity storms and flash floods.
Internationally-developed models may also require more observed data for model calibration than are typically available for southern African catchments. To address this problem, Bryson (2015) used MUSLE in conjunction with flow input from the Pitman model (Pitman, 1973) to develop a simple erosion and sediment delivery model (WQSED) to effectively represent the sediment dynamics of South African semi-arid catchments. However, the model is characterised by a large number of parameter requirements. In this context, the aim of the current study was to simplify and reduce the parameter requirements and perform a sensitivity analysis, as well as test the erosion and sediment delivery model. This was aimed at improving/developing a model that can provide simulations of soil loss at appropriate spatial and temporal scales. In this regard, Geographic Information Systems (GIS) analyses of readily-available spatial data were explored for regionalising model parameters.
2.1 Study area
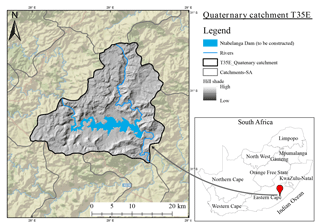
The Tsitsa River catchment is part of the larger Umzimvubu River catchment and is located in the Eastern Cape Province of South Africa. The present study concentrates on the lower quaternary sub catchment of the Tsitsa River catchment, labelled T35E (Fig. 1), which has an area of 492 km2. The quaternary catchment is the principal water management unit in South Africa and denotes a fourth order catchment in a hierarchal classification system in which a primary catchment is the major unit. Although the Umzimvubu River is noted as the largest undeveloped water resource in South Africa (DWA, 2014), plans are underway to construct a dam in T35E.
The catchment varies considerably in geology, with areas of high elevation along the escarpment consisting of basaltic lava from the Drakensberg Formation (Jurassic), underlain by a stratum of Triassic sandstone and mudstone (Le Roux et al., 2015). Soil depth is limited on steep slopes and gradually deepens towards the foot slopes and floodplain areas due to colluvium and alluvial deposits. The thin soils on steeper slopes become highly erodible when vegetation is degraded (Dollar and Rowntree, 1995), and this progressively worsens as livestock graze on the slopes.
The climate of the area is characterised by a distinct seasonality in rainfall and temperatures. Most rainfall (∼ 80 %) occurs during summer (October to March), whereas winter (June to July) is mostly dry. The mean annual rainfall ranges from 625 mm in the low-lying areas to 1415 mm in the mountainous regions (Schulze et al., 2007). Mean monthly temperatures range between 7 ∘C in winter and 19 ∘C in summer, with a high variation during the day (Le Roux et al., 2015).
The Tsitsa River catchment is dominated by the grassland biome, and valley bushveld thrives along river channels in the lower reaches of the catchment (Mucina and Rutherford, 2006). The natural vegetation is largely influenced by altitude and burning (Le Roux et al., 2015); therefore, small patches of Afromontane forest occur along drainage lines and ravines where fire has minimal effect.
2.2 Methodology
The MUSLE was used to estimate soil erosion. The MUSLE is given in the general form of:
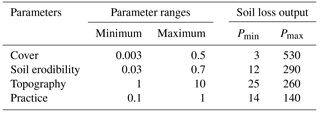
where Sy is sediment yield (t) on a storm basis for the entire catchment, Q is the volume of runoff (m3), qp is the peak flow rate (m3 s−1) and K, L, S, C and P are the soil erodibility (t ha h MJ−1 mm−1), slope length, slope steepness, cover management and soil erosion control practice factors, respectively, similar to the USLE model; parameters a and b are location coefficients. Within the study area for which the equation was developed, the a and b coefficients were 11.8 and 0.56, respectively (Williams and Berndt, 1977). An a priori regionalisation procedure (Kapangaziwiri and Hughes, 2008) was used to estimate K, C and P factors. Regionalisation was adopted to simplify parameter estimation and reduce the user requirements for setting up the model.
In the application of the MUSLE in the present study, the runoff data consists of a monthly discharge record extending from 1920 to 1990. The lack of more recent data records influenced the choice of data that were used within this study. To enable application within MUSLE, the monthly flows from the Pitman Model (Pitman, 1973) were disaggregated to daily. The Pitman Model is one of the most widely used moisture accounting models in southern Africa (Hughes, 2008). Slaughter et al. (2015) present a detailed account of the flow disaggregation method used for the present study. The disaggregated flows were used to obtain the volume (m3) and peak runoff (m3 s−1) that drive the MUSLE model (Bryson, 2015).
A sensitivity analysis was performed to determine the changes in model output that occur when different inputs are used in the model (Loucks and Van Beek, 2005). A simple deterministic sensitivity analysis (Benaman, 2003) was used to measure the response of the model output to changes in values of each factor. Minimum and maximum possible values for the study area were used for each factor. According to Loucks and Van Beek (2005), such a range may reflect differences in model outputs between maximum and minimum values for each factor. The model was initially run using catchment parameter values; these were used as the baseline parameters. The next step included routinely running the model using parameters set to the minimum and maximum values respectively. The process involved testing the parameters one at a time so as to evaluate the variations in model output.
The results of the current study were compared to that by Msadala et al. (2010), who predicted sediment yield for South Africa. It is an improvement to the Rooseboom and Lotriet (1992) erosion prediction map for South Africa, and is the largest recent erosion study and a widely-used reference for soil loss in South African catchments. The Le Roux et al. (2015) sediment yield results for the Mzimvubu River catchment were also used for comparison between model outputs as the Tsitsa River is a tributary of the Mzimvubu catchment. The aforementioned studies used the Soil and Water Assessment Tool (SWAT) (Neitsch et al., 2005) and RUSLE (Renard et al., 1997) models to estimate soil loss. The only limitation is that the outputs of the previous studies are at a coarse spatial scale and provided as mean annual soil loss ranges in t km−2 and t ha−1.
2.3 Determining parameters associated with erodibility
2.3.1 Soil erodibility (K) factor
Soil erodibility refers to the susceptibility of the soil to erosional processes and is dependent on soil characteristics such as structure and texture, which are important determinants of the aggregate soil strength and water infiltration capacity. The K factor is rated on a scale from 0 to 1, with 0 indicating soils with the least susceptibility to erosion, whereas 1 indicates soils which are highly susceptible to soil erosion by water (Schulze et al., 2007).
The soil type distribution for South Africa was obtained from readily-available shapefiles from the South African Atlas of Climatology and Agro-hydrology (Schulze et al., 2007). These data are made available by the Water Research Commission of South Africa (WRC) and contain the distribution of soil types and related K values for soils in South Africa, therefore no empirical soil testing was undertaken. Catchment-specific soil data were extracted from the shapefile by exporting attributes to a Microsoft Excel (2013) spreadsheet. The K factors for various soils were weighted using catchment area to obtain a K factor value that is representative of the entire catchment. This is important because the MUSLE model uses mean values as input for all erodibility parameters.
2.3.2 Topography (LS) factor
The LS factor was determined using an STRM 30 m digital elevation model (DEM) in a GIS environment. The DEM was clipped to the catchment using a mask extraction tool from the ArcGIS toolbox. The DEM was further conditioned to be depressionless using the “fill sink” command to determine the maximum downhill slope and the flow direction (e.g., Jain and Das, 2010). The slope and flow accumulation were derived from the depressionless DEM. The LS factor map was generated in ArcGIS using the raster calculator (Jain and Das, 2010) by using the LS equation:
where FA is the flow accumulation, and α is the slope gradient in degrees. The cell size is the DEM resolution.
2.3.3 Cover (C) factor
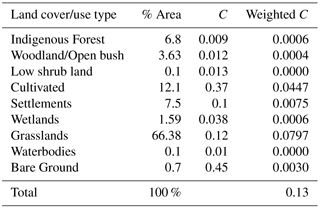
The C factor is a value between 0 and 0.5 that relates to the extent of vegetation cover that protects the soil from erosion in a given catchment (Sadeghi et al., 2013). Cover values closer to 0 indicate dense vegetation cover and reduced erosion output, whereas values close to 0.5 indicate poor vegetation cover. Cover factor values (Table 1) were determined for each land cover type using published guidelines by Wischmeier and Smith (1978), Shinde et al. (2011), Tiruneh and Ayalew (2015), Ranzi et al. (2012) and Jang et al. (2015). Table 1 lists the C factor values for the study area derived used this procedure.
The cover management factor was determined using the National Land Cover data (NLC, 2014). This is the national-scale grid-mapped land cover and land use across South Africa. Catchment-specific cover properties were extracted from the grid by using ArcMap 10.3.1 to clip out catchment-specific data from the NLC map. The attribute table containing land cover categories was exported to a Microsoft Excel (2013) spreadsheet where C factor values published by Wischmeier and Smith (1978) were used to assign C values to respective land cover classes (Table 1). The C values for particular land cover categories were also verified using C values from recent erosion modelling studies, including Shinde et al. (2011), Tiruneh and Ayalew (2015), Ranzi et al. (2012) and Jang et al. (2015). The mean catchment cover factor was determined by weighting the cover factor against respective percentage catchment area for the different land cover categories (Table 1).
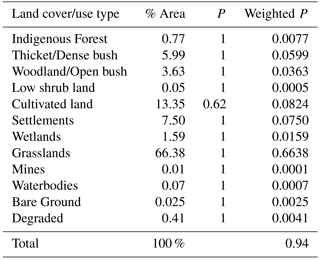
2.3.4 Management practice (P) factor
The management practice factor relates to conservation methods that are implemented to reduce the rate of soil loss from agricultural lands (Tiruneh and Ayalew, 2015). The P factor, which has a value ranging between 0 and 1, refers to management practices that relate to agricultural lands including contour and strip farming. Values closer to 0 indicate good practice and low erosion. The Wischmeier and Smith (1978) table of P values was used to determine P factor values for agricultural land. However, when no conservation was found to be practised, a value of 1 was assigned as the P factor, and all non-agricultural lands were also assigned a P value of 1 if no conservation measure was applied (Tiruneh and Ayalew, 2015; Jang et al., 2015; Luo et al., 2015). Table 2 gives the P factor values for land cover/use types in South Africa.
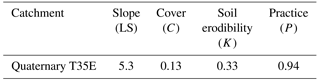
Using land cover/use maps is a relatively easy and efficient method of determining the P factor (Tiruneh and Ayalew, 2015; Jang et al., 2015; Luo et al., 2015). The P factor for the current study was determined by using land use/land cover maps and a slope map to determine the slope categories in which agriculture is practised within the study catchment. Table 3 displays the erodibility values derived for the study site using GIS and the regionalisation procedure.
3.1 Sensitivity analysis
The result of the sensitivity analysis, summarised in Table 4, shows that the model was more sensitive to the parameter relating to vegetation cover (C) as compared to the other parameters. The minimum and maximum ranges for the C parameter gave the lowest and highest model outputs, respectively. The model output associated with the minimum C (Pmin) was > 75 % lower compared to model outputs given by setting the other parameters to minimum values. The same trend was noted at the maximum parameter value where the outputs for the maximum C (Pmax) were > 45 % higher compared to the outputs for other parameters set to their maximums. The model output showed the least sensitivity to the management support practice (P) parameter.
3.2 Model outputs
The simulated results showed that the cumulative amount of soil lost due to erosion in the 492 km2 T35E quaternary catchment is 137 × 106 t over a 70-year period. The mean annual soil loss is 1.96 × 106 t. This translates to approximately 40 t ha−1 yr−1 of soil that is lost from the catchment. The result of the current study falls within the range of the findings of Msadala et al. (2010) who estimated that 26–60 t ha−1 yr−1 is lost from the study area. Le Roux et al. (2015) estimated soil loss for the same area to be 21–50 t ha−1 yr−1. The result indicates a high rate of soil loss that is associated with steep slopes (LS, 5.3) and poor vegetation coverage. The C factor value (0.13) indicates that the catchment is mostly covered by grassland, and field studies conducted in the catchment revealed that the grasslands are mostly degraded by overgrazing and burning.
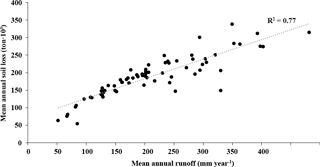
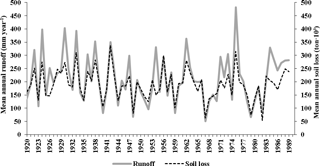
The rate of soil loss correlated well with runoff (Fig. 2). High flows are typically accompanied by increased soil loss. The modelled time series runoff (Fig. 3) shows the typical “flashiness” associated with arid catchments where periods of dryness are followed by large storm events. This triggers rapid erosion, as displayed by the years 1976 and 1977 (Fig. 3). The model output for soil loss also shows the impact of low flows associated with droughts that affected South Africa. The severe drought period of 1980–1983 (Masih et al., 2014) was associated with low flows and reduced soil loss (Fig. 3).
Based on the experience and findings of the present study, regionalisation of the MUSLE inputs using available GIS datasets reduced data requirements of the model. An effective, simple and low input model is essential for southern African catchments with limited observed data. This supports further development of the soil erosion model. Although the use of readily-available datasets to parameterise the model has been shown to yield reasonable results, a disadvantage of this approach is that temporal variations in vegetation cover have not been considered. Accounting for temporal variations in vegetation cover would likely further improve model performance, and should be considered in the future development of the erosion and sediment transport model.
The study examined the use of readily-available GIS coverages to derive values for MUSLE factors. An a priori regionalisation procedure was used and values for the LS, C, P and K factors were estimated based on existing GIS data. The outcome of the application of MUSLE under these conditions was reasonable when compared with previous estimates. A sensitivity analysis conducted within this study showed that the model is 50 % more sensitive to the vegetation C factor compared to the other factors. The consideration of temporal changes in the C factor is therefore important. Model outputs correlated well with runoff; an anticipated outcome as the model is typically driven by runoff. A major limitation within the study was that of data, especially observed data, and validating model simulations using previous estimates was not very reliable, although it provides a starting point in a context of data scarcity. For further model development, it is recommended that observed data are collected to enable model outputs to be compared and validated against actual measurements.
The data used in this study are available at https://doi.org/10.6084/m9.figshare.5606794 (Gwapedza et al., 2017).
The supplement related to this article is available online at: https://doi.org/10.5194/piahs-377-19-2018-supplement.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Water quality and sediment transport issues in surface water”. It is a result of the IAHS Scientific Assembly 2017, Port Elizabeth, South Africa, 10–14 July 2017.
This research was funded by the Water Research Commission (WRC) South
Africa. The data were provided by the Department of Water and Sanitation,
Department of Environment Affairs, USGS explorer and the WRC. They are
thanked for making the GIS data and flow data readily available and free to access.
Edited by: Kate Heal
Reviewed by: Seyed Hamidreza Sadeghi and Ju Qian
Benaman, J.: A Systematic Approach to Uncertainty Analysis for a Distributed Watershed Model, PhD Thesis, School of Civil and Environmental Engineering, Cornell University, Ithaca, NY, 2003.
Bryson, L.: An erosion and sediment delivery model for semi-arid catchments, MS Thesis, Rhodes University, Grahamstown, 2015.
Dollar, E. S. J. and Rowntree, K. M.: Sediment sources, hydro climatic trends and geomorphic response in a mountainous catchment, north Eastern Cape, South Africa, S. Afr. Geogr. J., 77, 21–32, 1995.
DWA: Umzimvubu Water Project, http://www.dwa.gov.za/mzimvubu/documents/announcement/Background Information Document (English).pdf (last access: 8 December 2017), 2014.
Hughes, D. A.: Simulating the hydrology and total dissolved solids (TDS) of an ephemeral river in South Africa for environmental water requirement determinations, River Res. Appl., 24, 1–11, 2008.
Jain, M. K. and Das, D.: Estimation of Sediment Yield and Areas of Soil Erosion and Deposition for Watershed Prioritization using GIS and Remote Sensing, Water Resour. Manage., 24, 2091–2112, 2010.
Jang, C., Shin, Y., Kum, D., Kim, R., Yang, J. E., Kim, S. C., and Jung, Y.: Assessment of soil loss in South Korea based on land-cover type, Stoch. Environ. Res. Risk A., 29, 2127–2141, 2015.
Kapangaziwiri, E., & Hughes, D.: Towards revised physically based parameter estimation methods for the Pitman monthly rainfall-runoff model. Water SA, 34(2), 183–192, 2008.
Kusimi, J. M. andAttua, E. M.: Soil Erosion and Sediment Yield Modelling in the Pra River Basin of Ghana using the Revised Universal Soil Loss Equation (RUSLE), Ghana J. Geogr., 7, 38–57, 2015.
Le Roux, J. J., Morgenthal, T. L., Malherbe, J., Pretorius, D. J., and Sumber, P. D.: Water erosion prediction at a national scale for South Africa, Water SA, 34, 305–314, 2008.
Le Roux, J. J., Barker, C. H., Weepener, H. L., Van den Berg, E. C., and Pretorius, S. N.: Sediment yield modelling in the Umzimvubu river catchment, WRC Report No. 2243/1/15, Water Research Commission, Pretoria, South Africa, 2015.
Loucks, D. P. and Van Beek, E.: Water Resources Systems Planning and Management. An Introduction to Methods, Models and Applications, UNESCO Publishing, Paris, France, 2005.
Luo, Y., Yang, S., Liu, X., Liu, C., Zhang, Y., Zhou, Q., and Dong, G.: Suitability of revision to MUSLE for estimating sediment yield in the Loess Plateau of China, Stoch. Environ. Res. Risk A., 30, 379–394, 2015.
Masih, I., Maskey, S., Mussá, F. E. F., and Trambauer, P.: A review of droughts on the African continent: a geospatial and long-term perspective, Hydrol. Earth Syst. Sci., 18, 3635–3649, https://doi.org/10.5194/hess-18-3635-2014, 2014.
Mishra, S. K., Tyagi, J. V., Singh, V. P., and Singh, R.: SCS-CN-based modelling of sediment yield, J. Hydrol., 324, 301–322, 2006.
Msadala, V., Gibson, L., Le Roux, J. J., Rooseboom, A., and Basson, G. R.: Sediment Yield Prediction for South Africa: 2010 Edition, WRC report 1765/1/10, Water Research Commission, Pretoria, South Africa, 2010.
Mucina, L. and Rutherford, M. C.: The vegetation of South Africa, Lesotho and Swaziland, Strelitzia 19, South African National Biodiversity Institute, Pretoria, South Africa, 2006.
Neitsch, S. L., Arnold, J. G., Kiniry, J. R., and Williams, J. R.: Soil and Water Assessment Tool – Theoretical Documentation, Version 2005, Texas Water Resources Institute, Texas, 2005.
NLC – National Land Cover: 2014 South African National Land-Cover, retrieved from Biodiversity GIS: http://bgis.sanbi.org/DEA_Landcover (last access: 8 December 2017), 2014.
Pitman, W. V.: A Mathematical Model for Generating River Flows from Meteorological Data in South Africa, Report No. 2/73, Hydrological Research Unit, University of the Witwatersrand, Johannesburg, South Africa, 1973.
Rabia, A. H.: Mapping Soil Erosion Risk Using RUSLE, GIS and Remote Sensing Techniques, in: The 4th International Congress of ECSSS, EUROSOIL, 2–6 July 2012, Bari, Italy, 2012.
Ranzi, R., Le, T. H., and Rulli, M. C.: A RUSLE approach to model suspended sediment load in the Lo River (Vietnam): Effects of reservoirs and land use changes, J. Hydrol., 422–423, 17–29, 2012.
Renard, K., Foster, G., Weesies, G., McCool, D., and Yoder, D.: Predicting soil erosion by water: a guide to conservation planning with the Revised Universal Soil Loss Equation (RUSLE), Agricultural Handbook No. 703, United States Department of Agriculture, Washington, D.C., 1997.
Rooseboom, A. and Lotriet, N. H.: The new sediment yield map for southern Africa. Erosion and Sediment Transport Monitoring Programmes in River Basins, in: Proceedings of the IAHS Symposium, 24–28 August 1992, Oslo, Norway, 210 pp., 1992.
Sadeghi, S. H. R., Gholami, L., Khaledi Darvishan, A., and Saeidi, P.: A review of the application of the MUSLE model worldwide, Hydrolog. Sci. J., 59, 365–375, 2013.
Schulze, R. E., Maharaj, M., Warburton, M. L., Gers, C. J., Horan, M. J. C., Kunz, R. P., and Clark, D. J.: South African atlas of climatology and agrohydrology, RSA, WRC Report 1489, Water Research Commission, Pretoria, 2007.
Shinde, V., Sharma, A., Tiwari, K. N., and Singh, M.: Quantitative Determination of Soil Erosion and Prioritization of Micro-Watersheds Using Remote Sensing and GIS, J. Indian Soc. Remote Sens., 39, 181–192, 2011.
Slaughter, A. R., Retief, D. C. H., and Hughes, D. A.: A method to disaggregate monthly flows to daily using daily rainfall observations: model design and testing, J. Hydrol., 4, 153–171, 2015.
Tiruneh, G. and Ayalew, M.: Soil loss estimation using geographical information system in Enfraz watershed for soil conservation planning in Highlands of Ethiopia, Int. J. Agril. Res. Innov. Tech., 5, 21–30, 2015.
Williams, J. R. and Berndt, H. D.: Sediment yield based on watershed hydrology, T. Soc. Agr. Eng., 20, 1100–1104, 1977.
Wischmeier, W. H. and Smith, D. D.: Predicting rainfall erosion losses: a guide to conservation planning, Agricutural Handbook no. 537, United States Department of Agriculture, Washington, D.C., 1978.
Xu, C.: Textbook of Hydrologic Models, in: Vol. 72, Uppsala University Department of Earth Sciences Hydrology, Uppsala, 2002.