A New Software to Model Earth Fissure Caused by Extensive Aquifer Exploitation and its Application to the Guangming Village Case, China

Earth fissures accompanying anthropogenic land subsidence due to excessive aquifer exploitation create significant geohazards in China. Numerical models represent a unique scientific approach to predict the generation and development of earth fissures. However, the common geomechanical simulators fail to reproduce fissure development because they cannot be effectively applied in discontinuous mechanics. An innovative modelling approach developed recently is applied to develop a software to simulate fissure development. The pressure changes are used as forcing factors in a 3D geomechanical model, which combines Finite Elements and Interface Elements to simulate the deformation of the continuous aquifer system and the generation and sliding/opening of earth fissures. The approach has been applied to simulate the earth fissures at Guangming Village in Wuxi, China with land subsidence of more than 1 m caused by the overexploitation of the second confined aquifer. The modelling results highlight that the earth fissures at Guangming Village have been caused by tension and shear stresses. Based on the developed modelling approach and the application case study, a software platform is developed to provide a fast preliminary evaluation of the risk of fissure occurrence associated to land subsidence. The software allows for the simulation of a simplified 2D conceptual geologic model of earth fissures, which can be used to investigate how the main factors controlling the geomechanical response of the aquifer system, such as pressure changes, geometry of aquifer system, geomechanical properties, and depth of bedrock/fault etc.

1 Introduction

Earth fissures accompanying anthropogenic land subsidence due to excessive aquifer exploitation create significant geo-hazards in China (Ye et al., 2016, 2018) and worldwide (Conway, 2016; Peng et al., 2016; Teatini et al., 2018). In China, there are more than 1000 earth fissures identified in densely urbanized regions, specifically Fenwei Basin, North China Plain, and Yangtze River delta (Ye et al., 2016). As an example, the direct and indirect economic loss in Guangming Village of Wuxi city was about USD 20 million in a 1 km² area crossed by two earth fissures (Wang et al., 2016).

Understanding the generation of earth fissures and modelling their occurrence and propagation are important issues to be addressed. Recently, Ye et al. (2018) proposed a novel modelling approach to simulate earth fissure generation and propagation in 3D complex geological settings. A nested two-scale approach associated with an original non-linear elasto-plastic finite element/interface element simulator allows modeling the mechanics of earth fissures. The approach was successfully applied to the Guangming Village in Wuxi, China, where groundwater pumping since 1980 have caused more than 2 m of land subsidence, and two main earth fissures with maximum sliding and opening of 10 to 40 cm. The model outcomes highlight that the main factors contributing to the earth fissure generation include the shallow bedrock with a sharp ridge, the uneven thickness of the sedimentary deposits at the two sides of the bedrock ridge, piezometric decline and the mechanical parameters of the porous material.

The analysis of the failure processes requires advanced numerical modeling capabilities, and the stable and accurate simulation of earth fissure generation and motion is still an open issue. So it is necessary to develop a software platform to model earth fissures caused by extensive aquifer exploitation based on the approach developed by Ye et al. (2018), which can be easily used by experts working on earth fissures. It can provide a fast preliminary evaluation of the risk of fissure occurrence associated to land subsidence and the main factors that typically control the geomechanical response of the aquifer system, including the geometry of bedrock ridge and aquifer system, pressure changes, mechanical parameters and time scale. The software is developed to simulate simplified 2D conceptual geologic models of earth fissures.

The paper is organized as follows. The numerical models are initially introduced. Then, the developed software and its application are presented. In this study, only the simplified aquifer systems, which represent a conceptual schematization of a real-world hydrogeologic setting at Guangming Village in Wuxi, China, are taken into account. For this kind of conceptual model, earth fissures are generated by tensile fractures above a bedrock ridge (Sheng et al., 2003). A summary section closes the paper.

2 Numerical models

Based on the pressure changes are known, modelling of earth fissures is carried out with the use of two separate simulations, which are described as: a geomechanical model for the computation of the displacement and stress fields in a continuous domain, and an earth fissure model that addresses the possible generation and propagation of discontinuities within the porous media (Ye et al., 2018).

2.1 Geomechanical (GM) model

Based on classical poroelastic theory, the equilibrium equations governing the deformation of a mechanically isotropic medium is:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& {\displaystyle \frac{E}{\mathrm{2}}}\left({\displaystyle \frac{\mathrm{1}}{\mathrm{1}-\mathrm{2}v}}{\displaystyle \frac{\partial \mathit{\epsilon }}{\partial x}}+{\mathrm{\nabla }}^{\mathrm{2}}{u}_x\right)={\displaystyle \frac{\partial P}{\partial x}}\\ & {\displaystyle \frac{E}{\mathrm{2}}}\left({\displaystyle \frac{\mathrm{1}}{\mathrm{1}-\mathrm{2}v}}{\displaystyle \frac{\partial \mathit{\epsilon }}{\partial y}}+{\mathrm{\nabla }}^{\mathrm{2}}{u}_y\right)={\displaystyle \frac{\partial P}{\partial y}}\\ & {\displaystyle \frac{E}{\mathrm{2}}}\left({\displaystyle \frac{\mathrm{1}}{\mathrm{1}-\mathrm{2}v}}{\displaystyle \frac{\partial \mathit{\epsilon }}{\partial z}}+{\mathrm{\nabla }}^{\mathrm{2}}{u}_z\right)={\displaystyle \frac{\partial P}{\partial z}}\end{array}\end{array}$$

with E the Young modulus, ν the Poisson ratio, u_x, u_y and u_z the displacement components along the coordinate axes x, y, and z, respectively, ε the volume strain $\mathit{\epsilon }=\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z}$, P the pressure change and ∇² the Laplace operator.

The strain ε and stress σ fields can be obtained from the solution u provided by the GM model using the following relationships:

$$\begin{array}{}\text{(2)}& {\displaystyle }\mathit{\epsilon }=\mathbf{L}u\text{(3)}& {\displaystyle }\mathit{\sigma }={\mathbf{D}}^{-\mathrm{1}}\mathit{\epsilon }\end{array}$$

D is the so-called constitutive matrix. The analysis of the stress and strain fields is important to interpretate the earth fissure development.

2.2 Earth fissure (EF) model

A fissure can be considered as an inner boundary embedded in the continuous body, with a contact condition acting on the opposed surfaces, Γ^top and Γ^bottom , that allows for a relative displacement between corresponding points whenever the stress state violates the classical Mohr-Coulomb failure criterion:

$$\begin{array}{}\text{(4)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{n}}<\mathrm{0}\text{(5)}& {\displaystyle }\mathit{\tau }<{\mathit{\tau }}_{\mathrm{L}}=C-{\mathit{\sigma }}_{\mathrm{n}}\tan \mathit{\phi }\end{array}$$

with σ_n and τ the normal and shear stresses, respectively, acting on the fissure surfaces, τ_L the limit shear strength, ϕ and c the fissure friction angle and cohesion, respectively. Any failure criterion prescribes that the perfect continuity of the displacement across the fissure is preserved if both Eqs. (4) and (5) are satisfied. Otherwise, the contact surfaces are free to develop relative movement u_r:

$$\begin{array}{}\text{(6)}& {\mathit{u}}_{\mathrm{r}}={\mathit{u}}_{\text{bottom}}-{\mathit{u}}_{\text{top}}\end{array}$$

with u_r conventionally defined as the movement u_bottom of Γ^bottom surface with respect to u_top occurring on Γ^top.

The standard Galerkin Finite Element (FE) method is used to solve the 3D geomechanical models with the presence of active/inactive fissure elements. Fissures are discretized by means of Interface Elements (IEs), with shape functions compatible to those of the surrounding solid elements. The displacements at each time step are calculated using the pore pressure gradient presumed as a known body load. Within each iteration of the non-linear Newton scheme, the resulting 3D displacements are used to compute the stress field and the failure criterion is checked on the IEs: if Eqs. (4) and/or (5) are violated, IE opening and sliding may occur and the fissure develops. More details of the models and numerical methods can refer to the paper by Ye et al. (2018).

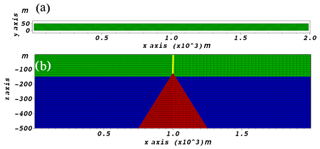
Figure 1 Conceptual schematization of geological setting (a) Plan view of the model grid in this case. (b) Vertical view of the grid. The height of rock ridge (red areas) is 375 m.

Figure 2 Simulated vertical displacements of the aquifer at the (a) 10th and (b) 20th time step.

3 Software and its application

3.1 Software

The software consisting of the GM and EF models, which is developed for simulating the simplified 2D conceptual cross section models of earth fissures at Guangming Village. The software provides a preliminary evaluation of generation and development of the rupture and the main contributing factors leading to the rupture. The software platform allows for changes in the geologic configuration including the depth of the ridge, and the geometry and thickness of the deposits. It also supports modifying other controlling factors such as pressure, mechanical properties of the lithological units, and time scale. The mathematical models for displacement and stress, and earth fissure development, and their corresponding numerical methods of FE and IE are described in Sect. 2. Fortran (2003) is used to code the models. The software includes modules for Input, Geomechanical properties, Fissure conditions, and Output. All the input files are divided into two folders, INPUT and INPUT_IE. If all the input structure allocation completes and the program runs properly, the outcomes are saved in two folders of OUTPUT and OUTPUT_IE.

Figure 3 Ratio of simulated normal stress to the pressure change.

3.2 Application

To demonstrate the applicability of the software, a simplified conceptual schematization of hydrogeologic setting in Guangming Village where the ruptures occur is presented. The domain extends horizontally 2000 m in X direction, 50 m in Y direction and vertically 500 m in Z direction (Fig. 1). A continuous element mesh is discretized by 288 000 tetrahedral elements and 59 326 nodes. In the software, coarse, medium and fine grids are optional. A medium grid is chosen in this application.

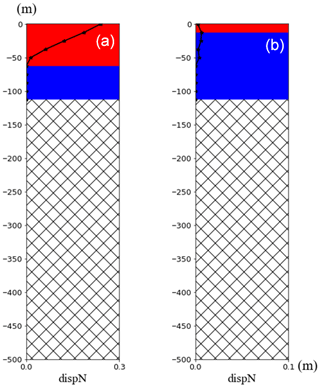
Figure 4 Results of the depth (active in red and inactive in blue) and horizontal displacement (black line) of rupture by IE model at the (a) 10th and (b) 20th time step.

Table 1 Mechanical parameters.

Displacements are prevented along the direction orthogonal to x–z plane. So the software actually simulates the conceptual 2D cross section, although fissure development is 3D by nature. Roller constraints are prescribed on the lateral boundaries with a traction-free top plane and zero displacements on the bottom. The values of mechanical parameters of materials are shown in Table 1. The aquifer (blue layer) is 350 m thick (Fig. 1). In this layer, the pore pressure variation is uniform and varies linearly from 0 to −1 Mpa during a 10 year simulation and recovers inversely to 0 Mpa over the next 10 years. Every year represents a time step, so the whole period contains 20 steps. No pressure change develops in the overlying aquitards (green layer) and in the sharp bedrock ridge (red area). The contact interface (yellow line) has 108 triangular elements which are inserted directly above the tip of the bedrock and reaches the land surface.

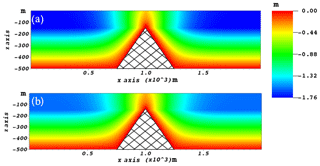
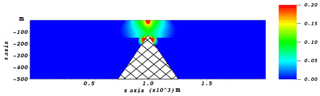
The simulation outcomes demonstrate that when the pressure decreases and the presence of the bedrock ridge induces differential subsidence (Fig. 2). The deformation of the compressing sediment above the ridge causes tension (Fig. 3), which is large enough for the generation of the rupture (Fig. 4a). However, the rupture only remains at a shallow depth as its downward propagation is terminated. Figure 4a shows the maximum fissure opening. The vertical displacement of the sediment and the opening both decrease along with the pressure recovery (Figs. 2b, 4b).

4 Summary

This research aims to develop a software platform to numerically simulate earth fissures caused by groundwater withdrawal in a simplified 3D hydrogeological setting of a cross section with a bedrock ridge. The original mathematical models and numerical formulation developed by Franceschini et al. (2016) and Ye et al. (2018) has been used as the mathematical framework for developing the Fortran codes.

The software allows for changes in the geologic configuration of the system including the depth and shape of the bedrock ridge, the geometry and thickness of the deposits, pressure, mechanical properties of the lithological units, and time scale. A case study of a simplified 2D cross section of the hydrogeological setting at Guangming Village, China, demonstrates that the software can be applied to make a preliminary evaluation of the generation and development of a rupture.