Modelling subsidence due to Holocene soft-sediment deformation in the Netherlands under dynamic water table conditions

Local and regional governments in The Netherlands are increasingly faced with the question how to adjust and optimize groundwater table conditions in urban areas to minimize ongoing subsidence and its consequences. To help addressing this question, a model was developed that includes soft-soil deformation by creep. In this paper, a study is presented in which the model was used to investigate and intercompare the effectiveness of measures that (a) prevent anomalous water table drop during a drought, (b) suppress the seasonal variability of the water table, and (c) involve a permanent rise of the mean water table.

1 Introduction

Urban areas in the western part of The Netherlands commonly show persistent subsidence over multiple decades at rates between 0–10 mm yr⁻¹. At the same time, buildings with a foundation in Pleistocene strata usually show much smaller to negligible subsidence, indicating that the land surface subsidence is mainly caused by slow deformation of clay and peat deposits in the Holocene strata. In contrast to areas with peat oxidation, in urban areas, the persistent nature of the subsidence is thought to be the expression of viscous behaviour (creep) of the subsurface, under periodic addition of fill at the surface to compensate for elevation loss and/or water table lowering. The subsidence causes damage to pipes and cables, damage to buildings and infrastructure without pile foundation, damage to buildings due to decay of wooden pile foundations if the water table is lowered, nuisance flooding, and high maintenance costs of public space functions. Because (ground)water level change can provoke subsidence, and local and regional governments are responsible for groundwater levels in the public space, these governments are faced with the question how to adjust and optimize water table conditions to minimize the subsidence and its consequences. To be able to choose among potential measures, questions they seek answers to include: How much subsidence can be prevented by:

• a.

  preventing excessive water table lowering during an occasional drought;

• b.

  permanent damping of seasonal water table variations;

• c.

  raising of the mean water table?

In this study, modelling was used to address these questions.

2 Methods

2.1 Model formulation

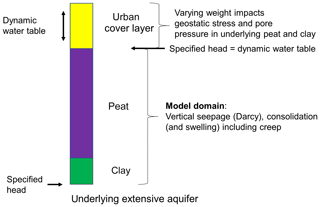
A 1-dimensional mathematical model was built that quantifies the concepts depicted in Fig. 1. The model domain consists of Holocene peat and clay layers. Coupled groundwater flow and deformation (consolidation/swelling) are calculated in these layers, resulting in vertical land movement relative to the underlying Pleistocene aquifer. The natural Holocene stack is overlain by an anthropogenic cover layer (fill), generally consisting of debris and sand that was added in the course of history. The phreatic water table sits within the cover layer and varies in response to weather conditions and human interference. The water table variations directly impact the pore pressure and the geostatic stress in the underlying layers due to the changes in cover layer weight (water content change), and indirectly impact pore pressures by the changing head at the base of the cover layer, which acts as the upper drainage boundary for consolidation and swelling in the peat and clay stack.

Figure 1 Conceptual model.

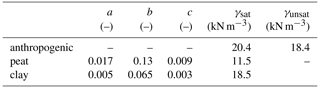
Deformation is calculated employing an isotache-based, viscoelastic compression model that is used in certified geotechnical software for settlement modelling in The Netherlands and other countries. The viscous deformation is referred to as creep. The creep strain in the isotache model is a generalization of, and therefore replaces, the ideal-plastic deformation of Terzaghi's classical elastoplastic compression model. That is, all irreversible deformation in the isotache model is caused by creep. The model uses three compression parameters: swelling constant a, compression constant b, secondary compression constant c; and an (initial) overconsolidation ratio OCR. For a given set of values of the compression parameters, the momentary viscous (creep) time rate of (natural) strain ε_cr is a function of OCR:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}{\mathit{\epsilon }}_{\mathrm{cr}}}{\mathrm{d}t}}={\displaystyle \frac{c}{\mathit{\tau }}}\mathit{\tau }={\mathit{\tau }}_{\mathrm{ref}}{\mathrm{OCR}}^{\frac{b-a}{c}}\end{array}$$

where τ_ref=1 d. τ is intrinsic time, which can be taken as an apparent age of the clay or peat, where young age corresponds to high, and old age to low creep rates. For a comprehensive description of the model, see Den Haan (1994) or Kooi et al. (2018). The model equations are solved with FlexPDE 6.50, a scripted finite element solution environment for partial differential equations.

The model does not account for shrink and swell associated with seasonal desiccation and wetting of clay-rich units in the unsaturated zone (e.g., te Brake et al., 2013).

2.2 Parameter values

Table 1 lists the parameter values that were used for peat, clay and the anthropogenic cover layer in the calculations presented here. Deformation of the cover layer is assumed to be negligible. Hydraulic conductivity of peat and clay was assigned a fixed value of 5 mm d⁻¹. These are representative values that provide a fair impression of the impacts of the water table scenarios. The values of OCR were varied (by specifying τ) in order to vary the background (initial) subsidence rate by creep. A comprehensive sensitivity analysis is beyond the scope of this paper.

Table 1 Parameter values per lithology.

2.3 Model runs

The model was run for the three-layer configuration shown in Fig. 1, with a thickness of 3, 7 and 2 m for the anthropogenic, peat and clay layer, respectively. This layering approximates subsurface conditions in the city of Gouda (Van Laarhoven, 2017). Seasonal water table variations are represented by a sine-function. In reference runs, the mean annual water table is 1 m below land surface and the amplitude 0.5 m. Table 2 summarizes the three modified water table scenarios “dry summer”, “damping”, and “raising” that were used to study their impacts. The magnitude of the applied perturbations is rather large compared to what is generally feasible in practice. This was done to bring out the impacts more clearly.

Table 2 Scenarios for the perturbation applied to the reference ground water table condition.

Note that for “drought” the reference and the scenario should formally be swapped to evaluate the impact of mitigation measures that prevent excessive water table lowering during the drought. In the runs hydraulic head at the base of the clay is kept constant and equal to the mean ground water table. A period of 25 years is simulated.

To study how impacts of water table scenarios vary as a function of the background (or initial) subsidence rate, values of 10, 20 and 100 years were assigned to the initial intrinsic time τ for both the peat and clay layer. These τ values can be converted to corresponding values of OCR using Eq. (1) and the parameter values listed in Table 1.

3 Results

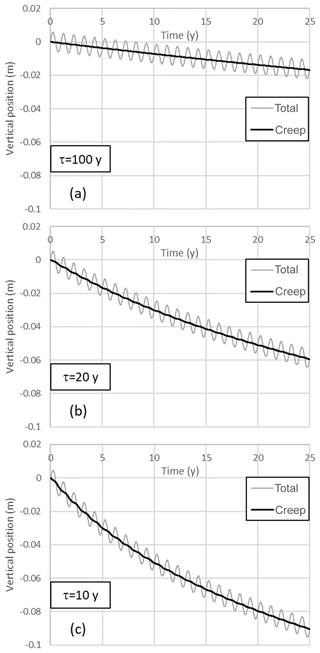
Figure 2 presents the calculated vertical land movement of the reference runs. τ values of 100, 20 and 10 years yield initial subsidence rates of about 1, 3 and 5 mm yr⁻¹, respectively. The total movement includes oscillations with an amplitude of about 5 mm that are predominantly caused by the elastic response of the peat and the clay to the seasonal stress changes. The accumulated irreversible, inelastic subsidence is labelled “creep”. It includes subtle seasonal variations indicating that the creep rate accelerates (with some delay) when the water table declines and decelerates when the water table rises.

Figure 2 Calculated subsidence for the reference runs.

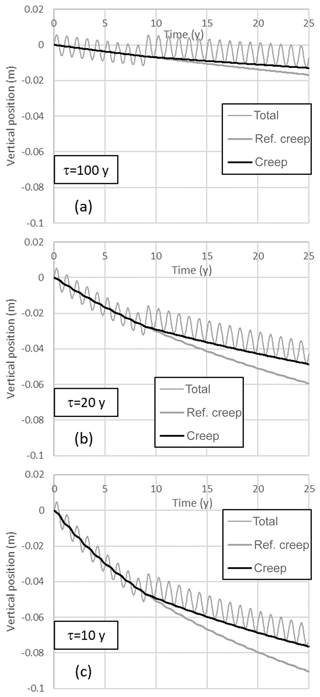
Figures 3–5 present the calculated vertical land movement for the three water table scenarios. To visualize the impact of the changed conditions, the creep component of the reference runs (Fig. 2) is shown for reference.

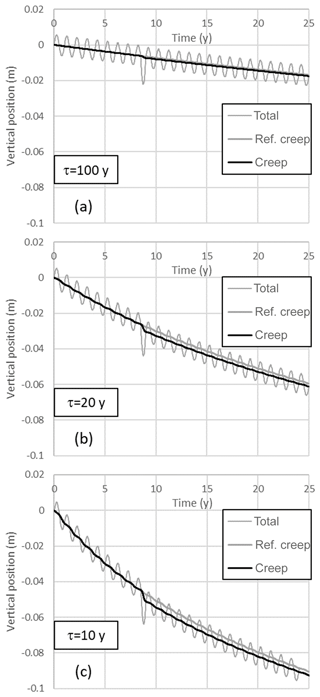
Figure 3 Calculated subsidence for scenario “dry summer”. The creep of the reference runs is depicted as “ref. creep”.

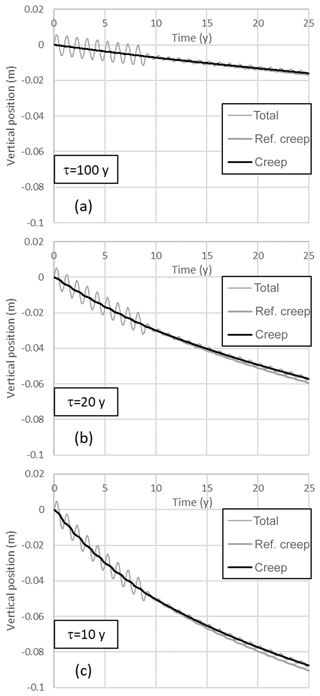
Figure 4 Calculated subsidence for scenario “damping”. The creep of the reference runs is depicted as “ref. creep”.

Figure 5 Calculated subsidence for scenario “raising”. The creep of the reference runs is depicted as “ref. creep”.

4 Discussion and conclusions

4.1 Elucidation of results of the scenarios

4.1.1 Drought scenario

Figure 3 shows that a single dry season with 1 m extra water table lowering, has a distinct subsidence impact (up to about 1 cm). However, most of this subsidence is due to elastic deformation and is recovered by the end of the drought. The net impact of the drought – defined here by the difference between the “creep” and “ref. creep” curves – is induced by enhancement of the rate of creep during the period in which the water table is anomalously low. The duration of this period (6 months in the simulation), therefore, is an important factor that determines the magnitude of the post-drought impact. The results further show that the impact is more significant for low values of τ (low OCR and high background subsidence rate). Furthermore, the loading and unloading caused by the drought and its recovery leaves the peat and clay mildly overconsolidated after the drought. That is, the OCR is slightly enhanced, and the creep rate slightly reduced after the drought. This is visible in Fig. 3c where the “creep” and “ref. creep” curve very slowly converge over the years after the drought. The net impact of the drought is very small relative to the background subsidence.

4.1.2 Damping scenario

The reduction of the amplitude of seasonal water table variation by 0.4 m (80 %) moderates the seasonal variation of the total land surface movement by approximately the same amount, and the annual average creep rate is slightly reduced (Fig. 4). The impact of the latter, in terms of millimetres of subsidence prevented, takes many years to decades to develop. The reduction of the annual creep rate is the result of opposing contributions of the wet and the dry season. The raised water table during the dry period compared to the reference condition, reduces the creep rate in that season. However, during the wet season, the lower water table compared to the reference condition enhances the creep rate during that time. The contribution of the dry season prevails in the net impact. This indicates that the effectiveness would be larger if only the dry season water table would be raised, and the wet season water table would be left untouched. The net impact of the drought is very small relative to the background subsidence.

4.1.3 Raising scenario

The permanent increase of the mean water table by 0.4 m has both a direct and a secular effect on the land surface elevation (Fig. 5). The direct effect consists of elastic uplift/heave of about 5 mm. The secular effect consists of the reduction of the creep rate. The reduction of the creep rate is permanent and applies to both the wet and the dry season (the amplitude of water table variation is not modified in this scenario). Comparison with Figs. 3 and 4 reveals that the impact of permanently raising of the water table is larger than for the other two scenarios. The greater impact is due to the permanent reduction of the creep rate. However, since water tables are already maintained at rather shallow depth in parts of The Netherlands that contain Holocene soft-soils, localities where water table can be raised by several decimetres or more without causing damage are probably very limited.

4.2 Need for field- and laboratory testing

The isotache model employed in this study, includes modern-day concepts of the soil mechanics of Holocene peat and clay. This model has been developed for the modelling of, and is primarily tested against, settlement caused by large loads such as dikes, and surcharge that is applied in areas where new residential areas are being built. It is presently unclear to what extent the model also accurately represents creep rates and creep behaviour for the small loads associated with the water table scenarios considered in this manuscript. Dedicated field- and laboratory tests are needed to shed more light on creep rates and creep behaviour for effective stress levels at or below the preconsolidation stress, and to test the validity of presented results.

4.3 Conclusions

Modelling employing an isotache-based viscoelastic compression model adopted from certified geotechnical software for settlement modelling allows quantitative assessment of the subsidence impact of interferences in water table conditions in urban areas.

Model results indicate that:

• The absolute subsidence impact of measures increases with increasing background subsidence rate.

• The effectiveness of measures increases with the duration of the period during which water tables are raised. That is, permanent raising tends to be more effective than periodic or occasional prevention of water table drops.

• For conditions that exist in urban areas in The Netherlands, water table interventions are predicted to prevent a fraction of the subsidence that would have occurred without the intervention.