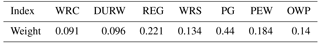The use of an integrated variable fuzzy sets in water resources management

Based on the evaluation of the present situation of water resources and the development of water conservancy projects and social economy, optimal allocation of regional water resources presents an increasing need in the water resources management. Meanwhile it is also the most effective way to promote the harmonic relationship between human and water. In view of the own limitations of the traditional evaluations of which always choose a single index model using in optimal allocation of regional water resources, on the basis of the theory of variable fuzzy sets (VFS) and system dynamics (SD), an integrated variable fuzzy sets model (IVFS) is proposed to address dynamically complex problems in regional water resources management in this paper. The model is applied to evaluate the level of the optimal allocation of regional water resources of Zoucheng in China. Results show that the level of allocation schemes of water resources ranging from 2.5 to 3.5, generally showing a trend of lower level. To achieve optimal regional management of water resources, this model conveys a certain degree of accessing water resources management, which prominently improve the authentic assessment of water resources management by using the eigenvector of level H.

1 Introduction

Regional rational allocation of water resources means to perform rational allocation of water resources available in the region by various means following certain principles and corresponding criteria (Wang et al., 2008). With the improvement achieved in water resources development and utilization, China has performed water allocation based on macroscopic economy, ecological water consumption and reservoir regulation etc. successively, and realized water allocation-based channel water quality distribution; water resource allocation played a vital role in guiding the rational utilization of water resources and the rapid social and economic development in China during the implementation of the Tenth Five-year Plan, the Eleventh Five-year Plan, and the Twelfth Five-year Plan (Wang and You, 2008; Wang et al., 2008). Due to the aged urban water facilities and the rural water consumption that was difficult to make statistics of in the past, industrial water utilization was far from being consistent with the most stringent system of water resources management; with the update and perfection of urban pipe network facilities, the significant improvement of rural water facilities, and the enhancement of water resources development and utilization in the northern part of China in recent years, it's essential to further improve the water resources management measures to achieve the development of industrial structure featuring “industry determination by water”; in view of the current water resources development and utilization, dynamic industrial water allocation should be a major measure for management improvement.

With Zoucheng County as an example, this paper analyzes and predicts the water consumption structure and water consumption level of Zoucheng County in the future level year through system dynamics model (SD), builds and evaluates the water use index system for the planned level year using variable fuzzy set evaluation model (VFS), performs qualitative and quantitative analysis of the water resources consumption and the extent to which water supports social and economic development in Zoucheng County, and proposes the measures for improving water resource management in Zoucheng County based on evaluation result.

2 Theory and methodology

2.1 System dynamics (SD) model

System dynamics (SD) model suits for the management of modern social system since it's based on OP and control theory. SD model divides the research object into a number of subsystems, establishes the cause-and-effect network between subsystems based on the information feedback mechanism in each subsystem, and probes into the relationship between the whole and subsystems, and between subsystems (Rehan et al., 2013). As well , SD model was applied as a decision support tool to evaluate and analyze ingapore's integrated water resources. The results shows it is a useful support tool for deciding sustainable water resources (Xi and Poh, 2013). In nature, SD model is a first order differential equation group that describes the dependence of the variation rate of each state variable in the system on state variables or certain inputs etc., further takes into account some factors contributing to the change of state variables, and resolves the description of variation rate into the description of some flow rates based on the actual conditions of system and the research requirements. Mathematical equation of SD model (Simonovic and Fahmy, 1999):

1. State variable: Input and output variables or the variables accumulated by either thereof.

   $$\begin{array}{}\text{(1)}& L_k=L_j+\text{DT}\left({\text{IR}}_{jk}-{\text{OR}}_{jk}\right)\end{array}$$

   Where, L_k, R_jk-Output and input rates (variation rate);

   DT-Time interval.

2. Rate equation: Input and output parallel variable.

   $$\begin{array}{}\text{(2)}& {\displaystyle \frac{L_k-L_j}{\text{DT}}}={\displaystyle \frac{\text{DL}}{\text{DT}}}={\text{IR}}_{jk}-{\text{OR}}_{jk}\end{array}$$

3. Auxiliary equation:

   In SD model, the algebra of rate equation requires additional algebraic calculation, i.e. auxiliary equation. It can be used to solve the problems of nonlinear, high order and complex time-varying systems. It can accurately understand and show the relationship between internal and external factors.

4. Table function:

   Since simple algebraic combination-based auxiliary variable can't accurately describe nonlinear relationship, graphical representation of non-liner function is needed, i.e. through table function.

System dynamics method features fast analysis and simple model building, as well as the use of non-linear equation, but this in turn represents the weakness of system dynamics: Even a tiny perturbation of nonlinear equation parameters that describe the intrinsic relation of system may bring about the absurdity of long-term analysis result. A novel integrated decision support tool, which synergized System Dynamics (SD) and Analytic Hierarchy Process (AHP) was proposed in Singapore's sources of water supply, shows that the limited capacity and long construction time of underground water have a profound impact on Singapore's water resources (Xi and Poh, 2015). As well, variable set fuzzy evaluation is suitable for the study on complex system since it gives overall evaluation of objectives constrained by various factors using fuzzy mathematics as its theoretical basis, thereby giving a quantitative description of water resources bearing capacity; furthermore, variable set fuzzy evaluation can be used with scenario analysis to provide decision makers with technical support.

2.2 Variable fuzzy sets (VFS)

Defining the concept of VFS, we set that U is a fuzzy concept, A and Ac reflect the attractability and repellency respectively. To any elements u (u∈U), μ_A and μ_Ac are the relative membership function of element u to A and Ac that express the degrees of attractability and repellency (Chen, 2012, 2013; Wang et al., 2014).

$$\begin{array}{}\text{(3)}& {\displaystyle }{\mathit{\mu }}_A+{\mathit{\mu }}_{\text{Ac}}=\mathrm{1},\mathrm{0}\le {\mathit{\mu }}_A\le \mathrm{1},\mathrm{0}\le {\mathit{\mu }}_{\text{Ac}}\le \mathrm{1}\end{array}$$

Where, μA is defined as relative difference degree u to A.

Suppose the regional water resources utilized level has m indices eigenvalue as follows:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{I}_{ab}=\left[\begin{array}{cccc}[a_{\mathrm{11}},b_{\mathrm{11}}]& [a_{\mathrm{12}},b_{\mathrm{12}}]& \mathrm{\dots }& [a_{\mathrm{1}c},b_{\mathrm{1}c}]\\ [a_{\mathrm{21}},b_{\mathrm{21}}]& [a_{\mathrm{22}},b_{\mathrm{22}}]& \mathrm{\dots }& [a_{\mathrm{2}c},b_{\mathrm{2}c}]\\ \mathrm{⋮}& \mathrm{⋮}& \mathrm{\dots }& \mathrm{⋮}\\ [a_{m\mathrm{1}},b_{m\mathrm{1}}]& [a_{m\mathrm{2}},b_{m\mathrm{2}}]& \mathrm{\dots }& [a_{mc},b_{mc}]\end{array}\right]\\ \text{(4)}& {\displaystyle }& {\displaystyle }=\left(\left[a_{ih},b_{ih}\right]\right)\end{array}$$

Where, I_ab represents the index function; a means the index; b stands for the index level.

First, the subjective weight of index is determined through analytic hierarchy process; then, entropy method is used to obtain the expert weight entropy model based on the pairwise discrimination matrices established by experts for evaluating the quality of information presented by experts; finally, combination is performed to figure out the index fusion weight.

$$\begin{array}{}\text{(5)}& W=\sum _{j=\mathrm{1}}^m{w}_j\times S\left(j=\mathrm{1},\mathrm{2},\mathrm{\cdots },m\right)\end{array}$$

Where, W means the final fusion weight; w_j represents the index weight proposed by each expert; S stands for expert's weight.

Integrated relative membership degree vector of the scheme for Level h:

$$\begin{array}{}\text{(6)}& V_h\left(u_j\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{1}+\left\{\left.\frac{\sum _{i=\mathrm{1}}^m\left[w_i\right(\mathrm{1}-{\mathit{\mu }}_{ih}\left(u_j\right)){]}^p}{\sum _{i=\mathrm{1}}^m\left[w_i{\mathit{\mu }}_{ih}\right(u_j){]}^p}\right\}\right.}}\end{array}$$

Where, V_h (u_j) represents the relative membership degree of each index of Scheme j for Level h; w_i means the weight of index i, while $w_{\mathrm{1}}+w_{\mathrm{2}}+\mathrm{\dots }{w}_m=\mathrm{1}$; α=1, and p represents distance parameter: In this paper, Hamming distance p=1 is assumed to achieve a linear model of integrated relative membership degree of the scheme for Level h, namely

$$\begin{array}{}\text{(7)}& V_h\left(u_j\right)=\sum _{i=\mathrm{1}}^m{w}_i{\mathit{\mu }}_{ih}\left(u_j\right)\end{array}$$

Since the distribution sequence of relative membership degree of u for Level C in the domain of discourse and the Weight h of Variable c are given, their sum is called “the eigenvalue of level variable”:

$$\begin{array}{}\text{(8)}& H_{\left(u\right)}=\sum _{h=\mathrm{1}}^c{\mathit{\mu }}_A\left(u_o\right)h\end{array}$$

2.3 Integrated variable fuzzy sets model (IVFS)

System dynamics (SD) model works out the water allocation that reflects the present regional situation and future industrial structure through the establishment of water use index system; the variable fuzzy sets choose the evaluation index system that reflect water consumption level, compute the water resource utilization level eigenvalue, and identify the focus of regional water allocation and management in future based on eigenvalue variation analysis. IVFS is relatively low in parameter accuracy and pays more attention to dynamic behavior and system structure.

3 Case study

3.1 water utilization in the index system

Located in Jining, Shandong Province, Zoucheng County is one of top 100 counties in China. Industry-specific water consumption in Zoucheng County in 2015: The per capita water consumption was 256.93 m³ a⁻¹, approx. 1/2 of the per capita water consumption in China; the water consumption per RMB 10 000 of industrial GDP amounted to 15.71 m³, approx. 1/8 of the national average; the urban domestic water consumption was 106 L p⁻¹ d, approx. 1/2 of the national average; the rural residents' living water consumption was 83 L p⁻¹ d, which was approximately equal to the national average; the water consumption per Mu of farmland irrigated was 258 m³, approx. 1/2 of the national average. Taken together, Zoucheng County leads in China in terms of water utilization.

In order to suit the comparison for the performance of this approach, evaluated index system is chosen to keep in line with the regional actual situation. In this paper, a series of indices are chosen to input SD model in Table 1 which can be divided into two types according to the status of the index: one is a constant and the other change with the function.

Table 1 The regional variable of evaluating index system for Zoucheng.

After the system dynamics model to calculate the region water resources allocation, according to the actual area analysis, analysis level indicators of water resources, and according to the analysis of regional water level change management. From the output of SD model, this paper Selects the evaluation index: water resources per capita (WRC) (m³), development and utilization rate of water resources (DURW) (%), regional economic growth rate (REG) (%), water shortage ratio (WRS) (%), per-10000-yuan-GDP water (PG) (m³), proportion of ecological water (%) (PEW), overlimit rate of water pollution (OWP) (%).

Table 2 The evaluation index system based on VFS.

3.2 Water level based on the IVFS

According to the SD model analysis, matrix I_ab can be determined as follows.

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathbf{I}}_{ab}=\\ {\displaystyle }& {\displaystyle }\left[\begin{array}{ccccc}[\mathrm{550},\mathrm{450}]& [\mathrm{450},\mathrm{350}]& [\mathrm{350},\mathrm{250}]& [\mathrm{250},\mathrm{150}]& \left[\mathrm{150.50}\right]\\ [\mathrm{0.55},\mathrm{0.6}]& [\mathrm{0.6},\mathrm{0.65}]& \left[\mathrm{0.65.0.7}\right]& [\mathrm{0.7},\mathrm{0.75}]& [\mathrm{0.75},\mathrm{0.8}]\\ [\mathrm{11},\mathrm{10}]& [\mathrm{10},\mathrm{9}]& [\mathrm{9},\mathrm{8}]& [\mathrm{7},\mathrm{6}]& [\mathrm{5},\mathrm{4}]\\ [\mathrm{0},\mathrm{0.03}]& [\mathrm{0.03},\mathrm{0.06}]& [\mathrm{0.06},\mathrm{0.09}]& [\mathrm{0.09},\mathrm{0.12}]& [\mathrm{0.12},\mathrm{0.15}]\\ [\mathrm{10},\mathrm{12}]& [\mathrm{12},\mathrm{14}]& [\mathrm{14},\mathrm{16}]& [\mathrm{16},\mathrm{18}]& [\mathrm{18},\mathrm{20}]\\ [\mathrm{0.5},\mathrm{0.48}]& [\mathrm{0.48},\mathrm{0.46}]& [\mathrm{0.46},\mathrm{0.44}]& \left[\mathrm{0.44.0.42}\right]& [\mathrm{0.42},\mathrm{0.4}]\\ [\mathrm{0},\mathrm{0.1}]& [\mathrm{0.1},\mathrm{0.2}]& [\mathrm{0.2},\mathrm{0.3}]& [\mathrm{0.3},\mathrm{0.4}]& [\mathrm{0.4},\mathrm{0.5}]\end{array}\right]\end{array}$$

In order to ensure the consistency of region, this article selects AHP and entropy method to build the index weight (Yu et al., 2009)

Table 3 The weights of indices by AHP and Entropy Model.

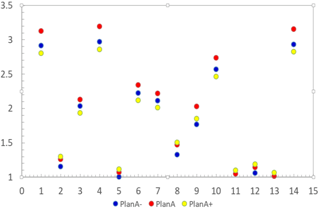
In consideration of clear expression, this paper order the town of Zoucheng: Chengqu, Xiangcheng, Chengqian, Dasu, Beishu, Zhongxindian, Tangcun, Taiping, Shiqiang, Zeshan, Kanzhuang, Zhangzhuang,Taihuang and Guoli from 1 to 14.

Figure 1 The Water Utilization level of Each town

As Fig. 1 shows the water level of each town in Zoucheng performs a big changes, mainly because the present situation of towns economy, and the regional water resources utilized level. As well, these towns which get a higher water level shows an order of Plan A, Plan A−, Plan A+. This implies that, although the water level level is higher, but these towns already present a full capacity. These towns that get a low water level, are still has certain development potential.

4 Conclusions

According to the model output result:

• a.

  The water resources consumption of Zoucheng County in current and planned level years presents an increasing trend; the consumption will increase fast between current year and 2020 (short-range planned level year), and increase slowly between 2020 and 2030 (long-term planned level year), which conforms to the overall development trend of Zoucheng County. The variation of growth rate mainly results from the fact that the high water consumption in Zoucheng County narrows its growth potential.

• b.

  In Zoucheng County, the water consumption is high in urban area and its surroundings, and at general level in remote towns, which reflects that fact that the water consumption decreases with the increase of the percentage of agricultural water; in consideration of the overall industrial layout and rural population in Zoucheng County, a threshold for agricultural water shall be defined for water resource management in the future.

It can be concluded that the evaluation of Water resources using settings can play a part in water management. These conclusions can guide decision makers and government in future considerations related to water-lack management in regional development.